Abstract
Therapeutic proteins (TPs) have ranked among the most important and fastest-growing classes of drugs in the clinic, yet the development of successful TPs is often limited by unsatisfactory efficacy. Understanding pharmacokinetic (PK) characteristics of TPs is key to achieving sufficient and prolonged exposure at the site of action, which is a prerequisite for eliciting desired pharmacological effects. PK modeling represents a powerful tool to investigate factors governing in vivo disposition of TPs. In this mini-review, we discuss many state-of-the-art models that recapitulate critical processes in each of the absorption, distribution, metabolism/catabolism, and excretion pathways of TPs, which can be integrated into the physiologically-based pharmacokinetic framework. Additionally, we provide our perspectives on current opportunities and challenges for evolving the PK models to accelerate the discovery and development of safe and efficacious TPs.
SIGNIFICANCE STATEMENT This minireview provides an overview of mechanistic pharmacokinetic (PK) models developed to characterize absorption, distribution, metabolism, and elimination (ADME) properties of therapeutic proteins (TPs), which can support model-informed discovery and development of TPs. As the next-generation of TPs with diverse physicochemical properties and mechanism-of-action are being developed rapidly, there is an urgent need to better understand the determinants for the ADME of TPs and evolve existing platform PK models to facilitate successful bench-to-bedside translation of these promising drug molecules.
Introduction
With the development of the recombinant DNA technology, therapeutic proteins (TPs) have revolutionized treatments for a multitude of diseases and steadily accounted for 50%–60% of the top 10 best-selling drugs worldwide in recent years (Urquhart, 2021). Marketed TPs encompass monoclonal antibodies (mAbs), antibody fragments, enzymes, hormones, growth factors, cytokines, fragment crystallizable (Fc)-fusion proteins, and antibody-drug conjugates (ADCs) (Lagasse et al., 2017). MAbs represent the dominant and the fastest-growing class of TPs in the pipeline, with the 100th mAb approved just recently (Mullard, 2021). Despite their therapeutic potential, TPs have low success rates in clinical development, with only about 1 in 10 molecules in phase 1 studies approved by the US Food and Drug Administration (Hay et al., 2014). This has been largely attributed to the failure to show significant improvement in the efficacy compared with the placebo group or existing treatments at the clinically tolerated doses of TPs (Arrowsmith, 2011). Although target validation for the chosen indications is vital for the success of TPs (Morgan et al., 2012), sufficient drug exposure at the site of action is a prerequisite for eliciting desired pharmacodynamic (PD) effects, which underscores the importance of understanding the pharmacokinetic (PK) characteristics of TPs. Previous experience with the development of small molecule drugs has suggested that appreciation and research of drug metabolism and PK significantly reduces failures of drug candidates associated with undesired PK characteristics in clinical trials (Kola and Landis, 2004), and we may be witnessing such a transition in the field of TPs as well.
Because of the large size, high polarity, and high affinity of TPs, they differ substantially from traditional small molecule drugs in absorption, distribution, metabolism, and excretion (ADME) pathways (for comprehensive reviews on PK/PD properties of TPs, readers are referred to Lobo et al., 2004; Wang et al., 2008; Vugmeyster et al., 2012; Conner et al., 2020). Unlike many small molecules that display good gastrointestinal absorption, TPs are too large to cross the intestinal membrane and subject to proteolytic degradation in the gut. Therefore, TPs are typically administered via parenteral routes. Distribution of TPs is relatively restricted to the vascular and interstitial spaces, and the tissue concentration is not in rapid equilibrium with that in the plasma. Although small molecule drugs are most commonly eliminated through hepatic metabolism and renal and biliary excretion (Wienkers and Heath, 2005), TPs can be cleared via catabolism in the lysosome following nonspecific pinocytosis or receptor-mediated endocytosis, resulting in small peptides or amino acids that are unlikely to be pharmacologically active or toxic (Shah, 2015). Intracellular catabolism may be circumvented by the interaction between the Fc moiety of TPs and the neonatal Fc receptor (FcRn), which explains the unusually long half-life of mAbs. For TPs with a molecular weight (MW) less than around 60 kDa, renal excretion also represents an important elimination pathway (Meibohm and Zhou, 2012). Nonlinearity in the PK of TPs is not associated with small molecule transporters, metabolic enzymes, or plasma protein binding but frequently attributed to saturable target binding or Fc receptor binding (Ferl et al., 2016).
The distinct ADME features of TPs have aroused many mathematical models to characterize the PK of these molecules. In fact, PK modeling is integral to the drug development and clinical applications of TPs as it supports candidate selection and guides protein engineering strategies in the discovery phase and facilitates clinical translation and optimization of dosing regimens in the clinic. In this mini-review, we provide a brief overview of the PK models that can simultaneously characterize ADME processes of TPs and elaborate on mechanistic submodels that can characterize key distribution, elimination, and absorption processes for TPs. Additionally, we conclude with a discussion on outstanding challenges for modeling the PK of TPs.
Types of PK Models to Characterize the ADME Processes of TPs
The most parsimonious PK model for TPs may be a classic two-compartment model with linear and/or nonlinear clearance. This model appears adequate for recapitulating PK profiles of TPs on many occasions, despite that the assumption underlying the mammillary models (i.e., the elimination of the drug only occurs from the central compartment) does not hold for the majority of TPs. This data-driven model mainly finds use in population PK analysis (Ng et al., 2005) or in PK/PD modeling when the plasma PK is used to drive the PD model (Gibiansky and Frey, 2012).
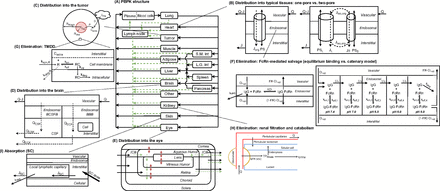
On the other hand, physiologically-based pharmacokinetic (PBPK) models represent the most complex and mechanistic mathematical framework to characterize ADME of TPs. A typical PBPK model consists of compartments representing various organs connected via blood and lymphatic flows in an anatomic manner (Fig. 1A). Each organ is further divided into vascular, endosomal, interstitial, and cellular spaces, where TP disposition is explicitly defined using physiologic processes as building blocks. PBPK models offer significant advantages over compartmental models. They yield TP concentrations and receptor occupancy in specific organs, allowing the development of reliable exposure-efficacy and exposure-toxicity relationships. The physiologic nature of PBPK models also enables robust and reliable interspecies scaling and prediction of PK, which is sometimes challenging using traditional allometric scaling as different species have different target expression profiles, target binding, and FcRn binding affinities. Since the development of the first PBPK model for mAbs and antibody fragments by Covell et al. (1986), PBPK models have evolved and expanded to incorporate up-to-date knowledge of physiology and TPs’ disposition characteristics. These include molecular size-dependent distribution and elimination (Baxter et al., 1994), target turnover and binding (Baxter et al., 1994), FcRn-mediated recycling (Ferl et al., 2005; Garg and Balthasar, 2007), and interspecies scaling (Baxter et al., 1995; Shah and Betts, 2012). One should be aware that many physiologic parameter values used for various species are collected from diverse resources or scaled/assumed (Shah and Betts, 2012). Boswell and colleagues published a series of work that measured organ vascular and interstitial volumes, and organ blood flow rates for rodents and monkeys, using consistent experimental techniques (Boswell et al., 2011; Boswell et al., 2014; Mandikian et al., 2018). It would be of importance to evaluate how these different physiologic parameter values impact the performance of TP PBPK models.
Schematic of ADME models for TPs. (A) Structure of a whole-body PBPK model for TPs’ disposition (adapted from Shah and Betts, 2012). Organs are represented by rectangular compartments connected via blood flows (solid arrows) and lymphatic flows (dashed arrows). Organ-specific distribution or elimination mechanisms will be elaborated below for tumor, brain, eye, kidney, and skin. (B) Diagram of tissue-level models that characterize distribution of TPs for a typical organ (adapted from Sepp et al., 2019), based on one-pore (left panel) or two-pore (right panel) theories. A tissue is divided into vascular, endosomal, and interstitial spaces. Diffusion is denoted by solid arrows and convection by dashed arrows. Specially curved arrows stand for the isogravimetric flow. (C) Representation of the Krogh cylinder tumor model (adapted from Cilliers et al., 2016). The area in red refers to tumoral vasculature, from where TPs can escape via diffusion. Transport of TPs can also be driven by surface uptake from an adjacent organ. (D) Structure of the brain PBPK model. Brain is divided into vascular, BCSFB, BBB, CSF, and parenchymal compartments. (E) Structure of the ocular PBPK model. Regions in the eye include cornea, ICB, lens, retina, choroid, sclera, aqueous humor, and vitreous humor. Black solid arrows represent blood flows, green dashed arrows represent convective flows, and red double-headed arrows represent diffusion processes. (F) Representation of endosomal models that characterize FcRn interaction with IgGs (adapted from Chen and Balthasar, 2012). The panel on the left-hand side assumes equilibrium binding between IgGs and FcRn. The panel on the right-hand side adopts a catenary model, where endosomal subcompartments have pH ranging from 7.4 to 6.0. (G) Representation of a TMDD model for a membrane-bound antigen in the tumor compartment. The free receptor has its inherent turnover rate and is allowed to bind to TPs in the extracellular space of a solid tumor. (H) Schematic of renal elimination of TPs (adapted from Rabkin and Dahl, 1993). Following glomerular filtration, TPs are internalized into tubular cells for degradation or eliminated into the urine. TPs in the postglomerular peritubular capillaries can also be endocytosed, followed by intracellular degradation. (I) Structure of a SC absorption model (adapted from Hu and D'Argenio, 2020). ICB, iris-ciliary body; L.G., int large intestine; SC, subcutaneous; S.M., small intestine.
One way to get around the complex parameterization of a full PBPK model is to employ a minimal PBPK (mPBPK) model, in which tissues are lumped into tight (muscle, skin, adipose, and brain) or leaky (other tissues) compartments based on vasculature and permeability, and the major distribution/elimination pathways are grouped accordingly (Cao et al., 2013). This simplified model still provides physiologically meaningful parameters when only plasma data are available and also has the potential of delineating disposition in tissues of interest by separating out a specific tissue compartment (Chen et al., 2018).
Going forward in this manuscript, we will highlight various models describing ADME processes of TPs, mostly in the context of the PBPK framework, as these models provide the most in-depth and accurate representations of underlying mechanisms and can be readily embedded into a mPBPK framework or linked to a compartmental model after simplification.
Models to Characterize Distribution of TPs
Transcapillary Transport: One-Pore Versus Two-Pore
Although small molecules can enter tissues readily via processes like transcellular diffusion and transporter-mediated uptake, extravasation of TPs is mostly restricted to diffusion and convection through paracellular pores of vascular endothelial wall (Fig. 1B). This process can be mathematically formulated as (Bresler and Groome, 1981):
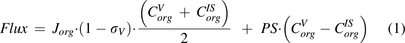
Where 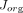 is the organ lymph flow,
is the organ lymph flow, 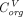 and
and 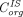 are vascular and interstitial concentrations of a tissue, and
are vascular and interstitial concentrations of a tissue, and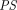 is the permeability-surface area product.
is the permeability-surface area product. 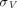 is the tissue vascular reflection coefficient, which represents the fraction of a solute that is unable to cross the pores. Typically,
is the tissue vascular reflection coefficient, which represents the fraction of a solute that is unable to cross the pores. Typically, 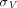 is greater (i.e., higher resistance) for larger-size proteins (Covell et al., 1986) and tissues with less leaky vasculature (Shah and Betts, 2012). For TPs as large as mAbs (150 kDa), the transcapillary transport is considered almost entirely convective (Baxter et al., 1995), and thus the flux from vascular space to interstitial space can be reduced to
is greater (i.e., higher resistance) for larger-size proteins (Covell et al., 1986) and tissues with less leaky vasculature (Shah and Betts, 2012). For TPs as large as mAbs (150 kDa), the transcapillary transport is considered almost entirely convective (Baxter et al., 1995), and thus the flux from vascular space to interstitial space can be reduced to 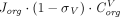 . Similarly, the mass transport from interstitial fluid to lymphatics is described as
. Similarly, the mass transport from interstitial fluid to lymphatics is described as 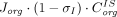 , where
, where 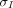 is the lymphatic reflection coefficient. One crucial assumption underlying these equations is that the pores have a uniform size (homoporosity, or one-pore model), which contradicts the actual physiology.
is the lymphatic reflection coefficient. One crucial assumption underlying these equations is that the pores have a uniform size (homoporosity, or one-pore model), which contradicts the actual physiology.
The two-pore phenomenon was first noted in the 1950s (Grotte, 1956) and further elaborated and mathematically formulated by Rippe and Haraldsson (1987, 1994). Continuous and fenestrated endothelium is assumed to contain two categories of pores, small pores (radius  = 4.44 nm) and large pores (radius
= 4.44 nm) and large pores (radius 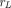 = 22.85 nm), and protein solutes extravasate by diffusion or convection via both types of pores (Fig. 1B). What makes the two-pore framework distinct from the one-pore model is the incorporation of isogravimetric flow (
= 22.85 nm), and protein solutes extravasate by diffusion or convection via both types of pores (Fig. 1B). What makes the two-pore framework distinct from the one-pore model is the incorporation of isogravimetric flow (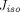 ), a circulation flow entering large pores and existing small pores, which can explain a transvascular flux of proteins even in the absence of net filtration (“isogravimetric” state). Accordingly, the actual lymph flows through these pores corrected for
), a circulation flow entering large pores and existing small pores, which can explain a transvascular flux of proteins even in the absence of net filtration (“isogravimetric” state). Accordingly, the actual lymph flows through these pores corrected for 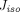 are:
are:
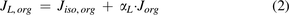
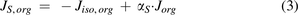
Where 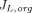 and
and 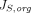 are organ lymph flows through large and small pores,
are organ lymph flows through large and small pores, 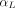 and
and 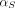 are relative abundance of both pores, and
are relative abundance of both pores, and 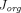 is the net organ lymph flow. Thus, both diffusive and convective processes for protein extravasation can be characterized in the clearance terms as below:
is the net organ lymph flow. Thus, both diffusive and convective processes for protein extravasation can be characterized in the clearance terms as below:
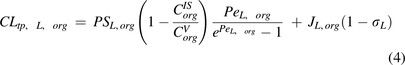
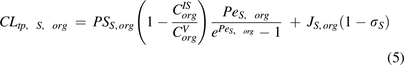
 and
and 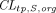 are transcapillary clearances through large and small pores in an organ,
are transcapillary clearances through large and small pores in an organ, 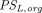 and
and 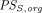 are the permeability-surface area products, and
are the permeability-surface area products, and 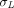 and
and 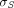 are vascular reflection coefficients. Particularly,
are vascular reflection coefficients. Particularly, 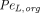 and
and 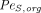 are the Peclet numbers that reflect the importance of convection versus diffusion in the extravasation process and defined as:
are the Peclet numbers that reflect the importance of convection versus diffusion in the extravasation process and defined as:
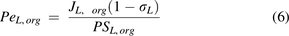
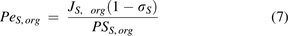
The two-pore formalism has been applied in PBPK models developed for antibodies and antibody fragments since 1994 (Baxter et al., 1994). Early work typically estimated values of certain key parameters, such as 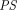 ,
,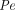 ,
, 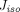 , and
σ (Baxter et al., 1994; Ferl et al., 2005; Davda et al., 2008) as they are difficult to measure and can vary depending on drugs and organs. Unfortunately, these parameter estimates differ substantially between studies and are often associated with high uncertainty and poor identifiability, restricting extensive utilization of the two-pore model. Sepp et al. mathematically derived
, and
σ (Baxter et al., 1994; Ferl et al., 2005; Davda et al., 2008) as they are difficult to measure and can vary depending on drugs and organs. Unfortunately, these parameter estimates differ substantially between studies and are often associated with high uncertainty and poor identifiability, restricting extensive utilization of the two-pore model. Sepp et al. mathematically derived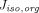 and
and 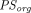 and found that they can be expressed as explicit linear functions of
and found that they can be expressed as explicit linear functions of 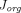 . Additionally, they also reported that
. Additionally, they also reported that 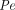 could be calculated using an empirical equation for
could be calculated using an empirical equation for 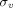 (Sepp et al., 2015). Due to these derivations, their model greatly reduced the number of parameters fitted (only
(Sepp et al., 2015). Due to these derivations, their model greatly reduced the number of parameters fitted (only 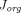 needed to be estimated for the two-pore extravasation) and could capture the whole-body PK of a nonbinding domain antibody. In pursuit of development of a generalized PBPK model to characterize a diverse array of TPs, Li and Shah (2019) further expressed glomerular sieving coefficient (discussed later),
needed to be estimated for the two-pore extravasation) and could capture the whole-body PK of a nonbinding domain antibody. In pursuit of development of a generalized PBPK model to characterize a diverse array of TPs, Li and Shah (2019) further expressed glomerular sieving coefficient (discussed later), 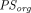 ,
,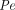 , and
σ as functions of MW so that the two-pore PBPK model could a priori predict the PK of eight TPs of different sizes without fitting any parameter and facilitate a better understanding of the contribution of diffusion and convection toward protein transport across a wide range of MW.
, and
σ as functions of MW so that the two-pore PBPK model could a priori predict the PK of eight TPs of different sizes without fitting any parameter and facilitate a better understanding of the contribution of diffusion and convection toward protein transport across a wide range of MW.
Special Tissues
In whole-body PBPK models, various tissues are usually treated as modules with similar kinetic processes. However, certain tissues differ significantly in terms of anatomy and physiology (e.g., solid tumor, brain, eye) and may require dedicated PK models for characterization of TP concentrations.
In solid tumors, deficient lymphatic drainage causes high interstitial hydrostatic pressure, which precludes convection of macromolecules. Meanwhile, the capillary wall tends to be more permeable than blood vessels in healthy tissues (Boucher et al., 1990). These features imply that extravasation of TPs is primarily dependent on diffusion. In addition, the solid tumor space can be viewed as a collection of Krogh cylinders, and TP distribution into the tumor can be described as:
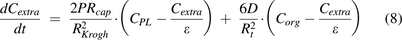
(Thurber et al., 2008; Schmidt and Wittrup, 2009; Thurber and Wittrup, 2012). The first term refers to protein permeation through the vascular capillary, and the second term indicates diffusion-driven uptake from the tumor surface that is in contact with the surrounding tissue (surface uptake), as shown in Fig. 1C. 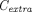 ,
, 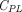 , and
, and 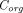 represent TP concentrations in the tumor extracellular space, the plasma, and the surrounding tissue.
P is the permeability coefficient across the capillary wall,
D is the diffusion coefficient,
ε is fraction of tumor that is accessible to macromolecules,
represent TP concentrations in the tumor extracellular space, the plasma, and the surrounding tissue.
P is the permeability coefficient across the capillary wall,
D is the diffusion coefficient,
ε is fraction of tumor that is accessible to macromolecules, 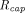 is the capillary radius,
is the capillary radius, 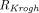 is half the average distance between blood vessels within the tumor, and
is half the average distance between blood vessels within the tumor, and 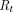 is tumor radius. It is apparent in the equation that the surface uptake pathway dominates when the tumor is small and less vascularized (i.e., small
is tumor radius. It is apparent in the equation that the surface uptake pathway dominates when the tumor is small and less vascularized (i.e., small 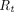 ), and the TP distribution occurs almost exclusively from extravasation when the tumor is larger and vasculature is well developed. Schmidt and Wittrup also derived empirical relationships between molecular size and
), and the TP distribution occurs almost exclusively from extravasation when the tumor is larger and vasculature is well developed. Schmidt and Wittrup also derived empirical relationships between molecular size and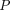 ,
D, and
ε by fitting a two-pore model of the capillary wall and a two-pore model of tumor interstitium using experimental data (Schmidt and Wittrup, 2009). These relationships not only help readily calculate tumor uptake for various TPs but also provide insights into the antigen binding affinity required for prolonged retention in the tumor for different-size TPs.
,
D, and
ε by fitting a two-pore model of the capillary wall and a two-pore model of tumor interstitium using experimental data (Schmidt and Wittrup, 2009). These relationships not only help readily calculate tumor uptake for various TPs but also provide insights into the antigen binding affinity required for prolonged retention in the tumor for different-size TPs.
In addition to extravasation into the tumor, heterogeneous intratumoral distribution is of great interest. The heterogeneity is often featured by perivascular distribution of TPs, leading to regions of antigen-positive cells completely untargeted. This phenomenon is attributed to the “binding site barrier,” which refers to high-affinity binding to the target (and subsequent degradation) right after extravasation of the TP preventing deeper distribution into the tumor (Fujimori et al., 1990). A few model structures have been proposed to delineate heterogeneous drug distribution within a tumor, with different levels of complexities. The Krogh cylinder model in conjunction with a PBPK framework has been capable of predicting antigen-bound fraction as a function of the distance from the vasculature and evaluating strategies to overcome the binding site barrier (Cilliers et al., 2016). Shah et al. proposed a spherical tumor model that contains five circular layers with equal thickness, with adjacent layers connected by permeability surface area coefficients (Shah et al., 2009). This model can be modified to characterize the binding site barrier by incorporating target expression and binding in each tumor layer (Glassman and Balthasar, 2019). The simplest approach is to allow only a fraction of tumor antigens to be accessible for binding (Urva et al., 2010), but the associated caveats are complete loss of information about the heterogeneity and poor generalizability of the fraction term when drug doses, binding affinities, or tumor sizes change.
The brain represents another challenging tissue to model as it is known to have a tight blood-brain barrier (BBB) and blood-cerebrospinal fluid barrier (BCSFB), and complex fluid flows in the central nervous system. A generic two-pore PBPK model in PK-Sim platform could fit antibody disposition data in mouse brain reasonably well, and the brain lymph flow and hydraulic conductivity were estimated to be extremely low (Niederalt et al., 2018). Adding a cerebrospinal fluid (CSF) flow exiting the brain that removes macromolecules can further reduce predicted brain exposures of TPs (Brinker et al., 2014; Sepp et al., 2019). Change et al. presented a higher spatial-resolution brain PBPK model that details paracellular transport and transcytosis through BCSFB and BBB, CSF compartmentalization (including lateral ventricle, third-fourth ventricle, cisterna magna, and subarachnoid space), and circulations of CSF and brain extracellular flow (Fig. 1D). This translational model was calibrated using rat disposition data in various brain regions and accurately predicted brain PK of mAbs in mice, monkeys, and humans (Chang et al., 2019).
As the research on eye diseases expands, ocular disposition is of more interest. The eye is characterized by delicate compartmentation, a variety of barriers, and complex fluid dynamics (Perez et al., 2013). Intravitreal dosing is the mainstream administration route in treating ocular disorders such as age-related macular degeneration and diabetic retinopathy, which requires frequent injections and causes pain. On the other hand, several anticancer mAbs and ADCs targeting diverse antigens have been shown to induce ocular toxicities following intravenous injections. As such, modeling drug exposures in the eye is valuable not only for prioritizing suitable TPs during drug development and optimization of dosing regimen but also for evaluating ocular toxicity potential. A novel anatomic ocular compartment that contains cornea, iris-ciliary body, aqueous humor, lens, vitreous humor, retina, choroid, and sclera, embedded in a PBPK framework, has been proposed to characterize ocular disposition following intravitreal or systemic administration (Bussing and Shah, 2020), as shown in Fig. 1E. Considering that current antivascular endothelial growth factor TPs for ocular diseases include IgG, Fc-fusion, antigen-binding fragment (Fab), and single-chain variable fragment formats, the two-pore formalism is anticipated to be incorporated in the ocular compartment to better characterize the ocular absorption and disposition processes.
Models to Characterize Catabolism and Excretion of TPs
TPs are typically eliminated by the following pathways: (1) target-mediated drug disposition, (2) nonspecific pinocytosis/endocytosis followed by intracellular catabolism (for larger TPs) throughout the body, (3) renal filtration (for smaller TPs), and (4) antidrug antibody (ADA)-induced clearance. In particular, FcRn-mediated salvage plays an important role in the disposition of mAbs and Fc-fusion proteins.
Interaction with FcRn
FcRn is known to be expressed in vascular endothelial cells of many tissues and hematopoietic cells and contribute to the long serum persistence of IgGs and albumin. Binding between IgGs and FcRn is pH-dependent, with high affinity at acidic pH and negligible binding at physiologic pH. Following fluid phase pinocytosis, IgG binds to FcRn upon acidification of endosomes. Unbound IgG is subject to lysosomal degradation, whereas FcRn-bound IgG is returned to apical or basolateral cell surface. Once exposed to the physiologic pH of extracellular fluid, IgG is released into the systemic circulation or the interstitial fluid.
The PBPK model by Ferl et al. was one of the first to account for FcRn expression in skin and muscle and incorporated IgG uptake into endothelia, IgG binding to FcRn, recycling of FcRn-bound IgG, and degradation of unbound IgG in the endosome (Ferl et al., 2005). The PBPK model proposed by Garg and Balthasar accounted for FcRn expression in all the tissues and characterized mAb PK in wild-type and FcRn-knockout mice (Garg and Balthasar, 2007). As shown in Fig. 1F, they assumed an equilibrium binding between mAb and FcRn in the endosomal space. Therefore, within the endosomal compartment, unbound IgG was expressed as a fraction (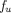 ) of total IgG, and
) of total IgG, and 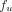 was defined as:
was defined as:
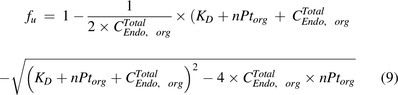
Above, 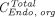 is the total endosomal IgG concentration in an organ,
is the total endosomal IgG concentration in an organ, 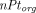 is the total FcRn concentration, and
is the total FcRn concentration, and 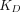 is the dissociation constant of the antibody for binding to FcRn. Compared with the model by Ferl, in this model the organ-specific FcRn capacity was assumed to be proportional to organ weight and adjusted based on total FcRn amount in the body. This model estimated the fraction of FcRn-bound antibody that recycles back to the vascular space (
is the dissociation constant of the antibody for binding to FcRn. Compared with the model by Ferl, in this model the organ-specific FcRn capacity was assumed to be proportional to organ weight and adjusted based on total FcRn amount in the body. This model estimated the fraction of FcRn-bound antibody that recycles back to the vascular space (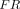 ) to be 0.715, and this value has been carried forward in many subsequent PBPK models. Nowadays, FcRn-mediated recycling is routinely incorporated within mAb PBPK models, with variable assumptions across models.
) to be 0.715, and this value has been carried forward in many subsequent PBPK models. Nowadays, FcRn-mediated recycling is routinely incorporated within mAb PBPK models, with variable assumptions across models.
Prompted by the fact that the equilibrium binding model over-predicts the improvement in antibody half-life with increasing equilibrium affinity of FcRn binding at pH 6, Chen and Balthasar (2012) constructed a catenary FcRn binding model that describes endosomal transit process, gradual acidification of endosomes, and kinetic binding between the antibody and FcRn. This was justified by the fact that residence time in endosomes (∼10.8 minute) is too short for the mAb-FcRn interaction to reach equilibrium (dissociation half-life of 6–58 minute). In this catenary model, the vascular endosomal space is subdivided into five transit compartments with pH of 7.4, 7.0, 6.5, 6.0, and 6.0, and the transit time (
τ) was determined to be 2.7 minute through each compartment (Fig. 1F). FcRn was allowed to interact with IgG using pH-dependent association rates (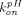 ) and dissociation rates (
) and dissociation rates (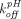 ) in each subcompartment, and only in the last subcompartment unbound IgG was assumed to be cleared and bound IgG was assumed to recycle. Of note, an underlying constraint between the tissue endosomal subcompartment volume (
) in each subcompartment, and only in the last subcompartment unbound IgG was assumed to be cleared and bound IgG was assumed to recycle. Of note, an underlying constraint between the tissue endosomal subcompartment volume (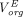 ) and uptake clearance (
) and uptake clearance (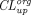 ) exists in this model to ensure endosomal volume homeostasis and FcRn and endogenous IgG steady-state:
) exists in this model to ensure endosomal volume homeostasis and FcRn and endogenous IgG steady-state:

Additionally, this model employs measured tissue-specific FcRn expression (Li and Balthasar, 2018), contrary to assuming a universal FcRn concentration across tissues in prior models (Urva et al., 2010; Shah and Betts, 2012). The equilibrium binding model performed as well as the catenary model in predicting PK of normal mAbs. However, the former predicts an almost proportional increase in mAb half-life with enhanced FcRn binding, whereas the latter predicts much more modest half-life extension, which is more consistent with observations reported in the literature (Chen and Balthasar, 2012).
In prior models, FcRn concentrations are assumed to be static (either tissue-specific or universal), which makes them inappropriate for characterizing PK of anti-FcRn mAbs used in treating autoimmune diseases as FcRn density is expected to be altered under the treatment. Accordingly, on top of the catenary model, Li and Balthasar (2019) took account of FcRn turnover by supplementing an FcRn pool compartment, where synthesis and degradation of FcRn can occur. This pool compartment provides the first endosomal subcompartment with FcRn and collects unbound and IgG-Fc–bound FcRn from the last endosomal subcompartment at a rate of  . Anti-FcRn mAbs are allowed to bind to FcRn through either the Fab arms or Fc region. In the last subcompartment, Fc-bound mAb is recycled, whereas mAb-FcRn complexes linked via the Fab domain are either degraded or recycled directly to the first subcompartment. Such model scheme allows characterization of FcRn depletion in the presence of FcRn inhibitors.
. Anti-FcRn mAbs are allowed to bind to FcRn through either the Fab arms or Fc region. In the last subcompartment, Fc-bound mAb is recycled, whereas mAb-FcRn complexes linked via the Fab domain are either degraded or recycled directly to the first subcompartment. Such model scheme allows characterization of FcRn depletion in the presence of FcRn inhibitors.
There is also a growing interest in the role of hematopoietic cells in mAb PK (Challa et al., 2019; Malik and Edginton, 2020), as FcRn is expressed in these cells (Vidarsson et al., 2006; Latvala et al., 2017), and hematopoietic cells exist ubiquitously in the body (Yu et al., 2016). Experiments involving wild-type and hematopoietic cell-specific FcRn knockout mice have shown that endothelial and hematopoietic cells almost contributed equally to FcRn-mediated salvage (Akilesh et al., 2007; Montoyo et al., 2009; Richter et al., 2018). Correspondingly, the model mentioned above also considers mAb-FcRn interactions in endosomal space associated with hematopoietic cells, which are assumed to reside within the lymph, tissue interstitial space, and plasma (Li and Balthasar, 2019). However, widespread validation of such model remains unaccomplished.
Target-Mediated Drug Disposition
Target-mediated drug disposition (TMDD), a term coined by Levy (1994), refers to situations where high-affinity binding to the target impacts the PK characteristics of the drug. TMDD applies to the majority of TPs as this class of drugs is designed to have high affinity and specificity for their targets. However, its impact on the PK is only noticeable at lower TP concentrations when this pathway is not saturated. TMDD modeling has a history of about 20 years, and many seminal works have been done to establish the mechanistic framework, evaluate the identifiability of model parameters, simplify the model equations, and modify the model to characterize novel molecules. Interested readers are referred to (Mager and Krzyzanski, 2005; Gibiansky et al., 2008; Marathe et al., 2009; Gibiansky and Gibiansky, 2014; Lavezzi et al., 2018; Peletier and Gabrielsson, 2018) for detailed education on this topic. Only a few TMDD models will be highlighted below.
A full, generic TMDD model was proposed by Mager and Jusko (2001). The model assumes that drug in the central compartment (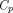 ) can distribute into the peripheral compartment (
) can distribute into the peripheral compartment (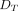 ), be cleared in its free form (via the elimination rate
), be cleared in its free form (via the elimination rate 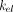 ), or bind (rate constant,
), or bind (rate constant, 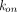 ) to the free target (
R) to form the drug-receptor complex (
) to the free target (
R) to form the drug-receptor complex (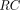 ).
R is produced (via the synthesis rate,
).
R is produced (via the synthesis rate, 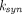 ) and eliminated (via the degradation rate,
) and eliminated (via the degradation rate, 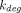 ) in the central compartment, whereas
) in the central compartment, whereas 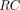 may undergo dissociation (
may undergo dissociation (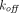 ) or internalization (
) or internalization (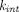 ). For soluble targets,
). For soluble targets, 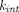 is usually close to
is usually close to 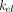 of the free drug. For membrane-bound targets,
of the free drug. For membrane-bound targets, 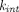 is often similar to
is often similar to 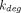 of the free receptor, and when this holds, the total receptor concentration (
of the free receptor, and when this holds, the total receptor concentration (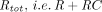 ) is constant, which eliminates the need to mathematically define temporal changes in
) is constant, which eliminates the need to mathematically define temporal changes in 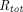 . Several approximations of the full TMDD model can be implemented to avoid estimating practically unidentifiable parameters such as
. Several approximations of the full TMDD model can be implemented to avoid estimating practically unidentifiable parameters such as 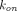 and
and 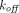 , and to make the equations less stiff. For example, when
, and to make the equations less stiff. For example, when 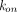 ,
, 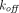 , and
, and 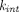 are much faster than the remaining processes, it can be assumed that the free drug, the free receptor, and complex are at quasi-steady-state, with
are much faster than the remaining processes, it can be assumed that the free drug, the free receptor, and complex are at quasi-steady-state, with 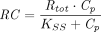 at all times, where
at all times, where 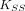 represents
represents 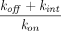 (Gibiansky et al., 2008). If
(Gibiansky et al., 2008). If 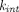 is much smaller than
is much smaller than 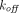 , the assumption of quasi-equilibrium becomes valid, where
, the assumption of quasi-equilibrium becomes valid, where 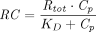 , with
, with 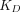 being
being 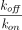 (Mager and Krzyzanski, 2005). Furthermore, if
(Mager and Krzyzanski, 2005). Furthermore, if 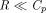 , both quasi-steady-state and quasi-equilibrium models can be reduced to Michaelis-Menten approximation (Gibiansky et al., 2008).
, both quasi-steady-state and quasi-equilibrium models can be reduced to Michaelis-Menten approximation (Gibiansky et al., 2008).
PBPK models usually adopt the full, quasi-steady-state, or quasi-equilibrium TMDD component in the tumor compartment (Urva et al., 2010; Shah and Betts, 2012; Cao and Jusko, 2014), using receptor and drug concentrations at the site of action instead of the central compartment (Fig. 1G). Parameters such as 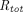 ,
, 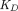 ,
, 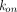 ,
, 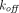 , or even
, or even 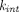 to operate these models could be obtained from in vitro measurements. Other physiologically relevant issues also need to be considered by these models, such as tumor antigen accessibility (discussed in Distribution Models) and antigen shedding. Many membrane-bound targets are known to shed the ectodomains or have a soluble form in the body (Kuang et al., 2010). This circulating pool competes with the cell-surface counterpart for drug binding and alters disposition and efficacy of the TP. A mPBPK-TMDD model incorporating the target-shedding mechanism of human epidermal growth factor receptor 2 (HER2) has systematically evaluated the effects of target shedding kinetics, soluble target turnover, and affinity difference between cell-surface HER2 and shed HER2, on plasma PK of trastuzumab (an anti-HER2 antibody), as well as receptor occupancy of membrane-bound HER2 (Li et al., 2014). Such TMDD model with target shedding was further modified and incorporated into a population PBPK framework to demonstrate the concentration of shed HER2 ectodomain as one of the key factors that contribute toward interindividual variability in trastuzumab PK (Malik et al., 2017).
to operate these models could be obtained from in vitro measurements. Other physiologically relevant issues also need to be considered by these models, such as tumor antigen accessibility (discussed in Distribution Models) and antigen shedding. Many membrane-bound targets are known to shed the ectodomains or have a soluble form in the body (Kuang et al., 2010). This circulating pool competes with the cell-surface counterpart for drug binding and alters disposition and efficacy of the TP. A mPBPK-TMDD model incorporating the target-shedding mechanism of human epidermal growth factor receptor 2 (HER2) has systematically evaluated the effects of target shedding kinetics, soluble target turnover, and affinity difference between cell-surface HER2 and shed HER2, on plasma PK of trastuzumab (an anti-HER2 antibody), as well as receptor occupancy of membrane-bound HER2 (Li et al., 2014). Such TMDD model with target shedding was further modified and incorporated into a population PBPK framework to demonstrate the concentration of shed HER2 ectodomain as one of the key factors that contribute toward interindividual variability in trastuzumab PK (Malik et al., 2017).
Renal Elimination
Kidney contributes to both catabolism and excretion of TPs. Renal excretion is a highly size-dependent process, and therefore is an important determinant of PK differences observed for TPs across a wide MW range. The molecular size cutoff for glomerular filtration is approximately 60 kD, and an inverse sigmoidal relationship between glomerular sieving coefficient (GSC) and MW has been demonstrated (Haraldsson et al., 2008). The size selectivity makes the renal filtration process fit well with the two-pore model, where GSCs can be expressed as empirical functions of MW (Li and Shah, 2019; Sepp et al., 2019). A pathway analysis reveals that lysosomal catabolism dominates the elimination of TPs with MW greater than 100 kD, and TPs less than 100 kDa are mostly eliminated via renal filtration (Li and Shah, 2019). In addition to size, other TP-specific factors also play a role in glomerular filtration. A positive correlation between GSC and molecular charge was also observed, which is attributed to the negatively charged glycocalyx of the filtration barrier (Haraldsson et al., 2008). A recent study reveals that renal filtration is higher for one-armed (nonbranched) IgGs and IgGs with a more flexible hinge region (Rafidi et al., 2021). More quantitative data on systemic and kidney PK of TPs are needed to incorporate factors such as charge, shape, and rigidity as covariates in PK models. Similar to other organs, renal endothelial cells can take up TPs for lysosomal degradation. Additionally, renal catabolism can occur via reabsorption into endocytic vesicles of proximal tubule cells following glomerular filtration or by peritubular extraction of TPs from postglomerular capillaries (Meibohm and Zhou, 2012), as shown in Fig. 1H. However, these catabolism mechanisms have not been explicitly accounted for in most current models.
Immunogenicity
TPs with antigenic components, such as foreign sequences and impurities, can induce immunogenicity and ADA formation. Although in rare cases ADAs serve as a storage depot that sustains TP exposures (Wang et al., 2008), they often compromise drug PK to varying degrees, depending on ADA titer, kinetics, and types (neutralizing or non-neutralizing).
Empirical models with time-varying PK parameters have been used to study the impact of immunogenicity on PK of TPs. For example, a parameter termed change in clearance time (
α) was included in a two-compartment TMDD model, which allows the linear clearance to suddenly change at time
α, presumably due to ADA formation (Kathman et al., 2016). It was found that the derived  can be much earlier than the time when ADA is detected in bioassays and thus is helpful in identifying false-negative subjects. Certain more mechanistic models introduce a compartment representing ADA depot that is activated by repeated dosing of TPs, and after some transit time, ADAs are available in the central compartment to bind to TPs and get eliminated (Chen et al., 2013; Perez Ruixo et al., 2013). The dissociation rate of ADAs binding to TPs can decay over time to reflect affinity maturation (Chen et al., 2013).
can be much earlier than the time when ADA is detected in bioassays and thus is helpful in identifying false-negative subjects. Certain more mechanistic models introduce a compartment representing ADA depot that is activated by repeated dosing of TPs, and after some transit time, ADAs are available in the central compartment to bind to TPs and get eliminated (Chen et al., 2013; Perez Ruixo et al., 2013). The dissociation rate of ADAs binding to TPs can decay over time to reflect affinity maturation (Chen et al., 2013).
These models are useful to determine the onset and magnitude of influence of ADA on TP disposition but cannot project immunogenicity based on in vitro and preclinical data. To aid the immunogenicity risk assessment during drug development, Chen et al. (2014a, 2014b) proposed a mechanistic, multiscale, prototype framework that integrates subcellular, cellular, and whole-body level models. The subcellular model focuses on antigen presentation processes, including activation of dendritic cells by endotoxin existent in TP formulations, internalization of the antigenic TP, degradation of the TP into T-cell epitope peptides, binding between peptides and major histocompatibility complex class II molecules, and presentation of T-epitope-MHC complexes on dendritic cell membrane. The cellular model further recapitulates activation, proliferation, and differentiation of T helper cells and B cells, which ultimately results in the secretion of ADAs from plasma cells. Total 17 subgroups of B cells and derived ADAs are assumed with incremental binding affinities to the antigenic TP so that the affinity maturation can be captured. The differential equation–based subcellular and cellular models are readily integrated with an extended two-compartment model to describe in vivo disposition of ADAs and the TP. Modeling the impact of immunogenicity on PK is achieved by adding the following two components to the clearance of TP: (1) rapid elimination of ADA-TP immune complex and (2) internalization of TP following B-cell receptor binding. Of note, such mechanistic modeling allows for incorporating drug-specific, product-specific, and patient-specific characteristics and can generate predictions of immunogenicity incidence and its influence on PK of TPs in a given population.
Models to Characterize TP Absorption
Due to the presence of proteolytic enzymes in the gastrointestinal tract, TPs are frequently administered via parenteral routes, such as intravenous, subcutaneous, and intramuscular delivery. subcutaneous administration has been approved for the delivery of many TPs as it is the most convenient route for chronic treatments and enables drug delivery for prolonged periods of time (McDonald et al., 2010). Subcutaneous dosing refers to injections into the hypodermis (interstitial space), from where TPs can gain access to the systemic circulation, via diffusion through blood capillaries (for TPs with MW <16 Kd) or convection through the lymphatic vessels (for TPs with MW >16 kD) that drain into the blood. For molecular modalities with Fc, FcRn-mediated transcytosis serves as an important pathway for the subcutaneous absorption (Deng et al., 2012; Richter and Jacobsen, 2014).
To model the absorption of TPs, an absorption site compartment can be linked to the central/plasma compartment via some absorption rate constants; the bioavailability can be explicitly expressed as F or reflected in a first-order degradation process from the subcutaneous site. Readers are referred to the review (Kagan, 2014) that describes applications of such empirical and semimechanistic models in characterizing subcutaneous absorption of diverse TPs, and physiologic interpretations of relevant parameters. In the PBPK framework, the subcutaneous site is often considered as a typical tissue compartment with vascular, endosomal, interstitial (i.e., the injection site), and cellular space. An extra clearance term is allowed either in the interstitial space or in the local lymphatic capillary to represent presystemic catabolism that occurs outside vascular endothelia, as shown in Fig. 1I (Porter and Charman, 2000).
Many physiologic factors such as FcRn expression, lymphatic vessel density and lymph flow rates, extracellular matrix, and injection sites, together with physicochemical properties of TPs such as MW, charge, aggregation potential, and immunogenicity, are known to influence PK following subcutaneous administration (Sanchez-Felix et al., 2020). Mechanistic models have been used to mathematically describe the interplay of these factors and to investigate their impacts on the extent and rate of subcutaneous absorption. Sensitivity analysis done in various models has revealed that 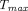 is most sensitive to lymphatic flow rate, whereas bioavailability is significantly impacted by lymphatic transit time, degradation during lymphatic transport, FcRn expression, and FcRn binding affinity (Zhao et al., 2013; Kagan, 2014). To mechanistically understand the effect of molecular size on subcutaneous absorption, a two-pore formalism can be applied in the subcutaneous site (Ibrahim et al., 2012; Gill et al., 2016; Hu and D'Argenio, 2020; Li et al., 2021), as discussed in Distribution Models. Pathway analysis using such two-pore models suggests that percentage of presystemic degradation increased with increasing MW of proteins, with the exception of mAbs due to FcRn-mediated protection, and that the fraction absorbed through lymphatic transportation becomes more prominent for larger-size TPs (Gill et al., 2016; Li et al., 2021). Positive charge patches on TPs are believed to interact with abundant hyaluronic acid, the highly negatively charged polysaccharides in subcutaneous space, which hinders the movement of molecules in the interstitium (Reddy et al., 2006; Mach et al., 2011). Correspondingly, proteins with higher pIs showed delayed
is most sensitive to lymphatic flow rate, whereas bioavailability is significantly impacted by lymphatic transit time, degradation during lymphatic transport, FcRn expression, and FcRn binding affinity (Zhao et al., 2013; Kagan, 2014). To mechanistically understand the effect of molecular size on subcutaneous absorption, a two-pore formalism can be applied in the subcutaneous site (Ibrahim et al., 2012; Gill et al., 2016; Hu and D'Argenio, 2020; Li et al., 2021), as discussed in Distribution Models. Pathway analysis using such two-pore models suggests that percentage of presystemic degradation increased with increasing MW of proteins, with the exception of mAbs due to FcRn-mediated protection, and that the fraction absorbed through lymphatic transportation becomes more prominent for larger-size TPs (Gill et al., 2016; Li et al., 2021). Positive charge patches on TPs are believed to interact with abundant hyaluronic acid, the highly negatively charged polysaccharides in subcutaneous space, which hinders the movement of molecules in the interstitium (Reddy et al., 2006; Mach et al., 2011). Correspondingly, proteins with higher pIs showed delayed 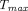 in lymph and reduced subcutaneous bioavailability (Reddy et al., 2006; Zheng et al., 2012). A two-pore PBPK model that intended to a priori predict human plasma PK of different-size TPs following subcutaneous failed to see any correlation between prediction accuracy of
in lymph and reduced subcutaneous bioavailability (Reddy et al., 2006; Zheng et al., 2012). A two-pore PBPK model that intended to a priori predict human plasma PK of different-size TPs following subcutaneous failed to see any correlation between prediction accuracy of 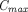 or
or 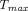 and TP pIs (Gill et al., 2016). In contrast, another two-pore PBPK model that allowed flexibility in subcutaneous lymphatic capillary clearance for 12 antibodies found a positive correlation between the parameter estimates and the positive charge in complementarity-determining regions (Hu and D'Argenio, 2020). Richer data from more TPs and a wider range of pI/charge are needed to validate and refine such correlations derived from the PBPK models.
and TP pIs (Gill et al., 2016). In contrast, another two-pore PBPK model that allowed flexibility in subcutaneous lymphatic capillary clearance for 12 antibodies found a positive correlation between the parameter estimates and the positive charge in complementarity-determining regions (Hu and D'Argenio, 2020). Richer data from more TPs and a wider range of pI/charge are needed to validate and refine such correlations derived from the PBPK models.
All the above-mentioned models can capture experimental data reasonably well, but their interspecies translatability and physiologic relevance remain questionable. It is well recognized that prediction of subcutaneous absorption in humans based on data from preclinical species is very difficult (Collins et al., 2020), which is largely attributed to interspecies differences in skin physiology (e.g., panniculus carnosus muscle is present in lower species but absent in humans) (Richter and Jacobsen, 2014), FcRn interactions (Ober et al., 2001), and relative contribution of lymphatics to the absorption (e.g., lymphatic absorption is important to subcutaneous bioavailability in sheep but less so in rodents) (Porter et al., 2001; Kagan et al., 2007). To our knowledge, traditional empirical models in conjugation with allometric scaling and mechanistic PBPK models do not seem to be capable of taking into account these complexities and robustly projecting bioavailability across species. In addition, it has been suggested that FcRn-mediated protection of mAbs in hematopoietic cells is important to subcutaneous bioavailability as the bioavailability was greatly compromised when FcRn was absent only in hematopoietic cells (Richter et al., 2018). The importance of this absorption mechanism needs to be thoroughly evaluated via modeling approaches.
Despite the predominant role of subcutaneous dosing in clinical TP therapies, other administration routes of TPs are gaining attention. Among them, noninvasive pulmonary delivery is experiencing renewed interest in view of the outbreak of COVID-19. Two marketed inhaled TPs, rhDNase I (Pulmozyme) and insulin (Afrezza), represent locally and systemically acting biologics via pulmonary entry, respectively. More than 25 inhaled TPs are being evaluated in clinical trials, targeting cystic fibrosis, asthma, and respiratory viral infections including COVID-19 (Liang et al., 2020). Pulmonary delivery takes advantage of the large surface area, extensive vasculature, relatively low proteolytic enzyme activity, and high permeability in the lung (Chung et al., 2012), with the potential to achieve rapid absorption for systemic delivery (Patton and Byron, 2007) and high local concentrations for topical therapy. Meanwhile, it faces challenges such as branching lung structures as barriers for deposition, limited fluid volume for particle dissolution (Patton et al., 2010), and rapid mucociliary and macrophage clearance. Therefore, mathematical lung submodels that incorporate salient anatomic features, spatial distribution of FcRn, fluid dynamics, protein transportation kinetics, and mucociliary clearance would be helpful in quantitative understanding of mechanisms underlying pulmonary absorption and guiding strategies to optimize TPs for inhalation. A multicompartment lung PBPK model originally intended for small molecules can serve as a starting template (Gaohua et al., 2015) and be further expanded to depict macromolecule-relevant processes.
Opportunities and Challenges
All the PK models for TPs described above have some advantages and disadvantages associated with them, which have been summarized in Table 1. Depending on their applicability, different models are frequently used in mechanistic preclinical studies and clinical settings to expedite drug discovery and development process (Glassman and Balthasar, 2019; Gibbs et al., 2020). The ultimate goal of investigating and modeling PK of TPs is to translate preclinical findings into humans and facilitate first-in-human dose selection and optimization of clinical dosing regimens. There is currently no consensus on the best way for interspecies scaling of TPs’ PK (Germovsek et al., 2021). Nonetheless, multiple attempts have been made to validate the capability of PK models to predict human PK from preclinical species or to extrapolate from human adults to pediatric populations, as listed in Table 2. Although detailed discussion of this topic is beyond the scope of this mini-review, cross-species and crosspopulation prediction of TPs’ PK is a promising and rapidly growing area. Going forward, more work needs to be done to reveal physiologic differences between species or populations that may impact ADME of TPs and to demonstrate general applicability of such PK models for a diverse array of TPs under different pathologic conditions. In this section, we have further discussed additional opportunities and challenges that PK scientists may face while developing mathematical models to characterize ADME of TPs.
Summary and characteristics of various PK models for TPs
Examples of models that have been validated for cross-species or crosspopulation predictability of TPs’ PK
Interantibody Differences in PK
The most prominent feature that distinguishes diverse TPs is the MW range (3.5 kDa to 150 kDa) and the size-dependent ADME mechanisms have been decently characterized using two-pore models. Nonetheless, mAbs with MW of around 150 kDa can still display very distinct PK profiles, even in cases where FcRn affinities are similar and TMDD is absent. Other key factors that are known to govern ADME properties of mAbs include charge, glycosylation, and shape, and some emerging models have attempted to address their influences on mAb PK.
Chen and Balthasar (2012) suggested two coefficients,  and
and  , that can be applied to modify the endosomal uptake clearance (
, that can be applied to modify the endosomal uptake clearance (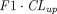 ) and transcapillary convection (
) and transcapillary convection (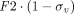 ), respectively, to account for interantibody variability in PK (Glassman et al., 2015). Using a similar yet augmented approach, Hu and D’Argenio (2020) applied four mAb-specific parameters in a PBPK model that represent antibody variabilities in the pinocytosis rate (
), respectively, to account for interantibody variability in PK (Glassman et al., 2015). Using a similar yet augmented approach, Hu and D’Argenio (2020) applied four mAb-specific parameters in a PBPK model that represent antibody variabilities in the pinocytosis rate (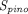 ), diffusive/convective transport rates (
), diffusive/convective transport rates (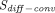 ), and lymphatic capillary uptake rate (
), and lymphatic capillary uptake rate (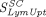 ) and presystemic clearance (
) and presystemic clearance (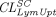 ) following subcutaneous dosing to individually fit intravenous and subcutaneous PK data of many mAbs in the training dataset. It was found that parameter estimates of both
) following subcutaneous dosing to individually fit intravenous and subcutaneous PK data of many mAbs in the training dataset. It was found that parameter estimates of both 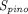 and
and 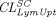 positively correlated with positive charges of the complementarity-determining region vicinity (PPC), consistent with the observations that increased positive charges of mAbs lead to enhanced cellular uptake and lower bioavailability (Bumbaca Yadav et al., 2015; Datta-Mannan et al., 2015). When these two relationships based on PPC were incorporated in the model, they were able to a priori predict subcutaneous PK of 3 out of 4 mAbs in the test dataset. Jones et al. (2019) also modeled the impact of molecular charge on mAb PK, using a somewhat different approach. Contrary to the predictor used in the model by Hu and D’Argenio (2020), PPC, which is theoretically calculated, this work used the data from affinity-capture self-interaction nanoparticle spectroscopy, an in vitro assay that detects nonspecific charge-based interactions as a covariate in the PBPK model. Instead of moderating the pinocytosis rate, the authors involved nonspecific binding between mAbs and cell membrane sites and internalization of the membrane-bound complex via pinocytosis. The nonspecific binding equilibrium constant was expressed as a function of scores from the in vitro assay, whereby greater self-association leading to higher binding affinity. After model calibration, mAb PK in mice and humans was predicted relatively well.
positively correlated with positive charges of the complementarity-determining region vicinity (PPC), consistent with the observations that increased positive charges of mAbs lead to enhanced cellular uptake and lower bioavailability (Bumbaca Yadav et al., 2015; Datta-Mannan et al., 2015). When these two relationships based on PPC were incorporated in the model, they were able to a priori predict subcutaneous PK of 3 out of 4 mAbs in the test dataset. Jones et al. (2019) also modeled the impact of molecular charge on mAb PK, using a somewhat different approach. Contrary to the predictor used in the model by Hu and D’Argenio (2020), PPC, which is theoretically calculated, this work used the data from affinity-capture self-interaction nanoparticle spectroscopy, an in vitro assay that detects nonspecific charge-based interactions as a covariate in the PBPK model. Instead of moderating the pinocytosis rate, the authors involved nonspecific binding between mAbs and cell membrane sites and internalization of the membrane-bound complex via pinocytosis. The nonspecific binding equilibrium constant was expressed as a function of scores from the in vitro assay, whereby greater self-association leading to higher binding affinity. After model calibration, mAb PK in mice and humans was predicted relatively well.
Modeling approaches incorporating the impact of glycosylation on mAb PK are less explored. This is in part due to inconsistent observations of the effect of high mannose (Kanda et al., 2007; Yu et al., 2012), hybrid type glycans (Kanda et al., 2007; Falck et al., 2021), and galactosylation (Wright et al., 2000; Falck et al., 2021) on clearance. As glycoengineering of TPs gain more popularity, it can be expected that glycosylation will be an important covariate in PK models. As has been discussed in Renal Elimination, more data are needed to substantiate the relationship between molecular shape, charge, or rigidity and kidney elimination. Ultimately, a platform PBPK model incorporating physicochemical characteristics of TPs holds promise for predicting PK based on in silico and in vitro properties and guiding protein engineering strategies to achieve maximum and specific exposure at the site of action.
Modeling Next-Generation TPs
Innovative protein engineering technologies have paved the way for the generation of an array of novel TPs, which often possess unique physicochemical properties and mechanisms of action. Mechanistic models need to be evolved to understand determinants controlling their PK/PD and to aid in rational design of these next-generation modalities. Previous models may work well in capturing existent data, but novel molecules and unusual scenarios often require reexamination of model assumptions and refinement of model structures. Based on the types of modeling efforts required to elucidate the ADME mechanisms, these next-generation TPs can be roughly categorized into two nonexclusive groups.
The first group of TPs necessitate highly mechanistic cellular models to characterize intracellular processing, due to endosomal-environment switch mechanisms, or their intracellular-delivery nature. The well-known concept of “recycling antibodies” has been applied to IL-6R, IL-6, and PCSK 9, where antibodies bind tightly to the target extracellularly at pH 7.4 or with low calcium ion concentration and dissociate rapidly from the target in endosomes where pH is low or calcium ion is concentrated. These “catch-and-release” mAbs are expected to improve neutralization of soluble targets, and detailed modeling work has identified target turnover and pH-dependent binding affinity difference that maximize target clearance (Glassman and Balthasar, 2016a; Yang et al., 2017; Jones et al., 2020). The acid-switched binding is also of interest for membrane-bound targets (Kang et al., 2019), but relevant modeling analysis is scarce. ADCs are a class of drugs for which complex ADME properties have been extensively evaluated in PKPD models. Multiscale models have been developed to characterize systemic disposition and intracellular processing of the intact ADC, the antibody moiety, and the free drug (Maass et al., 2016; Khot et al., 2017; Singh and Shah, 2017a; Singh and Shah, 2017b; Singh et al., 2020). In recent years, biparatopic ADCs that recognize two nonoverlapping epitopes of the same target have gained much interest. Such constructs are believed to promote receptor clustering, inhibit receptor recycling, and promote lysosomal trafficking of the receptor and ADCs, thereby increasing cytotoxic drug release, as exemplified by biparatopic ADCs targeting HER2 (Li et al., 2016), MET (DaSilva et al., 2021), and EGFR (Fan et al., 2021). A mechanistic model can provide a quantitative understanding of the extent to which intracellular trafficking is altered, the resultant drug exposure improvement, and the long-term impact of receptor downregulation caused by clustering.
The second type of next-generation TPs use previously less-understood receptor-mediated disposition pathways. For example, exploiting transferrin receptor (TfR)-mediated transcytosis has been recognized as a strategy to enhance drug delivery across the BBB, as demonstrated using ADCs or bispecific mAbs targeting both TfR and therapeutic targets (Friden et al., 1991). Intriguingly, higher antibody exposure in the brain is observed when TfR engagement is monovalent or has only intermediate affinity (Yu et al., 2011; Niewoehner et al., 2014; Chang et al., 2021b), which ensures both sufficient TfR binding at the luminal side and efficient release to the abluminal side. Empirical and semimechanistic PKPD models have been explored to predict the optimal TfR affinity that maximizes brain exposure, as well as the impact on efficacy and safety (Gadkar et al., 2016; Kanodia et al., 2016). However, the influence of TfR binding valency has not been characterized, and translation of mouse and monkey models to human remains to be validated. Fc gamma receptor (FcγR)-mediated elimination represents another pathway that can play a role in TP disposition. FcγRs are known to be important in immune responses to mAbs, but their role in mAb PK is less defined. Although experiments with FcγR knockout mice suggested a minor role of FcγR in PK of a typical IgG1 molecule (Abuqayyas and Balthasar, 2012), for those TPs that can form large, high-order immune complexes with soluble ligands (Mortensen et al., 2012; Kasturirangan et al., 2017), or that have significant ADCC resulting in target cell depletion (Uchida et al., 2004), interaction with FcγRs may impact TP disposition. However, a systematic modeling analysis of this pathway is currently lacking. Another modality that falls in this category is albumin-fusion or albumin binding domain (ABD)-conjugated TPs, which leverages pH-dependent albumin-FcRn interactions to achieve half-life extension. This strategy has been applied to IgA (Meyer et al., 2016), single-chain diabodies (Stork et al., 2007), single-chain variable fragments (Sanches et al., 2020), domain antibodies (Goodall et al., 2015), and affibodies (Andersen et al., 2011). A PBPK framework with the two-pore formalism has been demonstrated to well characterize PK of albumin, ABDs, and ABD-conjugated diabody (Sepp et al., 2019; Sepp et al., 2020). However, a more extensive evaluation of how the size of the unmodified TP and the size of the albumin-binding modality/albumin variants impact the half-life of TPs is still needed.
Conclusions
Mathematical and mechanistic PK models are crucial for the development of exposure-efficacy and exposure-toxicity relationships for TPs in preclinical species and humans. Here, we underscore the potential of PBPK modeling in characterizing unique ADME properties of TPs and demonstrate a diverse array of models with variable assumptions in describing transcapillary transport, tissue distribution, FcRn-mediated recycling, TMDD, renal elimination, and absorption. These models shed light on critical determinants influencing TPs’ exposures in circulation or at the site of action and target engagement. We also highlight the emerging needs to integrate physicochemical properties of TPs in PK models to explain intermolecular PK variability and to elucidate novel disposition mechanisms of next-generation TPs using novel models. It is anticipated that the advanced PK models will facilitate triaging of TP candidates and optimization of molecular design. These quantitative tools can also facilitate model-informed discovery and development of biotherapeutics.
Authorship Contributions
Wrote or contributed to the writing of the manuscript: Liu, Shah.
Footnotes
- Received March 9, 2021.
- Accepted January 31, 2022.
D.K.S. is supported by National Institutes of Health National Institute of General Medical Sciences [Grant GM114179], the Center of Protein Therapeutics at the University at Buffalo, National Institute of Allergy and Infectious Diseases [Grant AI138195], and National Cancer Institute [Grant R01-CA246785] and [Grant R01-CA256928] (to D.K.S.).
No author has an actual or perceived conflict of interest with the contents of this article.
Abbreviations
- ABD
- albumin binding domain
- ADA
- antidrug antibody
- ADC
- antibody-drug conjugate
- ADME
- absorption, distribution, metabolism, and elimination
- BBB
- blood-brain barrier
- BCSFB
- blood-cerebrospinal fluid barrier
- CSF
- cerebrospinal fluid
- Fab
- antigen binding fragment
- Fc
- fragment crystallizable
- FcγR
- Fc gamma receptor
- FcRn
- neonatal Fc receptor
- GSC
- glomerular sieving coefficient
- mAb
- monoclonal antibody
- mPBPK
- minimal physiologically based pharmacokinetics
- MW
- molecular weight
- PBPK
- physiologically-based pharmacokinetics
- PD
- pharmacodynamic
- PK
- pharmacokinetic
- PPC
- the patches of positive charge
- TMDD
- target-mediated drug disposition
- TfR
- transferrin receptor
- TP
- therapeutic protein
- Copyright © 2022 by The American Society for Pharmacology and Experimental Therapeutics