Advertisement
Research ArticleArticle

Pharmacokinetic Consequences of Induction of CYP2E1 by Ligand Stabilization

Jenny Y. Chien, Kenneth E. Thummel and John T. Slattery
Drug Metabolism and Disposition October 1997, 25 (10) 1165-1175;

Abstract

Models of the time course of the effect of P450 induction on substrate clearance have previously only considered induction through enhanced synthesis of protein. Induction of CYP2E1 does not always conform to this model, in that many chemicals induce the enzyme through stabilization of the protein apparently by binding to the active site. While such binding protects the enzyme from degradation, it also results in competitive inhibition of substrate clearance. We present a model based on experimental studies of chemical induction of CYP2E1 by ligand stabilization through which this mechanism of induction can be translated into its pharmacokinetic consequence with regard to clearance of substrate. CYP2E1 is considered to be localized in two pools: Pool 1 at which two mechanisms of degradation, fast and slow, operate and pool 2, at which only the slower mechanism operates. Binding of substrate to enzyme in pool 1 stabilizes it from degradation by the fast process, leaving only the slow process. Ligand stabilization therefore results in induction of CYP2E1 as enzyme accumulates as a consequence of unchanged synthesis. Binding of ligand to the active site results in competitive inhibition of the clearance of substrate. Model-based computer simulations show that the time course of interaction between inhibitor/inducer and substrate can be predicted from knowledge of I/Ki and S/Km and the synthesis and degradation kinetics of CYP2E1. The simulations demonstrate further that as long as inhibitor/inducer administration is not interrupted, the clearance of substrate will always be less than the value observed at low concentration of substrate even if the substrate concentration is raised to displace inhibitor/inducer from the active site. On the other hand, the degree of inhibition of clearance is less than would be seen if induction had not taken place. Clearance of substrate is observed to rise above the value observed in the absence of the inhibitor/inducer only after the inhibitor/inducer concentration declines low enough for substrate to gain access to the active site of the enzyme. The model-based simulations agree with reports of the interaction between isoniazid and acetaminophen in humans.

Cytochrome P450 2E1 (CYP2E1)1 is a constitutive and inducible mammalian form of the super family of cytochrome P450 enzymes (1-2). Physiologic and pathologic conditions associated with the induction of CYP2E1 include birth (3-5), fasting (6), obesity (7-8), and diabetes (9-11). These conditions modulate the level of mRNA via transcriptional activation, post-transcriptional activation, message stabilization, or some combination of these mechanisms (12-16). The biologic consequence of each of these mechanisms of induction is an increase in thede novo synthesis of CYP2E1 protein.

The pharmacokinetic consequences of induction via increasedde novo synthesis are well understood, as classical inducers such as 3-methylcholanthrene and phenobarbital fit into this group (17-20). This general mechanism results in a first-order rise in functional enzyme and substrate clearance to a new stable plateau that is maintained as long as the administration of the inducer is not altered (21-23).

Induction by Stabilization.

Chemical inducers of CYP2E1 in animals include isoniazid, imidazoles, pyridine, and other small molecular weight alcohols, as well as substances produced endogenously such as acetone (1-2, 15, 24-25). Chemical induction of CYP2E1 occurs either by increasing de novo synthesis or by decreasing degradation of the protein. Stabilization of CYP2E1 protein is of particular interest because the consequences of this mechanism with regard to the metabolism of substrates in vivo have only recently been systematically probed (26-30). The phenomenon of CYP2E1 stabilization was first shown with acetone in rats (14). In vivo labeling of protein and subsequent immunopurification demonstrated that native CYP2E1 protein turnover followed a biphasic pattern with respective half-lives of 7 and 37 hr. Treatment with acetone abolished the rapid component such that only the longer half-life was observed. Separate labeling data suggested that there was an apparent decrease in the de novosynthesis rate of CYP2E1 with acetone administration. This result indicated that induction of CYP2E1 by acetone is primarily due to stabilization of CYP2E1.

CYP2E1 induction through stabilization by ethanol has been demonstrated in rats at peak plasma ethanol concentrations ranging from 1.0 to 2.5 mg/ml (5, 31-34). In this concentration range, CYP2E1 activity and immunodetectable CYP2E1 in liver microsomes from ethanol-induced rats was increased in the absence of an increase in specific mRNA. In agreement with the results of CYP2E1 induction by acetone, CYP2E1 protein turnover followed a biphasic pattern, and ethanol treatment abolished the rapid CYP2E1 turnover phase (34-35).

Stabilization of CYP2E1 has also been demonstrated in primary cultures of rat hepatocytes with several small molecular weight ligands. A correlation between the binding affinities of ligands to the active site of CYP2E1 and their ability to prevent the loss of the enzyme has been demonstrated (36). CYP2E1 protein was maintained by ligand even when mRNA rapidly disappeared, showing that the maintenance of CYP2E1 in primary hepatocyte culture was independent of enzyme synthesis.

Taken together, the results of these studies indicate that binding of a ligand to the active site of CYP2E1 protects the protein from degradation, allowing it to accumulate as a consequence of unaltered synthesis.

Pharmacokinetic Consequence in Animals.

The consequence of induction by ligand stabilization with regard to drug metabolism was first illustrated in a study of the effect of chronic ethanol administration on the defluorination of enflurane (37), a substrate of CYP2E1 (38-39). In vivo ethanol administration increased defluorination ex vivo in microsomes prepared from rats in which the plasma concentration of ethanol was ≥ 0.6 mg/ml, as expected after induction of CYP2E1. However, at the same ethanol concentration, in vivodefluorination was inhibited. The in vivo enflurane defluorination increased above the pre-ethanol rate only when plasma ethanol concentration decreased to ≤ 0.5 mg/ml. These results are consistent with the ligand-stabilized mechanism of induction in that inhibition was observed in vivo at high concentrations of ethanol. Enhanced activity was observed in microsomes prepared at the same time since ethanol would be removed during preparation of the microsomes. In vivo defluorination of enflurane was enhanced (revealing the consequence of induction) as ethanol was eliminated and CYP2E1 became available for binding of substrate.

Similar results have been demonstrated with another CYP2E1 substrate, ethyl carbamate, in rats and mice induced with pyridine (40). CYP2E1 catalyzes the bioactivation of ethyl carbamate to a reactive epoxide and administration of pyridine inhibited the metabolism of [14C]-ethyl carbamate to its [14C]-epoxide in vivo. However, formation of this metabolite was enhanced in microsomes prepared at the same time after pyridine administration.

Pharmacokinetic Consequence in Humans.

The pharmacokinetic consequences of CYP2E1 induction have been studied in humans using isoniazid as the inducer and formation of the hepatotoxin N-acetyl-p-benzoquinone imine (NAPQI) from acetaminophen (41, 42) or chlorzoxazone 6-hydroxylation as a probe of CYP2E1 activity (43). That isoniazid stabilizes CYP2E1 has been suggested by an increase in CYP2E1 protein in microsomes of isoniazid-treated animals in which there was no increase in specific mRNA (16, 33).

In the first two of a series of studies (26-30), acetaminophen pharmacokinetics were determined on three occasions in healthy subjects administered isoniazid daily for several days: before isoniazid administration was initiated, together with isoniazid, and 48 hr after the last dose of isoniazid. When acetaminophen was ingested together with isoniazid, a 66% inhibition was observed in the oxidative metabolism of acetaminophen to NAPQI. At 48 hr after the withdrawal of isoniazid, NAPQI formation had returned to the pre-isoniazid value (26). In the second study (27), NAPQI formation was inhibited by 66% when acetaminophen was taken together with isoniazid. At 24 hr after the last dose of isoniazid, a 56% increase in the formation of NAPQI was observed, but it had returned to the pre-induced level 72 hr after the discontinuation of isoniazid. In this study the effect of isoniazid on chlorzoxazone clearance was also examined. When chlorzoxazone was taken together with isoniazid, chlorzoxazone clearance was inhibited by 58% in comparison to the pre-isoniazid control. At 48 hr after the last dose of isoniazid, there was a 50% increase in chlorzoxazone clearance, but this had returned to the pre-isoniazid level 96 hr after the last isoniazid dose.

The influence of isoniazid acetylation status on the interaction between isoniazid and acetaminophen in patients receiving a morning dose of isoniazid for a period of at least 6 months for prophylaxis of tuberculosis was consistent with expectations based on induction of CYP2E1 by stabilization (28). Acetaminophen was administered on separate occasions, either with the morning dose of isoniazid or in the evening 12 hr after the morning dose of isoniazid. At the conclusion of isoniazid therapy, a time-matched control phase (morningversus evening) of acetaminophen administration was performed. When acetaminophen and isoniazid were co-administered, the mean NAPQI formation clearance was inhibited by 64% in slow acetylators and by 52% in fast acetylators. When acetaminophen was given 12 hr after isoniazid, the mean NAPQI formation clearance in fast acetylators was increased 37% from the value observed in the absence of isoniazid therapy, but remained inhibited by 32% in slow acetylators, as expected if isoniazid was still present in those individuals in whom it would be eliminated more slowly.

A similar study was conducted in which chlorzoxazone was used as a probe of CYP2E1 activity (30). Co-administration of chlorzoxazone with isoniazid resulted in 80% inhibition of chlorzoxazone clearance in slow acetylators and 60% in fast acetylators. At 48 hr after the last dose of isoniazid, 6-hydroxy chlorzoxazone formation in slow acetylators was still increased by 60% and had returned to the pre-isoniazid value in fast acetylators.

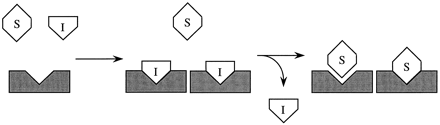
Isoniazid inhibition and enhancement of NAPQI formation and chlorzoxazone clearance in humans are consistent with induction of CYP2E1 via ligand-stabilization, a mechanism likely to result in persistent inhibition of activity while the inhibitor/inducer is present and enhancement of activity after the inducer is eliminated. The time of reversal from inhibition to enhanced activity depends on the ability of the substrate to compete for the active site as the inhibitor/inducer ligand is eliminated. This mechanism is illustrated in fig. 1.

Figure 1
Figure 1

Stabilization of CYP2E1 by active site occupation.

Inhibitor/inducer and substrate are I and S, respectively, and CYP2E1 is represented by the shaded block. Competitive inhibition of CYP2E1 occurs as the inhibitor/inducer binds to the active site, blocking substrate access. As a consequence of binding, CYP2E1 accumulates due to stabilization. As the inhibitor/inducer is removed, substrate regains access to the active site, and the metabolism of substrate is enhanced.

We have developed a pharmacokinetic model to describe the extent and consequences of enzyme inhibition/induction by ligand-stabilizationin vivo as a function of the affinities and concentrations of the inhibiting/inducing ligand and the substrate for the active site. Simulations conducted based on this model are consistent with the time course of interactions observed in humans and animals.

Theoretical

Model Characteristics.

There are conflicting putative mechanisms by which CYP2E1 is degraded. An ATP/ubiquitin-mediated proteolytic degradation in animals has been demonstrated by two groups of investigators (34, 44). Others suggest that the rapid phase of degradation is accounted for by a Mg/ATP-dependent phosphorylation, while an autophagosomal/autolysosomal process accounts for the slower phase (45-47). Although the biochemical mechanism(s) by which CYP2E1 is degraded are controversial, there is consensus from pulse labeling and immunopurification studies on the biphasic nature of its degradation (14, 34-35).

Several possible models that might result in biphasic loss of CYP2E1 can be proposed. The simplest model consists of a single pool of enzyme in which an endogenous ligand is assumed to slow the otherwise rapid degradation of CYP2E1. However, unless the ligand has a very slow dissociation constant (such that the half-life of dissociation would be several hours), thus making dissociation of the ligand the rate limiting step in the degradation of protein, the kinetics of CYP2E1 in this model are monophasic with a half-life that is a function of the dissociation constant and the elimination rate constants. Accordingly, an appropriate model must consider two kinetically separate pools of enzyme.

Kinetically distinct pools are most easily envisioned as chemically or physically distinct. Chemically distinct forms of the enzyme might be produced by post-translational modifications that do not compromise activity. While such a model would result in appropriate CYP2E1 degradation kinetics, there is no evidence for a post-translational modification of CYP2E1 that maintains catalytic activity. Physically distinct pools of catalytically competent CYP2E1 may exist. Catalytically competent CYP2E1 is present in the endoplasmic reticulum and the Golgi apparatus although the Golgi compartment accounts for relatively little enzyme (48). It is most likely that CYP2E1 in the Golgi arises from the smooth endoplasmic reticulum, while new CYP2E1 appears first in the rough endoplasmic reticulum. It is conceivable that the fast process of degradation operates at only one of these sites, while both processes can operate at the other. Thus, it is reasonable to consider a model in which the enzyme in the rapidly turned-over pool can be stabilized by ligand and thereby be protected from degradation by the fast process while it is still degraded by the slow process.

Several classes of model with physically distinct pools of catalytically competent enzyme can be envisioned. The first allows insertion of new enzyme into both pools without any transfer of enzyme between the pools. One pool has a rapid rate of degradation, which is slowed when ligand binds, while the other has only a slow rate. A second class that produces biphasic kinetics of CYP2E1 loss with physically distinct pools is characterized by insertion of newly synthesized protein into either the rapidly turned over pool or both of the pools and translocation of the protein in either or both directions between the compartments. If there is no translocation from the rapid to the slow pool, stabilization of the protein in the rapidly degraded pool will result in induction of the protein only within that pool. If translocation occurs from the rapidly turned over pool to the more slowly turned over pool, induction by stabilization in the rapidly turned over pool will generally result in an increase of enzyme in the more slowly turned over pool as well. Otherwise, the kinetic characteristics of these models are similar.

It is not clear which model is biochemically correct. However, initial simulations showed that to obtain induction to the extent observed in experimental animals, translocation from the rapidly turned over pool to the slowly turned over pool was required. Also, synthesis into one pool (viz. the rough endoplasmic reticulum pool) seemed most appropriate. Since the kinetic characteristics of the two pool class of models are similar, we present equations describing a model in which new enzyme is added to pool 1 only (viz. rough endoposamic reticulum). Enzyme in pool 1 is subject to a rapid degradation process when unbound by ligand and a slow degradation process when bound. The model is illustrated in fig. 2. Either free or bound enzyme can be translocated to pool 2, viz. smooth endoplasmic reticulum, as a consequence of either loss of ribosomes or by contact between the rough and smooth endoplasmic reticulum (48-52). Enzyme in pool 2 is degraded only by the slow process.

Figure 2
Figure 2

Proposed two-compartment model consisting of two physically distinct pools of CYP2E1.

Rsyn is the rate of synthesis, a constant zero-order input into pool 1. The rapid degradation rate constant of the unbound enzyme in pool 1 (E1,free) is kdeg,fast. The degradation rate constant of the stabilized enzyme E1,boundand the bound and unbound enzyme in pool 2 (E2,bound and E2,free) is kdeg,slow. The transfer rate constant of enzyme from pool 1 to pool 2 is ktrans.    

Mathematical model.

The rate of change in tissue content of total CYP2E1 prior to induction by ligand stabilization is described as the sum of two rate equations describing the respective pools of enzyme:dE1dt=Rsyn−Rdeg,1−Rtrans dE2dt=Rtrans−Rdeg,2 Rsyn is the constant zero-order rate of protein synthesis, which is not altered by the inducer. Rdeg,1 and Rdeg,2 are the rates of degradation in the respective pools and Rtrans describes the rate of transfer of enzyme from E1 to E2.

The rates can be written as the product of the respective rate constant and the concentration of the appropriate pool of the enzyme.dE1dt=Rsyn−E1·kdeg,fast−E1·ktrans dE2dt=E1·ktrans−E2·kdeg,slow where kdeg,fast is the first-order degradation rate constant of the rapidly turned-over unbound enzyme in pool 1, kdeg,slow is the rate constant for the turnover of enzyme in pool 2 (and bound enzyme in pool 1) and ktrans is the rate constant of transfer of enzyme from pool 1 to pool 2.

Upon induction with acetone or ethanol in vivo, the ligand-stabilized CYP2E1 is turned over at the same rate as the slowly turned over pool (pool 2) of enzyme. In contrast, the binding of the ligand to CYP2E1 in the slow pool does not alter the kinetics of degradation in this pool, although it can bind to CYP2E1 in pool 2. The rate equations describing the model when inhibiting/inducing ligand is introduced are:dE1dt=Rsyn−E1·fu(kdeg,fast+ktrans)−E1·fb(kdeg,slow+ktrans) dE2dt=E1·ktrans−E2·kdeg,slow where fu and fb, respectively, represent the fractions of free and ligand-bound enzyme. Both bound and free enzyme in pool 1 can be transferred to pool 2. The amount of enzyme in pool 2 is dependent on the rate of transfer from pool 1.

The bound and free enzyme fractions are functions of the inducer concentration, I, and the equilibrium dissociation constant, Ki, of the (competitive2) inhibitor/inducer.fb=I/Ki1+I/Ki fu=11+I/Ki E0 is the constitutive level of enzyme in the pre-induced steady-state, where dE1/dt = 0. Under this condition,Rsyn=E0,1(kdeg,fast+ktrans) Substituting the expressions for binding and Rsyn into enzyme rate equations yields a set of equations expressing the change in enzyme level as a function of the inhibitor/inducer concentration, the binding affinity, and the rate constants:dE1dt=E0,1(kdeg,fast+ktrans)−E1·I/Ki1+I/Ki (kdeg,slow+ktrans)−E11+I/Ki (kdeg,fast+ktrans) Equation 1dE2dt=E1·ktrans−E2·kdeg,slow Equation 2

Clearance.

The basal clearance of a specific substrate in the absence of the inducer, Cl0, is described by the single-enzyme Michaelis-Menten equation:Cl0=E0·kcatKm+S Equation 3Clearance at time “t” in the presence of the competitive inducer/inhibitor is therefore described byCl(t)=E·kcatKm(1+I/Ki)+S Equation 4The ratio of clearance described in eq. 4 to basal clearance described by eq. 3 is a function of S/Km and I/Ki, and the ratio of induced enzyme to basal enzyme concentration,Cl(t)Cl0=E(1+S/Km)E0(1+I/Ki+S/Km) Equation 5The clearance ratio in this case (referred to as “case 1” below) in the pre-induced state will always be 1 at any value of substrate concentration. The ratio is therefore a measure of clearance at a given concentration of substrate in the presence of the inhibitor/inducer to the value in the absence of the inhibitor/inducer but at the same concentration of substrate.

An alternative case (“case 2”) can be constructed in which the basal clearance (Cl0) is the clearance in the absence of the inhibitor/inducer and when S ≪Km. In this case, Cl(t) is compared with clearance observed in the absence of inhibitor/inducer andat vanishingly low substrate concentration, regardless of the concentration of substrate influencing the value of Cl(t). Thus, the basal clearance, Cl0,(S/Km→0), is defined as E0·kcat/Km. The ratio of Cl(t) described in eq. 4 to this basal clearance thus becomes:Cl(t)Cl0,S/Km→0=EE0(1+I/Ki+S/Km) Equation 6As eq. 6 indicates, the expression of clearance relative to the basal clearance at vanishingly low substrate concentration does not restrict the consideration of larger values of S/Km as a determinant of the value of Cl(t). Thus, S/Km remains in the sum in the denominator.

Enzyme at Steady-State.

As the enzyme concentration reaches steady-state at a steady-state inhibitor/inducer ligand concentration, dEss,total/dt = 0. The total amount of enzyme is the sum of eqs. 1 and 2 under the condition of steady-state:Ess,total=E0,1(kdeg,fast+ktrans)(1+I/Ki)(1+ktrans/kdeg,slow)kdeg,fast+ktrans+I/Ki(kdeg,slow+ktrans) The ratio of the amount of enzyme at steady-state in the presence of the inhibitor/inducer to the amount in its absence, Ess/E0, is obtained by dividing by the equalityE0,total=E0,1(1+ktrans/kdeg,slow) thus,Ess,totalE0,total=(kdeg,fast+ktrans)(1+I/Ki)kdeg,fast+ktrans+I/Ki(kdeg,slow+ktrans) Equation 7

Clearance at Steady-State.

An expression for clearance at steady-state and amount of enzyme is obtained by substituting eq. 7 into eq. 5 where the pre-induced basal clearance is Cl0 = E0·kcat/(Km+S).Embedded Image Equation 8On the other hand, substituting eq. 7 into eq. 6, where the basal clearance is Cl0,(S/Km)→0 = E0·kcat/Km, yields an equation that describes the change in clearance relative to clearance at low substrate concentration:ClssCl0,S/Km→0=(kdeg,fast+ktrans)(1+I/Ki)(kdeg,fast+ktrans+I/Ki(kdeg,slow+ktrans))(1+I/Ki+S/Km) Equation 9The degree of inhibition of clearance can be examined apart from the degree of induction by dividing Cl by E (Cl/E) as described by eqs. 7 and 8, where the basal clearance is E0·kcat/(Km+S).Clss·E0Cl0·Ess=1+S/Km1+I/Ki+S/Km Equation 10At Cl0,(S/Km)→0 = E0·kcat/Km, the inhibited clearance (Cl/E) can be expressed as described by eqs. 7 and 9.Clss·E0Cl0,S/Km→0·Ess=11+I/Ki+S/Km Equation 11

Computer Simulations

Model Implementation.

In the time course simulations that follow, the inhibitor/inducer ligand concentration was simulated as a constant-rate infusion, followed by a first-order rate of elimination after the infusion was discontinued:I(t)=Iss(1−e−kt)−§(t)Iss(1−ek(T−t)) where §(t) is a step function with a value of 0 for ± ≤ T and 1 for ± > T. T is time of infusion. In the time course simulations, inhibitor/inducer was infused at a constant rate for 350 hr. A Ki value of 40 μM and a half-life of 3 hr were used as these values are consistent with isoniazid data in humans. Clearance at any time during and after infusion of inhibitor/inducer was calculated as if the substrate were instantaneously introduced. Thus, the enzyme was modeled as being increased by inhibitor/inducer, not by continuous exposure to substrate.

The initial division of CYP2E1 between the pools was estimated by simulating the time course of total enzyme with varying fractions in the pools. Since approximately 50% of the total area under the curve in the rat is described by pool 1 (14, 34), the appropriate basal division of total enzyme between the pools was the fraction that satisfied this condition: 85% in pool 1 and 15% pool 2. The degradation rate constants correspond to half-lives of 7 and 37 hr in the rat. ktrans was calculated from the steady-state pre-inhibitor/inducer condition for pool 2, ktrans = kslow·E0,2/E0,1, and corresponded to a half-life of 196 hr.

Eqs. 1, 2, 5, and 6 were used to simulate time course of enzyme level and substrate clearance. Eq. 7 was used to simulate steady-state enzyme level as a function of I/Ki and S/Km. Eqs. 8 through 11 were used to simulate the steady-state conditions of inhibitor/inducer, enzyme level, substrate clearance and inhibited clearance (Cl/E) as functions of I/Ki and S/Km. Simulations were performed using Mathmatica version 2.1.0.2 (Wolfram Research, Inc. Champaign, IL) implemented on a Macintosh computer.

Model Validation

The model was assessed by evaluating key expected results in simulations of (1) enzyme turnover after administration of a radio-labeled precursor amino acid, (2) the effect of ligand stabilization on the time course of total enzyme and the amount of total enzyme at steady-state, and (3) the effect of competitive inhibition alone on clearance of substrate, examined by dividing the clearance by enzyme amount.

Enzyme Turnover in the Two Pools.

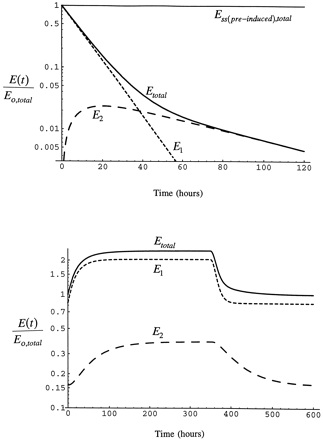
Fig. 3 shows a simulation of the elimination of a pulse dose of radiolabeled enzyme formed by the administration of a radiolabeled precursor. This is accomplished by setting the rate of synthesis of enzyme to zero after enzyme is at steady-state. The simulation shows the characteristics required of the decline of enzyme. Decline of total enzyme is biphasic with half-lives of 7 and 37 hr, corresponding to the respective half-lives for pools 1 and 2 in the rat. Since newly synthesized enzyme appears first in pool 1, the amount of labeled enzyme in pool 2 rises to a maximum as it is transferred from pool 1 to pool 2. Also shown in fig. 3 is the time course of enzyme accumulation in the respective pools and the return to the pre-inhibitor/inducer condition after the end of the infusion. True steady-state is reached in the system by 200 hr after the beginning of the infusion and the pre-inhibitor/inducer condition is re-attained by 200 hr after the end of the infusion, times consistent with the longer of the CYP2E1 half-lives. However, steady-state and return to baseline is approximated much earlier in pool 1 and total CYP2E1 since the short half-life contributes to enzyme elimination unless the enzyme is completely bound.

Figure 3
Figure 3

Time course of CYP2E1.

Time course of loss of CYP2E1 after a pulse label of precursor simulated with eqs. 1 and 2 in the absence of inhibitor/inducer (upper panel). Ess(pre-induced)total is total CYP2E1 in the absence of inhibitor/inducer at steady-state. The lower panel shows the time course of the accumulation of enzyme in the respective pools during infusion of inhibitor/inducer for I/Ki = 2 and the return to the pre-induction level after the end of the infusion.

Effect of Inhibitor/Inducer on Enzyme Amount.

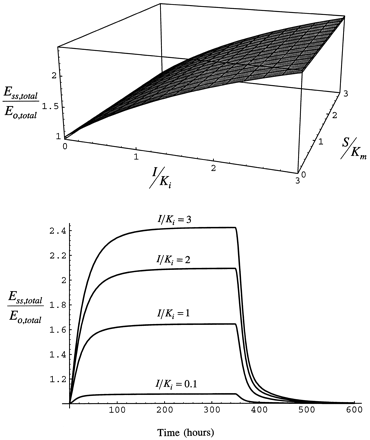
Fig. 4 shows that infusion of inhibitor/inducer to steady-state (achieved at 24 hr after the start of the infusion) causes a rise in enzyme that is a function of I/Ki and not S/Km, as the model was constructed to allow evaluation of the effect of the inhibitor/inducer alone on enzyme behavior rather than to allow the contributions of inhibitor/inducer and substrate to interact.

Figure 4
Figure 4

Upper panel: Steady-state level of total enzyme as a function of I/Ki and S/Km while the infusion of the inhibitor/inducer continues (eq. 7). Bottom panel: Time course of total enzyme simulated with eqs. 1 and 2 for eventual steady-state I/Ki of 0.1, 1, 2, and 3. In the time course simulations, inhibitor/inducer is infused from 0 to 350 hr.

The time course of induction of total enzyme from the beginning of the infusion of inhibitor/inducer to the return of enzyme to the basal state after the end of the infusion also is shown in fig. 4. At low steady-state inducer/inhibitor concentration, I/Ki = 0.1, enzyme induction is minimal and reaches steady-state in 50 hr. As I/Ki increases to 1, enzyme is induced by 50% over the initial value and reaches steady-state by 100 hr (the half-life becomes longer as a greater fraction of the total enzyme is stabilized). When administration of inducer is stopped, enzyme declines as inhibitor/inducer is removed and enzyme is degraded. The pre-induction level of enzyme is reached by 200 hr after the infusion is stopped, consistent with the slow half-life as CYP2E1 has been elevated in pool 2 as well as pool 1. Although, again, 50 hr after inhibitor/inducer infusion is stopped only a modest induction remains due to the influence of the short half-life on removal of CYP2E1. At I/Ki = 3, greater than 2-fold induction of the enzyme is attained at 168 hr. As I/Ki increases, the time required to reach steady-state increases because the greater the fraction of enzyme in pool 1 that is stabilized, the longer is the turnover time of total enzyme. This simulation shows that the time course of the response of enzyme is as expected based on the general scheme of the model.

Clearance Inhibition.

The interaction considered has two components that effect clearance: induction and inhibition. To assure that both are operating in the model as expected, the inhibition component was analyzed before their combined effects on clearance were considered.

The evaluation of the change in substrate clearance caused by the inhibitor/inducer requires a selection of the basal state to which the altered states of the enzyme and clearance are to be compared. As described in the mathematical description of the model, two basal states are relevant. The first, which is referred to as “case 1,” divides the clearance at any time (and any inhibitor/inducer concentration) by the clearance that would be observed if the inhibitor/inducer was suddenly removed and the substrate concentration was unchanged. Thus, in case 1, Cl0 (the basal clearance) is E·kcat/(Km+S).

The second case, “case 2,” uses as basal clearance the value of clearance in the absence of the inhibitor/inducer and at vanishingly low concentration of substrate, i.e. S/Km→0. In this case, Cl0is E·kcat/Km. This basal clearance is identified in the figures as Cl0,(S/Km→0). Case 2 allows evaluation of the net effect of inhibitor/inducer concentration and substrate concentration on substrate clearance in relation to the clearance that usually operates in therapeutics, low substrate concentration relative to Km and no interacting drug.

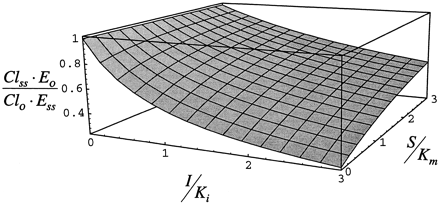
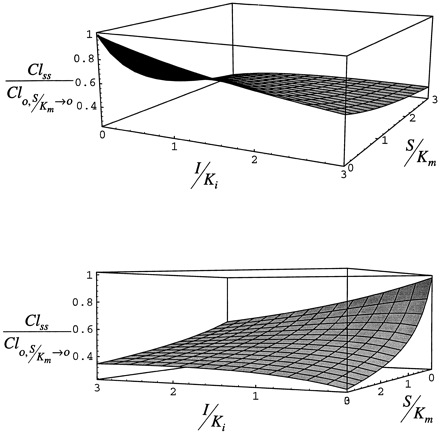
Case 1. The inhibition component of the interaction, Cl/E, as described by eq. 10 is shown in fig.5. For this case, at I/Ki = 0, Cl0/E0 is 1 by definition at all values of S/Km, since Cl0 is defined as E·kcat/(Km+S). At low S/Km, Cl/E decreases as I/Ki increases and inhibition becomes greater. At I/Ki = 3, the enzyme is nearly saturated with inhibitor/inducer. At this value of I/Ki, Cl/E is at the minimum at low S/Km. As S/Km increases, substrate displaces inhibitor/inducer and Cl/E increases in comparison to the clearance in the absence of inhibitor/inducer at the same concentration of substrate.

Figure 5
Figure 5

Steady-state inhibition of clearance (Cl/E) for case 1, simulated by neglecting the accumulation of enzyme due to stabilization as described by eq. 10.

Case 2.

In fig. 6, the inhibition component of clearance, Cl/E, is shown as described by eq. 11. At low S/Km, Cl/E decreases as I/Ki increases (due to inhibition) and as S/Km increases (due to saturation of the enzyme with substrate) at low I/Ki. When I/Ki = 3, the enzyme is bound with inhibitor/inducer and Cl/E declines slightly as S/Km increases because the enzyme becomes saturated with substrate as inhibitor/inducer is displaced. Cl/E is minimum as both S/Km and I/Ki increase to 3.

Figure 6
Figure 6

Steady-state inhibited clearance (Cl/E) for case 2, simulated by neglecting the accumulation of enzyme due to stabilization as described by eq. 11.

The lower panel is a 180° rotation of the upper panel.

Combined Effects of Inhibition and Induction on Substrate Clearance at Steady-State

The simulations presented in this section consider the situation in which inhibitor/inducer has been infused to steady-state and is continued as the combined effects of induction and inhibition on substrate clearance are evaluated. The two cases of expression of the alteration of clearance are included as above.

Case 1.

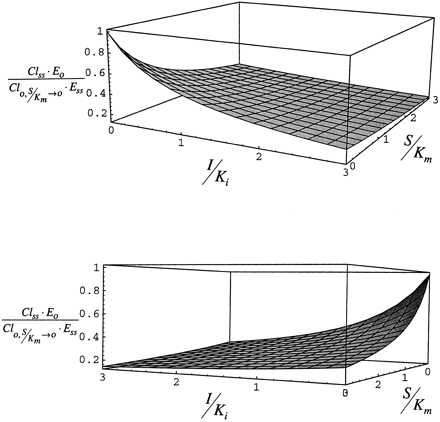
Fig. 7 shows the effect of the administration of inhibitor/inducer on the clearance of substrate expressed relative to clearance at the same concentration of substrate. When S/Km is approximately 0 and I/Ki increases, clearance decreases. Thus, at low substrate concentration the net effect of the inhibitor/inducer is inhibition of clearance as the low concentration of substrate cannot displace inhibitor/inducer from the enzyme. As S/Km is increased at I/Ki = 3, substrate can displace inhibitor/inducer and clearance rises. As S/Km approaches I/Ki, clearance becomes greater than that observed at the same concentration of substrate in the absence of inhibitor/inducer.

Figure 7
Figure 7

Steady-state clearance simulated with eq. 8for case 1.

The upper panel is a three-dimensional view, and thelower panel is a two-dimensional view that illustrates the ability of the substrate to compete for the enzyme as I/Ki is increased at any value of S/Km.

Case 2.

Fig. 8 shows the effect of the administration of inhibitor/inducer on the clearance of substrate expressed relative to clearance at vanishingly low substrate concentration. By definition in this case, Cl(t)/Cl0 declines as either I/Ki or S/Km increases. The most important result of this simulation is the illustration that the condition in which maximum substrate clearance will be observed is when inhibitor/inducer is absent and substrate concentration is low. In other words, as long as the inhibitor/inducer is present, clearance will not rise above the value observed in its absence at low substrate concentration even though the enzyme is induced. Although increasing substrate concentration will displace inhibitor/inducer from the enzyme (this result is apparent in case 1), the net effect of increasing substrate concentration is to saturate the enzyme and decrease clearance in comparison to the value observed at vanishingly low substrate concentration in the absence of inhibitor/inducer.

Figure 8
Figure 8

Steady-state clearance simulated with eq. 9for case 2.

The lower panel is a 180° rotation of the upper panel.

Time Course of Inhibition/Induction of Substrate Clearance as Inhibitor/Inducer is Added and Removed

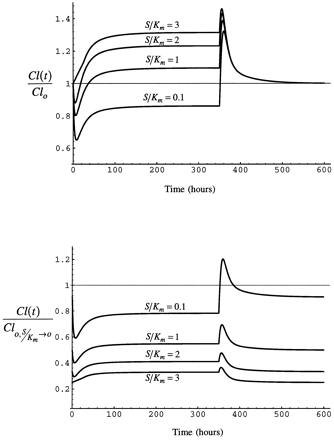
The time course of substrate clearance over the entire period of exposure to inhibitor/inducer and the decline of enzyme to the basal level after inhibitor/inducer is removed is examined in this section. Fig. 9 shows the results for both cases of clearance for different values of S/Km at a steady-state I/Ki of 1.3

Figure 9
Figure 9

Upper panel: Time course of clearance as simulated for case 1 with eq. 5 during and after a 350 hr infusion of inhibitor/inducer. Lower panel: Time course of clearance as simulated for case 2 with eq. 6 during and after a 350 hr infusion of inhibitor/inducer.

S/Km is varied as shown at a constant (eventual) steady-state I/Ki of 1.

Case 1.

As inhibitor/inducer is introduced by constant rate infusion, clearance of substrate declines. The decline in substrate clearance is greater at the low values of S/Km, as competitive inhibition is greater when substrate concentration is lower. Substrate clearance increases over the period of infusion of inhibitor/inducer as the enzyme accumulates as a consequence of stabilization. At the end of the 350 hour infusion, substrate clearance rapidly increases as inhibitor/inducer concentration declines. The increase is greatest when S/Km is low because competitive inhibition is greatest at low S/Km and induction is a function only of inhibitor/inducer concentration, which did not vary among the simulations. The enzyme returns to the pre-induction value by 200 hr after the infusion is stopped.

Case 2.

As in case 1, substrate clearance declines as inhibitor/inducer is introduced. The decline is greatest when S/Km is 0.1 because of saturation of the enzyme by high substrate concentration. As the infusion of inhibitor/inducer is continued, clearance of substrate increases somewhat as enzyme accumulates as a consequence of stabilization. At the end of the infusion of inhibitor/inducer, clearance of substrate increases quickly as inhibitor/inducer is eliminated. The increase is most pronounced in this case when S/Km is small because the enzyme is not saturated with substrate and the degree of competitive inhibition is greatest when S/Km is low.

Fig. 10 shows the results for both expressions of the change in clearance for different values of I/Ki at S/Km of 0.1. In these simulations, the behavior of case 1 and case 2 are similar. As administration of inhibitor/inducer is initiated, substrate clearance falls as a consequence of inhibition, with the greatest decline when I/Ki is greatest. As administration of inhibitor/inducer continues, clearance rises as enzyme accumulates. At the end of the infusion of inhibitor/inducer, clearance rises abruptly as inhibitor/inducer is eliminated. The magnitude of the rise is greatest when I/Ki is greatest, as this is the condition in which induction was maximal.

Figure 10
Figure 10

Upper panel: Time course of clearance as simulated for case 1 with eq. 5 during and after a 350 hr infusion of inhibitor/inducer. Lower panel: Time course of clearance as simulated for case 2 with eq. 6 during and after a 350 hr infusion of inhibitor/inducer.

Eventual steady-state I/Ki is varied as S/Km is held constant at 0.1.

Comparison of Model Predictions with Experimental Results

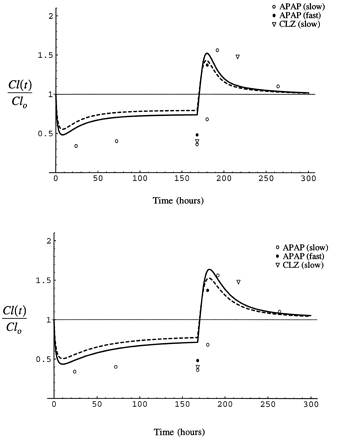
Fig. 11 shows the results of a simulation of the time course of the interaction between isoniazid and acetaminophen as predicted by the model in comparison to data from a series of clinical studies of the effect of isoniazid administration on the formation of NAPQI from acetaminophen and 6-hydroxychlorzoxazone from chlorzoxazone, both CYP2E1-modulated events (26-28). In each study, 300 mg isoniazid was administered once a day for several days and 500 mg acetaminophen or 750 mg chlorzoxazone was administered on three occasions, either before isoniazid was begun (26, 27) or well after the induction of CYP2E1 by isoniazid had reversed (1–2 weeks) (28), during isoniazid administration, and some time soon after the administration of isoniazid had been stopped (26-27). When given during the course of isoniazid administration, acetaminophen was usually given simultaneously with isoniazid (26, 27). In one study however (28), acetaminophen was given either with isoniazid in the morning or 12 hr after the morning dose of isoniazid. In that study, the time course of reversal of the interaction from inhibited to enhanced formation of NAPQI was evaluated as a function of isoniazid acetylator phenotype.

Figure 11
Figure 11

Simulation of the time course of the interaction between isoniazid and acetaminophen or chlorzoxazone assuming I/Ki of 1.5, (stippled line) and 2.0 (solid line). S/Km = 0.1 in all simulations.

Top panel, CYP2E1 half-lives of 7 and 37 hr, bottom panel, 15 and 79 hr. Circles represent data from studies of the formation of NAPQI from acetaminophen (26-28) and triangles the formation of 6-hydroxychlorzoxazone from chlorzoxazone (27). Open symbols represent slow acetylators of isoniazid and closed symbols rapid acetylators. In each study, isoniazid was administered as 300 mg once daily in the morning for several days. Acetaminophen (500 mg) and chlorzoxazone (750 mg) were administered before isoniazid was begun (26-27) or well after CYP2E1 induction had reversed after isoniazid (28), during the period of administration of isoniazid, and shortly after isoniazid was stopped. Acetaminophen (26-27) and chlorzoxazone (27) were given together with isoniazid during the period of isoniazid administration, except in one case in which acetaminophen was either given together with isoniazid or 12 hr after the dose of isoniazid (28).

The simulations in fig. 11 take a value of S/Kmof 0.1. In humans, the dose of acetaminophen administered produces a maximum concentration in plasma of approximately 56 μM (28) and the dose of chlorzoxazone a maximum unbound concentration of 3 μM (55). The Km of acetaminophen for CYP2E1 is approximately 1 mM (56), and that for chlorzoxazone is 45 μM in human liver microsomes (42, 57). The half-lives of CYP2E1 have been established in the rat, but not in humans. In addition to conducting simulations with CYP2E1 half-lives of 7 and 37 hr as observed in the rat, we also performed simulations with values of 15 and 79 hr, as the half-life in humans is expected to be longer than rat. Also, the time for alcoholics to return to an uninduced CYP2E1 activity has been estimated to be 60 hr (58). The longer half-life values used provide the same distribution of enzyme between the two pools we estimated in the rat. Peak isoniazid concentration in plasma is reported to vary between 36 and 73 μM at a dose of 300 mg (59, 60), and a Ki of 40 μM for human CYP2E1 has been reported (53).

Fig. 11 shows data from the human studies and simulations with the literature parameters for I/Ki of 1.5 and 2, and CYP2E1 half-lives of 7 and 37 hr and 15 and 79 hr. The simulation with the longer half-lives and larger I/Ki best fit the data, although both agree qualitatively well with the time course of the interaction, inhibited clearance giving way to enhanced clearance.

Discussion

We have described a model of the time course of CYP2E1 inhibition/induction drug interactions that are a consequence of stabilization of the enzyme by bound ligand. The model accurately describes the biphasic degradation of enzyme that is observed in the absence of an inhibitor/inducer and the monophasic decline when the inhibitor/inducer is present. The degree of inhibition and induction is a function of inhibitor/inducer concentration and its affinity for the enzyme, while substrate concentration and Kminfluence the degree of inhibition as described by the competitive mechanism. Although the interaction is complex, the model suggests that the time course of the interaction and its magnitude can be anticipated from measurements made in vitro and knowledge of CYP2E1 half-lives and distribution between pools.

The effects of the inhibitor/inducer on the clearance of CYP2E1 substrates were examined by considering two separate baseline values of clearance, either that at the respective concentration of substrate in the absence of the inhibitor/inducer, or that at vanishingly low substrate concentration (S/Km≪1). It is clear from the former case that the magnitude of decrease in substrate clearance when the inhibitor/inducer is present is less than would be the case if induction had not occurred. The second case illustrates that at steady-state, in the presence of uninterrupted administration of the inhibitor/inducer, it is not possible to raise substrate concentration high enough to increase clearance above the value observed in the absence of the inhibitor/inducer and at low substrate concentration. While increasing substrate concentration reverses competitive inhibition it also saturates enzyme, resulting in diminished clearance in comparison to low substrate concentration.

On the other hand, it is also apparent that enhanced clearance is observed when inhibitor/inducer administration is discontinued and inhibitor/inducer is eliminated more quickly than CYP2E1. Thus, the model predictions are also generally consistent with the reversal from inhibited to enhanced NAPQI formation within the 24 hr dosing interval that we have observed in rapid acetylators of isoniazid in comparison with slow acetylators (28). Also, the model simulations are consistent with observations of the isoniazid-chlorzoxazone interaction reported by O’Shea et al. (30), in which an enhanced formation of 6-hydroxychlorzoxazone was observed in slow acetylators 2 days after the last dose of isoniazid but not in rapid acetylators. In the latter case, 6-hydroxychlorzoxazone formation at the same time had returned to the value observed in the absence of isoniazid. In both cases, the extent of inhibition and induction is generally underpredicted. The underprediction may indicate a contribution to the modulation of CYP2E1 by the hydrazine metabolites of isoniazid (53, 61-62).

Another interaction that occurs at least in part through the mechanism of substrate stabilization and seems to be of clinical significance is that between acetaminophen and ethanol (29). It is clear from these studies and the effects of ethanol on enflurane metabolism in rabbits that the formation clearance of NAPQI can be both inhibited and induced by ethanol. Thus, it would seem that simultaneous ingestion of ethanol with acetaminophen would tend to be protective against NAPQI-induced hepatotoxicity (63), while ingestion of acetaminophen when ethanol concentration has declined in the presence of CYP2E1 induction would be expected to enhance exposure to NAPQI. Derangements of glutathione homeostasis and UDP-glucuronic acid availability in the presence of fasting and alcoholic liver damage may alter these expectations (64,65).

To obtain biphasic elimination kinetics of CYP2E1 in the absence of the inhibitor/inducer in the model, it was necessary to incorporate two physically distinct pools of the enzyme into the model. The two pools share one mechanism (the slow mechanism) of enzyme degradation, but only one pool, the one into which new enzyme is synthesized, contains enzyme that is degraded by the rapid mechanism. Transfer of the enzyme from one pool to the other or binding of ligand protects enzyme from the rapid phase of degradation. Consideration of the known intracellular distribution suggested to us that the two pools might be the rough and smooth endoplasmic reticulum. However, it has not been demonstrated that a rapid degradation process operates at only one of these sites, while the slow process operates at both. Results of these simulations regarding the different time course and extent of induction in the two pools may be useful in identifying the actual pools.

The class of drug interactions that accrue through ligand stabilization of CYP2E1 may be unique to this enzyme.4 They represent an unusual case in which the effect of one drug on the other is not inhibition or induction, but both. The net result of the effect of the inhibitor/inducer on the clearance of the substrate is predictable from the synthesis and degradation kinetics of the enzyme and the affinities and concentrations of the inhibitor/inducer and substrate. The unusual feature of this interaction is that although induction of CYP2E1 begins as soon as the inhibitor/inducer is administered, enhanced clearance of substrate in relation to the pre-inhibitor/inducer condition is observed only after the inducer is removed. The isoniazid-acetaminophen interaction illustrates that it is possible for the interaction to cycle between inhibited and enhanced clearance within a dosing interval of the inhibitor/inducer. A detailed understanding of the pharmacokinetic consequences of this mechanism of interaction is likely to aid the interpretation of drug interaction studies involving CYP2E1.

Footnotes

  • Send reprint requests to: John T. Slattery, Ph.D., Department of Pharmaceutics, Box 357610, University of Washington, Seattle, WA 98195-7610. E-mail: jts{at}u.washington.edu.

  • This work was supported in part by grants GM 32165 and GM 48349 from the National Institutes of Health.

  • ↵2 Since the inducing ligand induces a spin-shift consistent with occupation of the active site (36), the mechanism of inhibition most likely is competitive, as has been demonstrated with isoniazid in human liver microsomes and in a reconstituted system with expressed CYP2E1 (53). The equations for fu and fb are derived from Scatchard’s equilibrium binding equations (54).

  • ↵3 For ease of comparison to steady-state simulations, the time course simulations are identified with values of I/Ki achieved at steady-state. Infusion rate of inhibitor/inducer was varied to achieve the indicated steady-state I/Ki; I/Ki did change over the course of infusion.

  • ↵4 Induction of CYP3A isoforms byN-substituted imidazoles and macrolides may represent variants of this mechanism (66-68).

  • Abbreviations used are::
    CYP2E1
    cytochrome P450 2E1
    NAPQI
    N-acetyl-p-benzoquinone imine
    • Received March 31, 1997.
    • Accepted June 19, 1997.

References

  1. ↵
    1. Koop D. R.,
    2. Crump B. L.,
    3. Nordblom G. D.,
    4. Coon M. J.
    (1985) Immunochemical evidence for induction of the alcohol-oxidizing cytochrome P-450 of rabbit liver microsomes by diverse agents: ethanol, imidazole, trichloroethylene, acetone, pyrazole, and isoniazid. Proc. Natl. Acad. Sci. USA 82:4065–4069.
    OpenUrlAbstract/FREE Full Text
  2. ↵
    1. Ryan D. E.,
    2. Ramanathan L.,
    3. Iida S.,
    4. Thomas P. E.,
    5. Haniu M.,
    6. Shively J. E.,
    7. Lieber C. S.,
    8. Levin W.
    (1985) Characterization of a major form of rat hepatic microsomal Cytochrome P-450 induced by isoniazid. J. Biol. Chem. 260:6385–6393.
    OpenUrlAbstract/FREE Full Text
  3. ↵
    1. Ueno T.,
    2. Gonzalez F. J.
    (1990) Transcriptional control of the rat hepatic CYP2E1 gene. Mol. Cell Biol. 10:4495–4505.
    OpenUrlAbstract/FREE Full Text
  4. ↵
    1. Wu D.,
    2. Cederbaum A. I.
    (1996) Expression of cytochrome P4502E1 in rat fetal hepatocyte culture. Mol. Pharmacol. 49:802–807.
    OpenUrlAbstract
  5. ↵
    1. Wu D.,
    2. Cederbaum A. I.
    (1993) Ethanol consumption by the nursing mother induces cytochrome P-4502E1 in neonatal rat liver. J. Pharmacol. Exp. Ther. 267:560–566.
    OpenUrlAbstract/FREE Full Text
  6. ↵
    1. Johansson I.,
    2. Ekstrom G.,
    3. Scholte B.,
    4. Puzycki D.,
    5. Jornvall H.,
    6. Ingelman-Sundberg M.
    (1988) Ethanol-, fasting-, and acetone-induced cytochromes P-450 in rat liver: regulation and characteristics of enzymes belonging to the IIB and IIE gene subfamilies. Biochemistry 27:1925–1934.
    OpenUrlCrossRefPubMed
  7. ↵
    1. Raucy J. L.,
    2. Lasker J. M.,
    3. Kraner J. C.,
    4. Salazar D. E.,
    5. Lieber C. S.,
    6. Corcoran G. B.
    (1991) Induction of cytochrome P450IIE1 in the obese overfed rats. Mol. Pharmacol. 39:275–280.
    OpenUrlAbstract
  8. ↵
    1. O’Shea D.,
    2. Davis S. N.,
    3. Kim R. B.,
    4. Wilkinson G. R.
    (1994) Effect of fasting and obesity in humans on the 6-hydroxylation of chlorzoxazone: a putative probe of CYP2E1 activity. Clin. Pharmacol. Ther. 56:359–367.
    OpenUrlCrossRefPubMed
  9. ↵
    1. Dong Z.,
    2. Hong J.,
    3. Ma Q.,
    4. Li D.,
    5. Bullock J.,
    6. Gonzalez F. J.,
    7. Park S. S.,
    8. Gelboin H. V.,
    9. Yang C. S.
    (1988) Mechanism of induction of cytochrome P-450ac (P-450j) in chemically induced and spontaneously diabetic rats. Arch. Biochem. Biophys. 263:29–35.
    OpenUrlCrossRefPubMed
  10. ↵
    1. Ma Q.,
    2. Dannan G. A.,
    3. Guengerich F. P.,
    4. Yang C. S.
    (1989) Similarities and differences in the regulation of hepatic cytochrome P-450 enzymes by diabetes and fasting in male rats. Biochem. Pharmcol. 38:3179–3184.
    OpenUrlCrossRefPubMed
  11. ↵
    F. J. Gonzalez, T. Ueno, M. Umeno, B. J. Song, R. L. Veech, H. V. Gelboin: Microsomal ethanol oxidizing system: transcriptional and posttranscriptional regulation of cytochrome P450.Alcohol Alcohol. Suppl. 1, 97–101 (1991)..
  12. ↵
    1. Song B. J.,
    2. Matsunaga T.,
    3. Hardwick J. P.,
    4. Park S. S.,
    5. Veech R. L.,
    6. Yang C. S.,
    7. Gelboin H. V.,
    8. Gonzalez F. J.
    (1987) Stabilization of cytochrome P450j messenger ribonucleic acid in the diabetic rat. Mol. Endocrinol. 1:542–547.
    OpenUrlCrossRefPubMed
  13. ↵
    1. Song B. J.,
    2. Veech R. L.,
    3. Park S. S.,
    4. Gelboin H. V.,
    5. Gonzalez F. J.
    (1988) Structure and regulation of the ethanol-inducible cytochrome P450j. Adv. Alcohol Subst. Abuse 7:205–207.
    OpenUrlPubMed
  14. ↵
    1. Song B. J.,
    2. Veech R. L.,
    3. Park S. S.,
    4. Gelboin H. V.,
    5. Gonzelez F. J.
    (1988) Induction of rat hepatic N-nitrosodimethylamine demethylase by acetone is due to protein stabilization. J. Biol. Chem. 264:3568–3572.
    OpenUrlAbstract/FREE Full Text
  15. ↵
    1. Kim S. G.,
    2. Novak R. F.
    (1990) Induction of rat hepatic P450IIE1 (CYP 2E1) by pyridine: evidence for a role of protein synthesis in the absence of transcriptional activation. Biochem. Biophys. Res. Comm. 166:1072–1079.
    OpenUrlCrossRefPubMed
  16. ↵
    1. Park K. S.,
    2. Sohn D. H.,
    3. Veech R. L.,
    4. Song B. J.
    (1993) Translational activation of ethanol-inducible cytochrome P450 (CYP2E1) by isoniazid. Eur. J. Pharmacol. 248:7–14.
    OpenUrlPubMed
  17. ↵
    1. Raha A.,
    2. Reddy V.,
    3. Houser W.,
    4. Bresnick E.
    (1990) Binding characteristics of 4S PAH-binding protein and Ah receptor from rats and mice. J. Toxicol. Environ. Health. 29:339–355.
    OpenUrlCrossRefPubMed
  18. ↵
    1. Okey A. B.
    (1990) Enzyme induction in the cytochrome P-450 system. Pharmacol. Ther. 45:241–298.
    OpenUrlCrossRefPubMed
  19. ↵
    1. Neuhold L. A.,
    2. Shirayoshi Y.,
    3. Ozato-K K.,
    4. Jones J. E.,
    5. Nebert D. W.
    (1989) Regulation of mouse CYP1A1 gene expression by dioxin: requirement of two cis-acting elements during induction. Mol. Cell Biol. 9:2378–2386.
    OpenUrlAbstract/FREE Full Text
  20. ↵
    1. Fisher J. M.,
    2. Jones K. W.,
    3. Whitlock J. P., Jr.
    (1989) Activation of transcription as a general mechanism of 2,3,7,8-tetrachlorodibenzo-p-dioxin action. Mol. Carcinogen. 1:216–221.
    OpenUrlPubMed
  21. ↵
    1. Levy R. H.,
    2. Lai A. A.,
    3. Dumain M. S.
    (1979) Time-dependent kinetics IV: pharmacokinetic theory of enzyme induction. J. Pharm. Sci. 68:398–399.
    OpenUrlCrossRefPubMed
  22. ↵
    1. Levy R. H.
    (1982) Time-dependent pharmacokinetics. Pharmacol. Ther. 17:383–397.
    OpenUrlCrossRefPubMed
  23. ↵
    1. Levy R. H.,
    2. Dumain M. S.,
    3. Cook J. L.
    (1979) Time-dependent kinetics V: time course of drug levels during enzyme induction (one-compartment model). J. Pharm. Biopharm. 7:557–578.
    OpenUrlCrossRef
  24. ↵
    1. Ryan D. E.,
    2. Koop D. R.,
    3. Thomas P. E.,
    4. Coon M. J.,
    5. Levin W.
    (1986) Evidence that isoniazid and ethanol induce the same microsomal cytochrome P-450 in rat liver, an isozyme homologous to rabbit liver cytochrome P-450 isozyme 3a. Arch. Biochem. Biophys. 246:633–644.
    OpenUrlCrossRefPubMed
  25. ↵
    1. Koop D. R.,
    2. Morgan E. T.,
    3. Tarr G. E.,
    4. Coon M. J.
    (1982) Purification and characterization of a unique isozyme of cytochrome P-450 from liver microsomes of ethanol-treated rabbits. J. Biol. Chem. 257:8472–8480.
    OpenUrlAbstract/FREE Full Text
  26. ↵
    1. Epstein M. M.,
    2. Nelson S. D.,
    3. Slattery J. T.,
    4. Kalhorn T. F.,
    5. Wall R. A.,
    6. Wright J. M.
    (1991) Inhibition of the metabolism of paracetamol by isoniazid. Br. J. Clin. Pharmacol. 31:139–142.
    OpenUrlPubMed
  27. ↵
    1. Zand R.,
    2. Nelson S. D.,
    3. Slattery J. T.,
    4. Thummel K. E.,
    5. Kalhorn T. F.,
    6. Adams S S.,
    7. Wright J. M.
    (1993) Inhibition and induction of cytochrome P450 2E1-catalyzed oxidations by isoniazid in humans. Clin. Pharmacol. Ther. 54:142–149.
    OpenUrlPubMed
  28. ↵
    1. Chien J. Y.,
    2. Peter R. M.,
    3. Nolan C. M.,
    4. Wartelle C.,
    5. Slattery J. T.,
    6. Nelson S. D.,
    7. Carithers R. L., Jr.,
    8. Thummel K. E.
    (1997) Influence of polymorphic N-acetyltransferase phenotype on the inhibition and induction of acetaminophen bioactivation with long-term isoniazid. Clin. Pharmacol. Ther. 61:24–34.
    OpenUrlCrossRefPubMed
  29. ↵
    1. Slattery J. T.,
    2. Nelson S. D.,
    3. Thummel K. E.
    (1996) The complex interaction between ethanol and acetaminophen. Clin. Pharm. Ther. 60:241–246.
    OpenUrlCrossRefPubMed
  30. ↵
    1. O’Shea D.,
    2. Rim R. B.,
    3. Wilkinson G. R.
    (1997) Modulation of CYP2EI activity by isoniazid in rapid and slow N-acetylators. Br. J. Clin. Pharmacol. 43:99–103.
    OpenUrlPubMed
  31. ↵
    1. Ronis M. J.,
    2. Huang J.,
    3. Crouch J.,
    4. Mercado C.,
    5. Irby D.,
    6. Valentine C. R.,
    7. Lumpkin C. K.,
    8. Ingelman-Sundberg M.,
    9. Badger T. M.
    (1993) Cytochrome P450 CYP 2E1 induction during chronic alcohol exposure occurs by a two-step mechanism associated with blood alcohol concentrations in rats. J. Pharmacol. Exp. Ther. 264:944–950.
    OpenUrlAbstract/FREE Full Text
  32. ↵
    1. Badger T. M.,
    2. Ronis M. J.,
    3. Ingelman-Sundberg M.,
    4. Hakkak R.
    (1993) Pulsatile blood alcohol and CYP2E1 induction during chronic alcohol infusions in rats. Alcohol 10:453–457.
    OpenUrlCrossRefPubMed
  33. ↵
    1. Rice S. A.,
    2. Sbordone L.,
    3. Mazze R. I.
    (1980) Metabolism by rat hepatic microsomes of fluorinated ether anesthetics following isoniazid administration. Anesthesiology 53:489–493.
    OpenUrlPubMed
  34. ↵
    1. Roberts B. J.,
    2. Song B. J.,
    3. Soh Y.,
    4. Park S. S.,
    5. Shoaf S. E.
    (1995) Ethanol induces CYP2E1 by protein stabilization. Role of ubiquitin conjugation in the rapid degradation of CYP2E1. J. Biol. Chem. 270:29632–29635.
    OpenUrlAbstract/FREE Full Text
  35. ↵
    1. Tsutumi M.,
    2. Lasker J. M.,
    3. Takahashi T.,
    4. Lieber C. S.
    (1993) In vivo induction of hepatic P4502E1 by ethanol: role of increased enzyme synthesis. Arch. Biochem. Biophys. 304:209–216.
    OpenUrlCrossRefPubMed
  36. ↵
    1. Eliasson E.,
    2. Johansson I.,
    3. Ingelman-Sundberg M.
    (1988) Ligand-dependent maintenance of ethanol-inducible cytochrome P-450 in primary rat hepatocyte cell cultures. Biochem. Biophys. Res. Comm. 150:436–443.
    OpenUrlCrossRefPubMed
  37. ↵
    1. Pantuck E. J.,
    2. Pantuck C. B.,
    3. Ryan D. E.,
    4. Conney A. H.
    (1985) Inhibition and stimulation of enflurane metabolism in the rat following a single dose or chronic administration of ethanol. Anesthesiology 62:255–262.
    OpenUrlCrossRefPubMed
  38. ↵
    1. Kharasch E. D.,
    2. Thummel K. E.,
    3. Mautz D.,
    4. Bosse S.
    (1994) Clinical enflurane metabolism by cytochrome P450 2E1. Clin. Pharmacol. Ther. 55:434–440.
    OpenUrlPubMed
  39. ↵
    1. Thummel K. E.,
    2. Kharasch E. D.,
    3. Podoll T.,
    4. Kunze K.
    (1993) Human liver microsomal enflurane defluorination catalyzed by cytochrome P-450 2E1. Drug Metab. Dispos. 21:350–357.
    OpenUrlAbstract
  40. ↵
    1. Page A. D.,
    2. Carlson P. G.
    (1994) The effect of pyridine on the in vitro and in vivo metabolism of ethyl carbamate (urethane) by rat and mouse. Carcinogenesis 15:2177–2181.
    OpenUrlAbstract/FREE Full Text
  41. ↵
    1. Raucy J. L.,
    2. Lasker J. M.,
    3. Lieber C. S.,
    4. Black M.
    (1989) Acetaminophen activation by human liver cytochromes P450IIE1 and P450IA2. Arch. Biochem. Biophys. 271:270–283.
    OpenUrlCrossRefPubMed
  42. ↵
    1. Peter R.,
    2. Bocker R.,
    3. Beaune P. H.,
    4. Iwasaki M.,
    5. Guengerich F. P.,
    6. Yang C. S.
    (1990) Hydroxylation of chlorzoxazone as a specific probe for human liver cytochrome P-450IIE1. Chem. Res. Toxicol. 3:566–573.
    OpenUrlCrossRefPubMed
  43. ↵
    1. Sarich T.,
    2. Kalhorn T.,
    3. Magee S.,
    4. Al-Sayegh F.,
    5. Adams S.,
    6. Slattery J.,
    7. Goldstein J.,
    8. Nelson S.,
    9. Wright J.
    (1997) The effect of omeprazole pretreatment on acetaminophen metabolism in rapid and slow metabolizers of S-mephenytoin. Clin. Pharmacol. Ther. 62:21–28.
    OpenUrlCrossRefPubMed
  44. ↵
    1. Tierney D. J.,
    2. Haas A. L.,
    3. Koop D. R.
    (1992) Degradation of cytochrome P450 2E1: selective loss after labilization of the enzyme. Arch. Biochem. Biophys. 293:9–16.
    OpenUrlCrossRefPubMed
  45. ↵
    1. Johansson I.,
    2. Eliasson E.,
    3. Ingelman-Sundberg M.
    (1991) Hormone controlled phosphorylation and degradation of CYP2B1 and CYP2E1 in isolated rat hepatocyte. Biophys. Res. Comm. 174:37–42.
  46. ↵
    1. Eliasson E.,
    2. Johansson I.,
    3. Ingelman-Sundberg M.
    (1990) Substrate-, hormone-, and cAMP-regulated cytochrome P450 degradation. Proc. Natl. Acad. Sci. USA 87:3225–3229.
    OpenUrlAbstract/FREE Full Text
  47. ↵
    1. Eliasson E.,
    2. Mkrtchian S.,
    3. Ingelman-Sundberg M.
    (1992) Hormone- and substrate-regulated intracellular degradation of cytochrome P450 (2E1) involving MgATP-activated rapid proteolysis in the endoplasmic reticulum membranes. J. Biol. Chem. 267:15765–15769.
    OpenUrlAbstract/FREE Full Text
  48. ↵
    1. Neve E. P. A.,
    2. Eliasson E.,
    3. Pronzato M. A.,
    4. Albano E.,
    5. Marinari U.,
    6. Ingelman-Sundberg M.
    (1996) Enzyme-specific transport of rat liver cytochrome P450 to the Golgi apparatus. Arch. Biochem. Biophys. 333:459–465.
    OpenUrlCrossRefPubMed
  49. ↵
    1. Fukui Y.,
    2. Yamamoto A.,
    3. Masaki R.,
    4. Miyauchi K.,
    5. Tashiro Y.
    (1992) Quantitative immunocytochemical analysis of the induction of cytochrome P450IIB in rat hepatocytes. J. Histochem. Cytochem. 40:73–82.
    OpenUrlAbstract/FREE Full Text
  50. ↵
    1. Fujii-Kuriyama Y.,
    2. Negishi M.,
    3. Midawa R.,
    4. Tashiro Y.
    (1997) Biosynthesis of cytochrome P-450 on membrane-bound ribosomes and its subsequent incorporation into rough and smooth microsomes in rat hepatocytes. J. Cell Biol. 81:510–519.
    OpenUrlAbstract/FREE Full Text
  51. ↵
    1. Bradshaw R. A.
    (1989) Protein translocation and turnover in eukaryotic cells. Trends Biochem. Sci. 14:276–279.
    OpenUrlCrossRefPubMed
  52. ↵
    1. Sarate J.,
    2. Kuismanen E.
    (1992) Pathways of protein sorting and membrane traffic between the rough endoplasmic reticulum and the Golgi complex. Semin. Cell Biol. 3:343–355.
    OpenUrlCrossRefPubMed
  53. ↵
    1. Peter R. M.,
    2. Chen W.,
    3. Darbyshire J. F.,
    4. Kunze K. T.,
    5. Nelson S. D.
    (1996) Inhibition of human CYP2E1 and metabolic intermediate complex formation by isoniazid. ISSX Proceedings 10:245.
    OpenUrl
  54. ↵
    1. Segel I. H.
    1. Segel I. H.
    (1993) Rapid equilibrium partial and mixed-type inhibition. in Enzyme Kinetics, ed Segel I. H. (John Wiley, Inc. New York), pp 218–226.
  55. ↵
    1. De Vries J. D.,
    2. Salphati L.,
    3. Horie S.,
    4. Becker C. E.,
    5. Hoener B. A.
    (1994) Variability in the disposition of chlorzoxazone. Biopharm. Drug Disp. 15:587–597.
    OpenUrlCrossRefPubMed
  56. ↵
    1. Patten C. J.,
    2. Thomas P. E.,
    3. Guy R. L.,
    4. Lee M.,
    5. Gonzalez F. J.,
    6. Guengerich F. P.,
    7. Yang C. S.
    (1993) Cytochrome P450 enzymes involved in acetaminophen activation by rat and human liver microsomes and their kinetics. Chem. Res. Toxicol. 6:511–518.
    OpenUrlCrossRefPubMed
  57. ↵
    1. Chen W.,
    2. Peter R. M.,
    3. McArdle S.,
    4. Thummel K. E.,
    5. Sigle R. O.,
    6. Nelson S. D.
    (1996) Baculovirus expression and purification of human and rat cytochrome P450 2E1. Arch. Biochem. Biophys. 331:123–130.
    OpenUrl
  58. ↵
    1. Lucas D.,
    2. M’enez C.,
    3. Girre C.,
    4. Bod’enez P.,
    5. Hispard E.,
    6. M’enez J. F.
    (1995) Decrease in cytochrome P4502E1 as assessed by the rate of chlorzoxazone hydroxylation in alcoholics during the withdrawal phase. Alcohol. Clin. Exp. Res. 19:362–366.
    OpenUrlCrossRefPubMed
  59. ↵
    1. Breda M.,
    2. Pianezzola E.,
    3. Benedetti M. S.,
    4. Efthymiopoulos C.,
    5. Carpentieri M.,
    6. Sassella D.,
    7. Rimoldi R.
    (1992) A study of the effects of rifabutin on isoniazid pharmacokinetics and metabolism in healthy volunteers. Drug Metab. Drug Interact. 10:323–341.
    OpenUrlPubMed
  60. ↵
    1. Weber W. W.,
    2. Hein D. W.
    (1979) Clinical pharmacokinetics of isoniazid. Clin. Pharmacokinet. 4:401–422.
    OpenUrlPubMed
  61. ↵
    1. Jenner A. M.,
    2. Timbrell J. A.
    (1994) Effect of acute and repeated exposure to low doses of hydrazine on hepatic microsomal enzymes and biochemical parameters in vivo. Arch. Toxicol. 68:240–245.
    OpenUrlCrossRefPubMed
  62. ↵
    1. Parthe S.,
    2. Hagmann W.
    (1990) Inhibition of leukotriene w-oxidation by isonicotinic acid hydrazide (isoniazid). Eur. J. Biochem. 187:119–124.
    OpenUrlPubMed
  63. ↵
    1. Critchley J. A.,
    2. Dyson E. H.,
    3. Scott A. W.,
    4. Jarvie D. R.,
    5. Prescott L. F.
    (1983) Is there a place for cimetidine or ethanol in the treatment of paracetamol poisoning? Lancet 2:1375–1376.
    OpenUrl
  64. ↵
    1. Fern’andez-Checa J. C.,
    2. Hirano T.,
    3. Tsukamoto H.,
    4. Kaplowitz N.
    (1993) Mitochondrial glutathione depletion in alcoholic liver disease. Alcohol 10:467–475.
  65. ↵
    1. Whitcomb D. C.,
    2. Block G. D.
    (1994) Association of acetaminophen hepatotoxicity with fasting and ethanol use. JAMA 272:1845–1850.
    OpenUrlCrossRefPubMed
  66. ↵
    1. Ritter J. K.,
    2. Franklin M. R.
    (1987) Induction and inhibition of rat hepatic drug metabolism by N-substituted imidazole drugs. Drug Metab. Dispos. 15:335–343.
    OpenUrlAbstract
  67. ↵
    1. Pappas J. B.,
    2. Franklin M. R.
    (1993) Hepatic clotrimazole concentrations and hepatic drug metabolizing enxyme activities in adult male Sprague-Dawley rats. Toxicology 80:27–35.
    OpenUrlCrossRefPubMed
  68. ↵
    1. Danan G.,
    2. Descatoire V.,
    3. Pessayre D.
    (1981) Self-induction by erythromycin of its own transformation into a metabolite forming and inactive complex with reduced cytochrome P450. J. Pharmacol. Exper. Ther. 218:509–514.
    OpenUrlAbstract/FREE Full Text
Back to top

In this issue

Download PDF
Article Alerts
Email Article
Citation Tools

Research ArticleArticle

Pharmacokinetic Consequences of Induction of CYP2E1 by Ligand Stabilization

Jenny Y. Chien, Kenneth E. Thummel and John T. Slattery
Drug Metabolism and Disposition October 1, 1997, 25 (10) 1165-1175;
Twitter logo Facebook logo Mendeley logo

Jump to section

Related Articles

Cited By...

More in this TOC Section

Similar Articles

Advertisement