Advertisement
Research ArticleArticle

Computational Models for Cytochrome P450: A Predictive Electronic Model for Aromatic Oxidation and Hydrogen Atom Abstraction

Jeffrey P. Jones, Michael Mysinger and Kenneth Ray Korzekwa
Drug Metabolism and Disposition January 2002, 30 (1) 7-12; DOI: https://doi.org/10.1124/dmd.30.1.7

Abstract

Experimental observations suggest that electronic characteristics play a role in the rates of substrate oxidation for cytochrome P450 enzymes. For example, the tendency for oxidation of a certain functional group generally follows the relative stability of the radicals that are formed (e.g., N-dealkylation >O-dealkylation > 2° carbon oxidation > 1° carbon oxidation). In addition, results show that useful correlations between the rates of product formation can be developed using electronic models. In this article, we attempt to determine whether a combined computational model for aromatic and aliphatic hydroxylation can be developed. Toward this goal, we used a combination of experimental data and semiempirical molecular orbital calculations to predicted activation energies for aromatic and aliphatic hydroxylation. The resulting model extends the predictive capacity of our previous aliphatic hydroxylation model to include the second most important group of oxidations, aromatic hydroxylation. The combined model can account for about 83% of the variance in the data for the 20 compounds in the training set and has an error of about 0.7 kcal/mol.

The P4501 enzymes are a superfamily of monooxygenases involved in the metabolism of both exogenous and endogenous compounds. Ironically, these enzymes play a central role in both the prevention and induction of chemical toxicities and carcinogenicity. Although most P450 oxidations of xenobiotics result in detoxification, occasionally a more toxic intermediate is formed. In fact, many ultimate toxins and carcinogens are formed by the bioactivation of less reactive compounds, and many bioactivation reactions are mediated by the P450 enzymes. Often bioactivation reactions are in competition with detoxification pathways for the same substrate. Since these enzymes play such a central role in both detoxification and bioactivation, predictive models for cytochrome P450 catalysis will be useful tools for evaluating of the potential risks of environmental exposures. One of the most pertinent but difficult problems in risk assessment is translating bench results and mechanistic information into a form that can be used. This article outlines steps toward the development of computational models from laboratory data into a form that can be used for risk assessments that accurately reflect experimental results. For example, these models now more completely describe all positions of metabolism for nitriles and should be more complete in predicting the toxicity related to nitrile metabolism. These semiempirical computational models blend experimental data and computational chemistry in such a way as to provide a consistent prediction of the bioactivation rates for a broad spectrum of compounds. In particular, these models can be used to predict xenobiotic metabolism by the P450 enzyme family, including the bioactivation of compounds to toxins and carcinogens.

Models such as those presented here for P450-mediated reactions can also play a role in drug design. Tools that predict regioselectivity can be used to assess the pharmacokinetics of drugs before synthesis, saving time and money in the drug development process. These types of tools, either alone or in combination with homology or pharmacophore models, can also provide for the design of better drugs, with higher compliance and fewer toxic side-effects. However, P450 enzymes are difficult to model by the standard methods used for most drug targets, which are based mainly on predicting binding affinities related to steric features, since accurate results depend upon the prediction of both the electronic and steric features of the enzymes. This is different from many other enzyme systems since P450 has the need to metabolize a vast array of xenobiotics, which makes it impractical to have one enzyme for each compound or even each class of compounds. Therefore, although most cellular functions tend to be very specific, xenobiotic metabolism requires enzymes with diverse substrate specificities. The cytochromes P450 have apparently assumed much of this role. The required diversity is accomplished by families and subfamilies of enzymes with generally broad substrate specificities, a very reactive oxygenating species and a broad regioselectivity. Thus, for many reactions, the electronic features of the substrate are all that are required to predict regioselectivity (Grogan et al., 1992; Harris et al., 1992; de Groot et al., 1995, 1999;Yin et al., 1995).

We have reported a rapid electronic model for the prediction of regioselectivity in P450-mediated hydrogen atom abstraction mechanisms (Korzekwa et al., 1990a). The methods depend only on the calculation of the AM1 ground-state energies for the parent compound and the product radicals. The relative activation energy is predicted by the use of eq.1.ΔHact=2.60+0.22(ΔH)R+2.38(IPrad) Equation 1This model has been successfully used to predict the rates of metabolism of halogenated hydrocarbons (Harris et al., 1992; Yin et al., 1995) and the regioselectivity of nitrile metabolism (Grogan et al., 1992) both in vivo and in vitro. In this article, we report the development of a model for aromatic oxidation and the combination of this model with our previous model for hydrogen atom abstraction. The combined models allow for the prediction of the electronic component for the regioselectivity of most of the reactions catalyzed by the cytochrome P450 superfamily of enzymes. These models are general models for the electronic component of P450 enzymes, which we have shown to be rather constant across both the enzyme families and species (Jones et al., 1990; Karki et al., 1995; Yin et al., 1995; Higgins et al., 1998).

Materials and Methods

Data analysis and graphing were done with SigmaPlot version 5 (SPSS, Inc. Chicago, IL). The energy difference for regioselectivity was determined by taking the log of the ratio of metabolites and multiplying by 0.616, which gives the energetic difference at 310°K.

Semiempirical calculations were performed with Gaussian 98 (Gaussian, Inc., Pittsburgh, PA.). The semiempirical activation energies for hydrogen atom abstraction for the reactions outlined in the text were estimated with our quantum mechanical model [thep-nitrosophenoxy radical (PNR) model] based on hydrogen abstraction reactions using PNR (Korzekwa et al., 1990b) and the semiempirical AM1 Hamiltonian (Dewar et al., 1985). The model uses the calculated (AM1) enthalpies of reaction and the ionization potentials of the resultant radicals to predict the AM1 activation enthalpies (Hact). All open shell systems were treated with an unrestricted Hartree-Fock Hamiltonian. Each of the reactants and the transition states for the aromatic hydroxylation reactions were minimized using the default procedures in Gaussian 98, and each transition state was confirmed by frequency calculations and had only one negative eigenvalue. All transition states were found by following the most negative eigenvalue after the methoxy radical oxygen-aromatic carbon bond in the tetrahedral intermediate was lengthened to 1.95 Å.

The aromatics compounds listed in Table 1were selected to cover a range of electron-donating and electron-withdrawing groups based on Hammett ς values. We emphasized single-ring compounds at the expense of multiple-ring compounds since all of the experimental data were for single-ring-containing compounds. It is possible that a different model will be required for multiple-ring-containing compounds, five-membered rings, and other types of aromatic compounds for which no experimental is available.

View this table:
Table 1

AM1 energies for addition of methoxy radical to aromatic compounds

Results

Ideally, we would be able to use the same oxidant (PNR) to model P450 aromatic addition that we used for hydrogen atom abstraction. We have shown previously that aromatic oxidation is likely to occur by addition of a triplet-like oxygen to form an tetrahedral intermediate (Korzekwa et al., 1989). This tetrahedral intermediate can then rearrange to epoxides, ketones, and phenols. Although addition of the PNR to an aromatic carbon progresses smoothly through a transition state to a tetrahedral intermediate, the electronic state of the tetrahedral intermediate is not the ground state. Thus, the reactions from reactants to products and products to reactants occur on two different potential energy surfaces. In addition to complicating any transition state studies, the value of any Brønsted correlations will be in doubt since the transition states are not necessarily intermediate between products and reactants. Thus, thep-nitrosophenoxy radical alone is not likely to serve as a versatile model for other P450-mediated oxidations, and other small oxygen radicals were tested within the AM1 formalism.

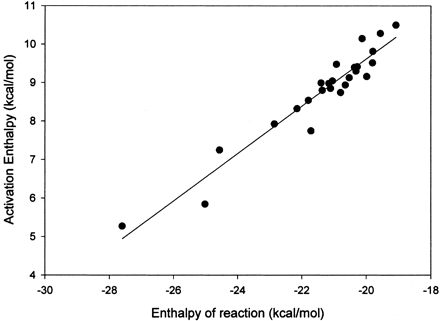
To circumvent the problems associated with PNR additions to aromatic systems, methoxy radical was used for aromatic addition reactions. Using the AM1 formalism, the methoxy radical adds smoothly to aromatic compounds and, in contrast to the p-nitrosophenoxy radical, remains on a single potential energy surface. Methoxy radical was added to the aromatic compounds shown in Table 1, and the heats of reaction and transition state were characterized for each reaction. A good linear correlation was observed for the heats of reaction and the activation energies reported in Table 1. A plot of the data is shown in Fig. 1. Equation 2 is the equation that describes the linear correlation between activation energy and heats of reaction. This linear correlation has aR2 value of 0.92 and a standard error approximately 0.35 kcal/mol. In eq. 2, ΔHact is the enthalpy of activation, and ΔHreac is the enthalpy of reaction. Since this equation depends only on the enthalpy of reaction for predicting rate, even the activation energy of a large compound can be predicted extremely rapidly.ΔHact=21.91+0.61·ΔHreac Equation 2Thus, correlations between computational activation energies and computational heats of reaction can be obtained for both hydrogen abstraction reactions (eq. 1) and aromatic addition reactions (eq. 2) with separate regression models. However, the presence of Brønsted correlations for two different series of reactions does not necessarily imply that the activation energies can be directly compared. For example, the hydrogen atom abstractions are predicted by AM1 to have barriers around 20 kcal/mol, whereas aromatic oxidation has barriers around 10 kcal/mol. Since experimentally hydrogen atom abstraction is found to be favored over aromatic hydroxylation in many instances, these results are quantitatively erroneous. Therefore, a method is required to parameterize the two models to a common energy scale.

Figure 1
Figure 1

The linear correlation of aromatic activation energies and the heats of reaction for formation of a tetrahedral intermediate by methoxy radical.

The R2 value is 0.92, and the 95% confidence limits are shown by the dashed lines.

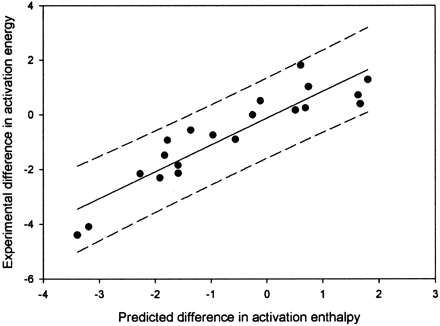
The activation energies of our aliphatic model obtained from eq.1 has never been corrected to reflect experimental activation energies. Thus, we need to scale eq. 1 relative to experimentally measured values. Literature values for regioselectivity that appear to reflect intrinsic reactivity differences were found for octane (Jones et al., 1986, 1990), hexane (Morohashi et al., 1983), diphenylpropane (Hjelmeland et al., 1977a), substituted diphenylpropanes (Hjelmeland et al., 1977b), 2-methylanisole (Higgins et al., 2001), 4-methyanisole (Higgins et al., 2001), α-chloro-p-xylene (Higgins et al., 2001), and ethylbenzene (White et al., 1986). The values for octane, 2-methylanisole, 4-methyanisole, α-chloro-p-xylene, and ethylbenzene have been shown to undergo rapid interchange between the two sites of interest by isotope effect experiments. The octane and hexane values are for C-1 versus C-2 hydroxylation, whereas ethylbenzene and diphenylpropane provide an estimate of the effect of a phenyl substituent on C-1 versus C-2 hydroxylation and benzylic versus an internal secondary position. The remaining compounds give values for substituent effect on benzylic hydroxylation and aromaticO-dealkylation. The computationally predicted energies are given in Table 2. A plot of the predicted versus the observed regioselectivity is given in Fig.2. We performed a linear regression on the experimental versus theoretical data to correct for the differences in predicted versus theoretical regioselectivities, forcing they-intercept through the origin. The results are shown in eq.3.ΔΔGmeasured=0.74·(ΔHact(Habs1)−ΔHact(Habs2)) Equation 3Next, we obtained from the literature different experimentally measured regioselectivity reactions that involved hydrogen atom abstraction and aromatic oxidation. This data are shown in Table3. The methods used for determining the energies have been described previously (Higgins et al., 2001). Ideally, the regioselectivity of reaction is measured in multiple enzymes known to show relatively nonspecific binding. The ratio of two metabolites then is assumed to be a measure of the difference in reactivity. In practice, only a very small number of reported regioselectivity values meet these criteria. The sparse dataset means that as more data becomes available the models are likely to change; however, the approach described here should still be applicable.

View this table:
Table 2

Experimentally measured energy differences in activation energies for aliphatic P450 oxidation reactions

Figure 2
Figure 2

A plot of predicted and measured energy differences for hydrogen atom abstraction from the values given in Table 2.

The R2 value is 0.81, and the 95% confidence limits are shown by the dashed lines.

View this table:
Table 3

Experimentally measured energy differences in activation energies for aromatic and aliphatic P450 oxidation reactions

The metabolism of toluene was determined to give around 70% benzyl alcohol and 30% aromatic hydroxylation in phenobarbital-induced rat microsomes (Hanzlik et al., 1984; Hanzlik and Ling, 1990) and to give 95% benzyl alcohol and 5% aromatic hydroxylation in human microsomes (Tassaneeyakul et al., 1996). These results give differences in energy of activation for the aromatic to benzylic hydroxylation of 0.7 and 1.8 kcal/mol for the two systems, respectively. Since the work done in rat microsomes gave a range of ortho, meta, and para products, we decided to take the mean of the upper and lower limit of the range to fit to the computational results. For ethylbenzene, the reported ratio of para hydroxylation to benzylic hydroxylation in purified CYP2B1 was around 0.0013 with an energy difference of 4.1 kcal/mol, reflecting the faster reaction for the secondary benzylic position relative to the primary benzylic position of toluene (White et al., 1986). Foro-xylene and p-xylene the ratios of benzylic to aromatic were measured to be 11.5 and 33, which correspond to energy differences of 1.5 and 2.2 kcal/mol (Iyer et al., 1997). When a similar experiment was conducted by Lindsey-Smith for anisole metabolism, aromatic oxidation was found to be faster thanO-dealkylation by about 3 times (Lindsay-Smith and Sleath, 1983), corresponding to a difference in energy of 0.67 kcal/mol. This is reduced to a ratio of around 2 for ortho hydroxylation of 2-methylanisole, when the average value of single-expressed enzymes shown to give information about energetics is taken into account (Higgins et al., 2001). Of these experiments, only the work of Higgins et al. (2001) was conducted with the expressed purpose of determining the energy difference between two pathways, although ideally all of the data would be generated in the same enzyme preparation and with the goal of accurately determining the ratios of interest.

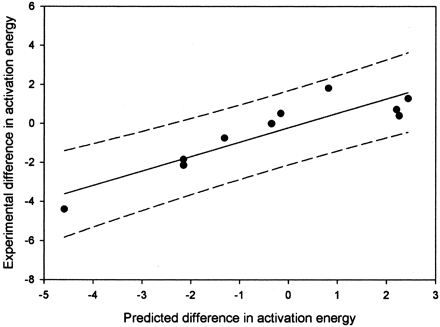
With these data, the model for hydrogen atom abstraction and the new model for aromatic addition can be combined. Figure3 is a plot of the predicted versus measured difference in energy for the oxidations in Table 3. Obviously, a linear relationship exists. The equation for the line is shown in eq.4. In eq. 3, ΔΔGmeasured is the measured difference in energies based on regioselectivity, ΔHact(arom) is the predicted activation energy for aromatic hydroxylation based from eq. 2, and ΔHact(Habs) is the uncorrected AM1 activation energy for hydrogen atom abstraction. The fit eq. 3 gives anR2 value of 0.85, with a standard error approximately 0.65 kcal/mol.ΔΔGmeasured=1.22·(ΔHact(Habs))−1.1·(ΔHact(arom))−17.5 Equation 4Finally, predicted regioselectivity for both eq. 3 and eq. 4 can be plotted together as shown in Fig. 4. The R2 value for the data is 0.83, with a standard error approximately 0.71 kcal/mol.

Figure 3
Figure 3

A plot of the energy predicted differences between aliphatic and aromatic positions versus measured difference in energy for the oxidations in Table 3.

The R2 value is 0.85, and the 95% confidence limits are shown by the dashed lines.

Figure 4
Figure 4

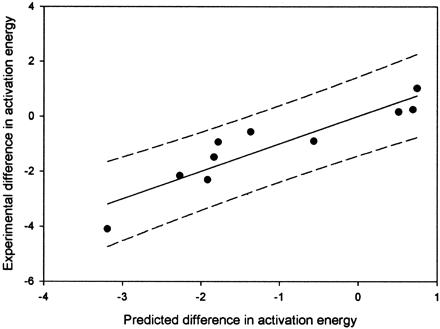
A plot of the predicted versus actual values for the combined aromatic and hydrogen atom abstraction model.

The R2 value is 0.83, and the 95% confidence limits are shown by the dashed lines.

Discussion

Experimental observations suggest that electronic characteristics play a role in the rates of substrate oxidation for cytochrome P450 enzymes. For example, the tendency for oxidation of a certain functional group generally follows the relative stability of the radicals that are formed (e.g., N-dealkylation >O-dealkylation > 2° carbon oxidation > 1° carbon oxidation). In addition, results show that useful correlations between the rates of product formation can be developed using electronic models (Grogan et al., 1992; Yin et al., 1995). These results are apparently contradicted by the results of kinetic experiments, which show the steps before substrate oxidation (electron reduction) to be rate limiting in the catalytic cycle (Higgins et al., 1998). This apparent contradiction can be resolved by an understanding of the kinetics of branched pathways, which was described by Jones et al. (1986). In brief, if product formation is not rate limiting, the reactivity of the substrate will not affect the rate of product formation. However, if an alternate product can be formed, differences in reactivity will be observed. For example, if norcamphor is substituted with deuterium, less product is observed than if it has hydrogen, even though the rate-limiting step is not norcamphor hydroxylation. Atkins and Sligar (1987) found that the isotope effect was observed because the build-up in the enzyme-substrate complex due to deuterium substitution was prevented by alternate product formation. In this case, the alternate product was water. We have seen similar results for the C-1 hydroxylation of octane; however in this case, the alternate products were C-2 and C-3 oxidation products (Jones et al., 1986). Therefore, slowing the rate of oxidation of one position by deuterium substitution causes an increase in the rate of metabolism of another position or an increase in decoupling to water formation (Higgins et al., 1998). This can only occur if the rate of exchange of the different positions within the active site is as fast or faster than the rate of the oxidation step. This means that for a substrate that can rotate freely in the active site the regioselectivity will be primarily determined by the electronic reactivity of the various positions on the molecule (Higgins et al., 2001). For these molecules, product regioselectivities can be predicted by the electronic characteristics of the substrate. Conversely, regioselectivity can provide an important tool for testing computational models.

We previously reported the development of an electronic model for hydrogen atom abstraction with can predict aliphatic hydroxylation, amine dealkylation, and O-dealkylation (Korzekwa et al., 1990a). To our knowledge, this article is the first time anyone has combined predictive models for P450-mediated aromatic and aliphatic oxidation so that a continuous prediction can be made of either aromatic, aliphatic, or a combination of these mechanisms (Fig. 4). However, qualitative models that approach these models have been described for CYP2D6 (de Groot et al., 1999). The model described here was generated by correcting the computational predictions with experimental results for microsomes and single expressed enzymes. Every effort was made to use only experimental data that would be expected to be free of specific enzyme orientation effects, as described by Higgins et al. (2001), and thus should be a general electronic model for cytochrome P450 enzymes. However, we did use a number of data points derived from microsomal preparations. It is possible that the two metabolites in these cases result from two distinct enzymes in the microsomal preparation, and when possible, we chose the phenobarbital-induced microsomal preparation since the major isoform is CYP2B1, an enzyme that has shown a lack of binding preference and a dominance of electronic factors for the type of compounds use in this study (White et al., 1984; Higgins et al., 2001). However, to exclude this data would decrease an already small dataset. In general, we have attempted to construct our electronic models with data for compounds that are small and do not contain strong binding features (Higgins et al., 2001). This means that the best data will not have orienting effects associated with the enzyme tertiary structure. Orienting effects have been shown to be important for a number of P450 enzymes and need to be added to the electronic models for accurate prediction of metabolism by these enzymes (Szklarz and Halpert, 1997; de Groot et al., 1999; Lightfoot et al., 2000; Rao et al., 2000; Szklarz et al., 2000; Xue et al., 2001).

Thus, although this model is general to the P450 superfamily, it is not going to work to any significant extent on enzymes such as those in the 4B family that have a large contribution from substrate-protein interactions determining regioselectivity (Fisher et al., 1998). One might expect the models to work better with enzymes and substrates that show little preference in orientation, such as CYP1A2 (Higgins et al., 2001), CYP2B1 (Higgins et al., 2001), CYP2B4 (White et al., 1984), CYP2E1 (Higgins et al., 2001), and CYP3A4. It should be noted that, although these enzymes have been shown to be free of excessive orientation effects for some substrates, it is possible that other substrates will show strong orientation effects in any one of these enzymes. When binding/orientation effects become large, models that account for binding effects on regioselectivity can be combined with the electronic models to give a more complete description. It is important to note that, although for certain enzymes the electronic model can stand alone to predict regioselectivity, it is doubtful that binding models alone, without an electronic model, can predict regioselectivity. Even strongly orienting P450 enzymes can give multiple products, and the electronic nature of each position must be known.

Other considerations that need to be made when using this model are the general steric accessibility of the positions of interest. For example, octane is metabolized to 1-octanol, 2-octanol, and 3-octanol in the ratio of 1:23:7 (Jones et al., 1990). The model has been shown to predict the correct regioselectivity for the C-1 and C-2 positions; however, the electronics of the C-2 and C-3 position are essentially the same so the 23:7 ratio would not be well predicted. In this case, the C-3 position appears to be less accessible since it is buried in the center of the molecule. Similarly, C-4 hydroxylation is not seen with octane to any appreciable extent, whereas the electronic features are not significantly different from those at the C-2 position. Another feature of this type is ortho hydroxylation. For many compounds, the group adjacent to the ortho position will hinder metabolism at the ortho position. These types of steric shielding are independent of the P450 enzyme and could be added to the models presented here.

Finally, it should be noted that no attempt has been made to externally validate these models. Although this would obviously be preferred, we felt that the datasets were too small to remove data for external validation. We are currently working on developing new datasets to validate these models. We did look at the internal consistency of the models by leave-one-out cross validation and foundq2 values of 0.79 for the combined model (data in Fig. 4). The cross-validatedq2 for leaving out 20% of the data ranged from 0.76 to 0.81 over 10 runs with different randomly chosen groups.

In conclusion, computational models are presented that can predict the two major P450 pathways of metabolism, aliphatic and aromatic oxidation reactions. The models depend on experimental data to correct for the errors associated with the fast semiempirical methods used to predict each reaction mechanism. The computational models corrected by experimentally measured regioselectivities give the predictive models described by eqs. 3 and 4. These models do a reasonable job at predicting the regioselectivity energetics and can be used in conjunction with models for the active site of the enzyme. Studies are underway in the application of these models to predicting human drug metabolism.

Footnotes

  • This work was supported by National Institute of Environmental Health Sciences Grant ES09122.

  • Abbreviations used are::
    P450
    cytochrome P450
    AM1
    Austin model-1
    PNR
    p-nitrosophenoxy radical
    • Received August 20, 2001.
    • Accepted October 1, 2001.

References

  1. ↵
    1. Atkins WM,
    2. Sligar SG
    (1987) Metabolic switching in cytochrome P-450cam: deuterium isotope effects on regiospecificity and the monooxygenase/oxidase ratio. J Am Chem Soc 109:3754–3760.
    OpenUrlCrossRef
  2. ↵
    1. de Groot MJ,
    2. Ackland MJ,
    3. Horne VA,
    4. Alex AA,
    5. Jones BC
    (1999) A novel approach to predicting P450-mediated drug metabolism. CYP2D6 catalyzed N-dealkylation reactions and qualitative metabolite predictions using a combined protein and pharmacophore model for CYP2D6. J Med Chem 42:4062–4070.
    OpenUrlCrossRefPubMed
  3. ↵
    1. de Groot MJ,
    2. Denkelder GMDO,
    3. Commandeur JNM,
    4. Vanlenthe JH,
    5. Vermeulen NPE
    (1995) Metabolite predictions for parasubstituted anisoles based on Ab-Initio complete active space self-consistent-field calculations. Chem Res Toxicol 8:437–443.
    OpenUrlCrossRefPubMed
  4. ↵
    1. Dewar MJS,
    2. Zoebisch EG,
    3. Healy EF,
    4. Stewart JJP
    (1985) AM1: a new general purpose quantum mechanical molecular model. J Am Chem Soc 107:3902–3909.
    OpenUrlCrossRef
  5. ↵
    1. Fisher MB,
    2. Zheng YM,
    3. Rettie AE
    (1998) Positional specificity of rabbit CYP4B1 for omega-hydroxylation 1 of short-medium chain fatty acids and hydrocarbons. Biochem Biophys Res Commun 248:352–355.
    OpenUrlCrossRefPubMed
  6. ↵
    1. Grogan J,
    2. DeVito SC,
    3. Pearlman RS,
    4. Korzekwa KR
    (1992) Modeling cyanide release from nitriles: prediction of cytochrome P450-mediated acute nitrile toxicity. Chem Res Toxicol 5:548–552.
    OpenUrlCrossRefPubMed
  7. ↵
    1. Hanzlik RP,
    2. Hogberg K,
    3. Judson CM
    (1984) Microsomal hydroxylation of specifically deuterated monosubstituted benzenes. Evidence for direct aromatic hydroxylation. Biochemistry 23:3048–3055.
    OpenUrlCrossRefPubMed
  8. ↵
    1. Hanzlik RP,
    2. Ling K-HJ
    (1990) Active site dynamics of toluene hydroxylation by cytochrome P450. J Org Chem 55:3392–3397.
    OpenUrl
  9. ↵
    1. Harris JW,
    2. Jones JP,
    3. Martin JL,
    4. LaRosa AC,
    5. Olson MJ,
    6. Pohl LR,
    7. Anders MW
    (1992) Pentahaloethane-based chlorofluorocarbon substitutes and halothane: of in vivo hepatic protein-trifluoroacetylation and urinary trifluoroacetic acid excretion with calculated enthalpies of activation. Chem Res Toxicol 5:720–725.
    OpenUrlCrossRefPubMed
  10. ↵
    1. Higgins L,
    2. Bennett GA,
    3. Shimoji M,
    4. Jones JP
    (1998) Evaluation of cytochrome P450 mechanism and kinetics using kinetic deuterium isotope effects. Biochemistry 37:7039–7046.
    OpenUrlCrossRefPubMed
  11. ↵
    1. Higgins L,
    2. Korzekwa KR,
    3. Rao S,
    4. Shou M,
    5. Jones JP
    (2001) An assessment of the reaction energetics for cytochrome P450-mediated reactions. Arch Biochem Biophys 385:220–230.
    OpenUrlCrossRefPubMed
  12. ↵
    1. Hjelmeland LM,
    2. Aronow L,
    3. Trudell JR
    (1977a) Intramolecular determination of primary kinetic isotope effects in hydroxylations catalyzed by cytochrome P-450. Biochem Biophys Res Commun 76:541–549.
    OpenUrlCrossRef
  13. ↵
    1. Hjelmeland LM,
    2. Aronow L,
    3. Trudell JR
    (1977b) Intramolecular determination of substituent effects in hydroxylations catalyzed by cytochrome P-450. Mol Pharmacol 13:634–639.
    OpenUrlAbstract/FREE Full Text
  14. ↵
    1. Iyer KR,
    2. Jones JP,
    3. Darbyshire JF,
    4. Trager WF
    (1997) Intramolecular isotope effects for benzylic hydroxylation of isomeric xylenes and 4,4′-dimethylbiphenyl by cytochrome P450—relationship between distance of methyl groups and masking of the intrinsic isotope effect. Biochemistry 36:7136–7143.
    OpenUrlCrossRefPubMed
  15. ↵
    1. Jones JP,
    2. Korzekwa KR,
    3. Rettie AE,
    4. Trager WF
    (1986) Isotopically sensitive branching and its effect on the observed intramolecular isotope effects in cytochrome P450-catalyzed reactions: a new method for the estimation of intrinsic isotope effects. J Am Chem Soc 108:7074–7078.
    OpenUrlCrossRef
  16. ↵
    1. Jones JP,
    2. Rettie AE,
    3. Trager WF
    (1990) Intrinsic isotope effect suggest that the reaction coordinate symmetry for the P-450-catalyzed hydroxylation of octane is isozyme independent. J Med Chem 33:1242–1246.
    OpenUrlCrossRefPubMed
  17. ↵
    1. Karki S,
    2. Dinnocenzo JP,
    3. Jones JP,
    4. Korzekwa KR
    (1995) Mechanism of oxidative amine dealkylation of substituted N,N-dimethylanilines by cytochrome P-450—application of isotope effect profiles. J Am Chem Soc 117:3657–3664.
    OpenUrlCrossRef
  18. ↵
    1. Korzekwa KR,
    2. Jones JP,
    3. Gillette JR
    (1990a) Theoretical studies on cytochrome P-450-mediated hydroxylation: a predictive model for hydrogen atom abstractions. J Am Chem Soc 112:7042–7046.
    OpenUrlCrossRef
  19. ↵
    1. Korzekwa KR,
    2. Swinney DC,
    3. Trager WF
    (1989) Isotopically labeled chlorobenzenes as probes for the mechanism of cytochrome P-450 catalyzed aromatic hydroxylation. Biochemistry 28:9019–9027.
    OpenUrlCrossRefPubMed
  20. ↵
    1. Korzekwa KR,
    2. Trager WF,
    3. Nagata K,
    4. Parkinson A,
    5. Gillette JR
    (1990b) Isotope effect studies on the mechanism of the cytochrome P-450IIA1-catalyzed formation of Δ6-testosterone from testosterone. Drug Metab Dispos 18:974–979.
    OpenUrlAbstract
  21. ↵
    1. Lightfoot T,
    2. Ellis SW,
    3. Mahling J,
    4. Ackland MJ,
    5. Blaney FE,
    6. Bijloo GJ,
    7. de Groot MJ,
    8. Vermeulen NP,
    9. Blackburn GM,
    10. Lennard MS,
    11. Tucker GT
    (2000) Regioselective hydroxylation of debrisoquine by cytochrome P4502D6: implications for active site modelling. Xenobiotica 30:219–233.
    OpenUrlCrossRefPubMed
  22. ↵
    Lindsay-Smith JR and Sleath PR (1983) Model systems for cytochrome P450 dependent mono-oxygenases. Part 2. Kinetic isotope effects for the oxidative demethylation of anisole and [Me-2H3]anisole by cytochrome P450 dependent mono-oxygenases and model systems.J Chem Soc Perkin Trans 2 621–628..
  23. ↵
    1. Morohashi K,
    2. Sadano H,
    3. Okada Y,
    4. Omura T
    (1983) Position specificity in n-hexane hydroxylation by two forms of cytochrome P-450 in rat liver microsomes. J Biochem (Tokyo) 93:413–419.
    OpenUrlAbstract/FREE Full Text
  24. ↵
    1. Rao S,
    2. R. Aoyama M,
    3. Schrag WF,
    4. Trager A,
    5. Rettie,
    6. Jones JP
    (2000) A refined 3-dimensional QSAR of cytochrome P450 2C9: computational predictions of drug interactions. J Med Chem 43:2789–2796.
    OpenUrlCrossRefPubMed
  25. ↵
    1. Szklarz GD,
    2. Graham SE,
    3. Paulsen MD
    (2000) Molecular modeling of mammalian cytochromes P450: application to study enzyme function. Vitam Horm Adv Res Appl 58:53–87.
  26. ↵
    1. Szklarz GD,
    2. Halpert JR
    (1997) Use of homology modeling in conjunction with site-directed mutagenesis for analysis of structure-function relationships of mammalian cytochromes P450. Life Sci 61:2507–2520.
    OpenUrlCrossRefPubMed
  27. ↵
    1. Tassaneeyakul W,
    2. Birkett DJ,
    3. Edwards JW,
    4. Veronese ME,
    5. Tukey RH,
    6. Miners JO
    (1996) Human cytochrome P450 isoform specificity in the regioselective metabolism of toluene and o-, m-, and p-xylene. J Pharmacol Exp Ther 276:101–108.
    OpenUrlAbstract/FREE Full Text
  28. ↵
    1. White RE,
    2. McCarthy M,
    3. Egeberg KD,
    4. Sligar SG
    (1984) Regioselectivity in the cytochromes P450: control by protein constraints and chemical reactivities. Arch Biochem Biophys 228:493–502.
    OpenUrlCrossRefPubMed
  29. ↵
    1. White RE,
    2. Miller JP,
    3. Favreau LV,
    4. Bhattachararyya A
    (1986) Stereochemical dynamics of aliphatic hydroxylation by cytochrome P-450. J Am Chem Soc 108:6024–6031.
    OpenUrlCrossRef
  30. ↵
    1. Xue LL,
    2. Wang HF,
    3. Wang QM,
    4. Szklarz GD,
    5. Domanski TL,
    6. Halpert JR,
    7. Correia MA
    (2001) Influence of P450 3A4 SRS-2 residues on cooperativity and/or regioselectivity of aflatoxin B-1 oxidation. Chem Res Toxicol 14:483–491.
    OpenUrlCrossRefPubMed
  31. ↵
    1. Yin H,
    2. Anders MW,
    3. Korzekwa KR,
    4. Higgins L,
    5. Thummel KE,
    6. Kharasch ED,
    7. Jones JP
    (1995) Designing safer chemicals: predicting the rates of metabolism of halogenated alkanes. Proc Nat Acad Sci USA 92:11076–11080.
    OpenUrlAbstract/FREE Full Text
Back to top

In this issue

Download PDF
Article Alerts
Email Article
Citation Tools

Research ArticleArticle

Computational Models for Cytochrome P450: A Predictive Electronic Model for Aromatic Oxidation and Hydrogen Atom Abstraction

Jeffrey P. Jones, Michael Mysinger and Kenneth Ray Korzekwa
Drug Metabolism and Disposition January 1, 2002, 30 (1) 7-12; DOI: https://doi.org/10.1124/dmd.30.1.7
Twitter logo Facebook logo Mendeley logo

Jump to section

Advertisement