Abstract
Studies on the Caco-2 cell monolayer system that contained cytochrome P450 and P-glycoprotein activities had advanced the theory that increased intestinal metabolism resulted with increased drug efflux due to an increase in mean residence time (MRT) in the system. To confirm or refute the claim, we developed compartmental models to study the effects of intestinal secretion on the MRT and rates of metabolism under first-order and nonlinear conditions. The theoretical examinations showed that under first-order conditions, intestinal secretion increased the MRT of drug in all compartments but failed to increase the rate of metabolite formation or the total amount of metabolite formed. Instead, reduced metabolic rates arose with increased efflux from cell, either into the apical or the basolateral compartment. By contrast, under saturable metabolic conditions, there were some conditions found whereby rates of metabolism increased with intestinal secretion and rapid reabsorption, albeit the total amount of metabolite formed eventually equaled the administered dose. Intestinal secretion failed to induce higher rates of metabolism for other conditions (saturable cellular binding, cellular efflux, or cell entry). With saturation of metabolic enzymes, drug efflux brought about desaturation, and, upon rapid recovery of drug into the cellular compartment, higher rates of metabolite formation were attained. The simulation study showed that, under first-order conditions, intestinal secretion reduced the rate of metabolism even though the MRT was prolonged within the cell preparation. With nonlinear metabolism, however, instances may exist whereby higher rates of metabolism would result with secretion.
The intestine is the first physical barrier to which drug is presented following oral administration. In addition to transporters for uptake (Tsuji and Tamai, 1996), drug-metabolizing enzymes for oxidation and conjugation (Dubey and Singh, 1988; Ilett et al., 1990) and efflux transporters for excretion are present (Lin et al., 1999; Suzuki and Sugiyama, 2000). An important efflux transporter is P-glycoprotein (Pgp1), a multidrug resistance (MDR1) gene product that is present at the villous tips of the enterocytes (Thiebaut et al., 1987). Drugs that are substrates of Pgp include verapamil (Saitoh and Aungst, 1995; Sandström et al., 1998; Johnson et al., 2001); the anticancer drugs vincristine, etoposide, daunorubicin, and paclitaxel (Leu and Huang, 1995; Sonnichsen et al., 1995; Nakayama et al., 2000; Chico et al., 2001; Wacher et al., 2001; Abraham et al., 2002); digoxin (Cavet et al., 1996; Greiner et al., 1999); the human immunodeficiency virus protease inhibitor indinavir (Hochman et al., 2000; Li et al., 2002); and immunosuppressive agents cyclosporin (Gan et al., 1996; Lown et al., 1997), tacrolimus (Lampen et al., 1996; Hashimoto et al., 1998; Hashida et al., 2001), and sirolimus (Paine et al., 2002).
Because of the significance of the intestine as an important first-pass organ, in vitro systems have been developed to assess the importance of intestinal uptake, metabolism, and excretion for the prediction of permeability and overall absorption. Among these are intestinal membrane segments/preparations (Johnson et al., 2001), everted sacs (Carreno-Gomez and Duncan, 2000), and the Ussing chamber (Fiddian-Green and Silen, 1975). In these systems, a donor compartment for drug administration and a receiving compartment for sampling allow the estimation of drug absorption, metabolism, and efflux. Mucosal administration allows investigation of drug flux in the mucosal to serosal direction, whereas drug given at the serosal side permits the flux in the opposite direction, that is, from the serosal (basolateral) to mucosal compartment to be estimated. Another system is the cultured Caco-2 cell monolayer derived from human colon carcinoma cells. When differentiated Caco-2 cells were employed to study drug efflux by Pgp (Saitoh and Aungst, 1995), the involvement of Pgp was inferred when the basolateral to apical flux (B to A) exceeded that of A to B. It was further found that, upon culture in 1α-25-dihydroxy vitamin D3 for 2 weeks postconfluence, cytochrome P450 3A activity was up-regulated (Schmiedlin-Ren et al., 1997; Thummel et al., 2001). More recently, transfection with the cytochrome P450 gene and stimulation by butyrate (Cummins et al., 2001) were employed to express the P450 activity.
Recent studies on the interactions between the cytochromes P450 and Pgp in intestinal removal within in vitro preparations have led to the conclusion that intestinal metabolism is enhanced by the secretory action of Pgp because of an increase in the mean residence time for drug (MRT) in the intestine (Johnson et al., 2001; 2003; Cummins et al., 2002). Although there have been several theoretical investigations on metabolism and secretion occurring concurrently in the intestine (Yu and Amidon, 1998; Ito et al., 1999; Cong et al., 2000), few have thoroughly addressed the effect of secretion on metabolism in the in vitro systems. But reports existed on metabolism and secretion occurring concurrently within an eliminating organ that secretion decreased the rates of metabolism due to the depletion of the intracellular substrate concentration (Sirianni and Pang, 1997; Schuetz and Schinkel, 1999). Hence, we tested the hypothesis that under linear conditions, secretion by Pgp in these in vitro systems decreased the rate of metabolism because of removal of substrate, despite the fact that the mean residence time was increased. We further examined other circumstances whereby secretion might increase the rate of metabolism in these in vitro systems.
Materials and Methods
Models and Solutions. The schematic depictions of the Caco-2 cell monolayer and membrane preparation are similar, and are shown in Fig. 1. It was assumed that drug metabolism is confined to the cellular monolayer and is described by the first-order, metabolic intrinsic clearance, CLint,met (Scheme A), or by a saturable system characterized by the Michaelis-Menten constant, Km, and the maximum velocity, Vmax (Scheme B). In Scheme B, nonlinear conditions for absorption, efflux, or cellular binding were readily accommodated. The mass balance equations for the apical (denoted by subscript, ap), cell (denoted by subscript, cell) and the basolateral (denoted by subscript, baso) compartments are shown in the Appendix.
Schematic presentation of the simpler Caco-2 cell system that consists of a donor, an apical compartment, a cell monolayer compartment, and a receiving compartment, the basolateral compartment (Scheme A, linear case); and the extended model (Scheme B, nonlinear case) that further considers nonlinear metabolism from the cellular compartment (with Vmaxand Km).
Only the unbound drug traverses across the compartments. See text for details.
Scheme A: Linear conditions. Permeation of drug (D) from the apical compartment into the cell layer, whether mediated by uptake transporters or passive diffusion, is associated with the absorption rate constant, ka, whereas secretion from the cell back into the apical compartment occurs with the intrinsic clearance, CLint,sec. Drug partitioning between the cell and the basolateral compartment is mediated by influx and efflux clearances, CLd1 and CLd2, respectively, as shown. Drug binding to proteins present in the apical compartment due to sloughed off mucosal cells (unbound fraction fap), within the cell (unbound fraction fcell), and in the basolateral compartment (unbound fraction fbaso) affects the transfer and metabolic rates based on unbound drug concentrations. Metabolite formation is assumed to occur from the cellular compartment. At any time, the rate of total metabolite formed under first-order conditions is given by fcellDcellCLint,met/Vcell, where Dcell is the amount of drug within the cellular compartment of volume, Vcell. Estimation of metabolite formation under first-order conditions was simplified by setting the efflux clearances of metabolite from the cellular compartment as zero. The total amount of metabolite formed within the cellular compartment may be obtained by integration of the metabolite formation rates with respect to time, and this amount was further normalized to the dose.
Under first order conditions, the area under the curve for drug (AUC) and area under the moment curve for drug (AUMC) were solved by inversion of the square matrix (shown in the Appendix for Scheme A) with the program, Theorist, as described previously (Pang, 1995). The MRT for the drug for first-order conditions was obtained as the ratio of AUMC/AUC (Eq. 1). The MRTcell within the cell or AUMCcell/AUCcell provides a pertinent parameter of the duration of drug in the eliminating tissue. 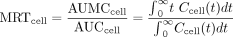
Scheme B: Nonlinear metabolism. Scheme B further considers nonlinear drug metabolism (characterized by Vmax and Km) to form the metabolite, M (Fig. 1B), and nonlinearity in absorption, cellular efflux, or tissue binding. The formed metabolite may, in some instances, affect the transport processes or the binding of drug and, in turn, the rate of drug metabolism. Binding of metabolite is assumed to be unity, and transport processes of the metabolite may be described in Scheme B since the formed metabolite may be an inhibitor or inducer for drug transport or metabolism, and these may be modeled, in future studies. Metabolite within the cell (Mcell) may be effluxed out with clearances, CLint,sec{mi} and CLd2{mi}, respectively, into the apical and basolateral compartments. The metabolite from the apical compartment (Map) is transported into the cell monolayer with the rate constant, ka{mi}, whereas that (Mbaso) from the basolateral compartment is transported into the cell monolayer with the transfer clearance, CLd1{mi}. The AUC and AUMC for the simulated drug data (up to 5,000 min) were obtained by the trapezoidal rule, with extrapolation to infinity. The MRTcell under nonlinear conditions was given by eq. 2 (Rescigno, 1973; Cheng and Jusko, 1989) and was based on the instantaneous metabolic intrinsic clearance, CLint,met(t) at time t shown in eq. 3. 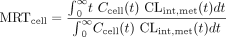

The total amount of metabolite formed was provided by the sum of the amounts of metabolite in all compartments.
Simulations. Data were simulated for apical (denoted by subscript, A) and basolateral (denoted by subscript, B) dosings. Recovery of the dose was tested and was complete in all simulations. Values of Vap (1.5 ml) and Vbaso (2.5 ml) were based on the data of Cummins et al. (2002). The value of Vcell (0.1 ml) was arbitrarily chosen, since the volume of the cell layer was unimportant for both linear and nonlinear simulations (data not shown).
Linear cases. The circumstances for simulations of the first-order conditions are summarized in Table 1 (Scheme A). An initial drug concentration of 1 μM was used. The solutions (shown in Table 2) were used to estimate the AUC, AUMC, and MRT with apical (mucosal) or basolateral administration with the assigned values of Vap, Vbaso, and Vcell. Values of ka, ka{mi}, fap, fcell, fcell, CLd1, CLd2, CLint,sec, CLd1{mi}, CLd2{mi}, and CLint,sec{mi} were assumed to be independent of concentration and time for simulations of the linear cases. Initially, values of the intrinsic clearances and the absorption constants were varied to provide suitable profiles, and these served as the basis for simulations (Table 1). The intrinsic clearance for secretion (CLint,sec) was varied from 0 to 10 ml/min whereas the intrinsic clearance for metabolism (CLint,met) was varied from 0 to 1 ml/min for cases 1 to 4. The value of ka was set as 0.01 min-1 since this provided a reasonable time course for transport and metabolism (see later simulations). CLd1 and CLd2 values of 50, 5, 0.5 or 0.01 ml/min, spanning for cases of high permeability (50 ml/min) to low permeability (0.01 ml/min), and unbound fractions of unity for fap, fcell, and fbaso, were used (Cases 1–4, Table 1).
Simulations performed for Scheme A
Cases 5 to 13 were used for simulation of the time course of metabolite formation.
Solutions to Scheme A
The time courses of metabolite formation (Cases 5–13 for Scheme A, Table 1) were derived using the program, Scientist (Micromath, Utah), with rate equations shown in the Appendix. Only one parameter was being varied at a time (Table 1). The set of parameters was chosen since changes for metabolite formation were obtained within 3 h. The metabolic intrinsic clearance CLint,met was assigned the value of 1 ml/min when all the diffusional clearances (CLd1 and CLd2) were held constant as 50 ml/min; the secretory clearance, CLint,sec, was set as 5 ml/min. The absorption rate constant ka was assigned the value, 0.01 min-1. The unbound fractions, fap, fcell, and fbaso were constant at 1.0.
Nonlinear cases. In the second set of simulations, saturable metabolism/absorption/binding/efflux was included (Scheme B, Fig. 1). The chosen values for the metabolite: ka{mi} = 0.05 min-1, CLd1{mi} = 0.05 ml/min, CLd2{mi} = 0.1 ml/min, CLint,sec{mi} = 1 ml/min, for simulation were inconsequential in the present simulation since it was assumed that the metabolite failed to alter the kinetics of drug.
As for the saturable metabolism, the Vmax (10 to 50 nmol/min) and Km (10 to 50 μM) were varied for the metabolic pathway. Initial drug concentrations of 100 and 300 μM were used, and simulations were performed with fap = fcell = fbaso = 1. CLd1 and CLd2 were varied from 0.02, to 0.5, 1, and 5 ml/min, spanning from low to high transmembrane permeability. Values of ka (1 and 30 min-1) and CLint,sec (1, 5, and 10 ml/min) were used.
Saturable absorption (ka pathway) was examined when the metabolic intrinsic clearance was linear and constant (first-order; CLint,met = 0.5 ml/min). CLd1 and CLd2 were assigned the value of 5 ml/min such that drug partitioning was rapid and not an issue. Various Vmax (10 and 50 nmole/min) and Km (10, 20, and 50 μM) were used to describe saturable absorption at 100 and 1000 μM, when CLint,sec was varied from 1 to 5 and 10 ml/min.
For study of nonlinear protein binding, the following equation, derived from the binding isotherm, was used to relate the unbound cellular concentration of drug, Ccell,u, to the total cellular concentration, Ccell, since the unbound drug in cell traverses the membranes and is the species that is metabolized. 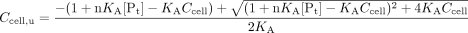 The binding association constant (KA) was varied from 104 to 106 and 108 M-1, and the classes and number of binding sites were set as unity. The cellular protein concentration [Pt] was assumed to be 4,000 μM (assuming 16 g of cytosolic protein/100 ml of intracellular fluid and an average molecular weight of 40,000 for the cytosolic proteins). The absorption rate constant (ka) was varied from 1 to 30 min-1, and CLd1 and CLd2 were varied from 0.05 to 5 ml/min; the metabolic intrinsic clearance, CLint,met, was kept constant at 0.5 ml/min. The input concentration was varied from 100 to 5,000 μM.
The binding association constant (KA) was varied from 104 to 106 and 108 M-1, and the classes and number of binding sites were set as unity. The cellular protein concentration [Pt] was assumed to be 4,000 μM (assuming 16 g of cytosolic protein/100 ml of intracellular fluid and an average molecular weight of 40,000 for the cytosolic proteins). The absorption rate constant (ka) was varied from 1 to 30 min-1, and CLd1 and CLd2 were varied from 0.05 to 5 ml/min; the metabolic intrinsic clearance, CLint,met, was kept constant at 0.5 ml/min. The input concentration was varied from 100 to 5,000 μM.
Results
Scheme A: Linear Conditions.Effect of CLints and tissue partitioning on AUC and MRT. The simpler model (Scheme A) revealed that the solution for AUC in both the apical and basolateral compartments (AUCap and AUCbaso) differed according to the site of drug application (Table 2). All of the AUCs were inversely related to the unbound fraction for the compartment and were route-dependent except for AUCcell, which remained identical for apical and basolateral administrations. AUCcell was independent of CLint,sec and was equal to the quotient of the dose and the metabolic intrinsic clearance, CLint,met, multiplied to the unbound fraction in cell. The total metabolite formation (CLint,metfcell AUCcell = Metcell) was independent of secretion and equaled the administered dose when time reached infinity. The ratio of AUCap,A/AUCbaso,A after apical dosing was (CLint,met + CLint,sec)CLd1fbaso/(CLd2Vapfapka), and that of AUCbaso,B/AUCap,B after basolateral dosing was (CLd2 + CLint,met)Vapfapka/(CLd1CLint,secfbaso). It could readily be deciphered that the metabolic and secretory intrinsic clearances, the transfer or partitioning clearances, the volumes, the unbound fractions, and the absorption rate constant all influence these ratios.
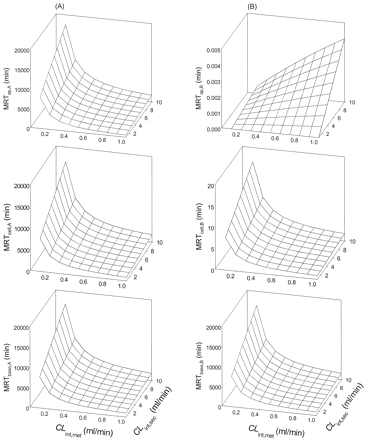
The MRTs in the apical, cell, and basolateral compartments were all increased with CLint,sec, since the term was present in the numerators of the solutions (Table 2). At high CLd1 and CLd2 (5 or 50 ml/min, Cases 1 and 2, Table 1), an increase in CLint,sec alone increased the MRTap, MRTcell, and MRTbaso and prolonged the mean residence times of substrate in all compartments. The trends were similar for both apical and basolateral administrations, reflecting the absence of a permeation barrier for cases 1 and 2 (Fig. 2). Reducing CLd1 (value reduced to 0.01 ml/min at CLd2 of 5 ml/min; Case 3, Table 1) failed to alter the CLint,sec-induced changes of the MRTs among the apical, cell, and basolateral compartments after apical dosing and for the basolateral compartment after dosing into that compartment, MRTbaso,B. In all cases, the MRTs increased with increasing CLint,sec (Fig. 3); the trends persisted even when CLd2 was reduced from 5 to 0.5 ml/min, at CLd1 = 0.01 ml/min (data not shown). A reduction of CLd2 only (value reduced to 0.01 ml/min at CLd1 of 5 ml/min; Case 4, Table 1) failed to perturb the trends for the MRTs in apical, cell, and basolateral compartments following apical administration. But distinct patterns were observed, especially for MRTap,B following basolateral dosing. The MRTcell,B, MRTap,B and MRTbaso,B arising from basolateral dosing were considerably lower than comparable ones after apical administration (Fig. 4). These scenarios persisted when CLd2 was reduced from 5 to 0.5 ml/min.
Simulations of MRTs for apical (A) and basolateral (B) administrations for Cases 1 and 2,Table 1(Scheme A).
The patterns of the MRTs were similar for both routes of drug administration, since CLd1 and CLd2 were high.
Simulations of MRTs for apical (A) and basolateral (B) administrations for Case 3,Table 1(Scheme A).
A transmembrane barrier existed, being more severe for transport from the basolateral compartment into the cellular compartment. The patterns of the MRTs were different for both routes of drug administration.
Simulations of MRTs for apical (A) and basolateral (B) administrations for Case 4,Table 1(Scheme A).
A transmembrane barrier existed, being more severe for transport from the cellular compartment into the basolateral compartment. The patterns of the MRTs were different for both routes of drug administration.
The above simulations (Figs. 2, 3, 4) showed that the permeation barrier was absent at 5 ml/min, whereas at lower CLd1 and CLd2, the transmembrane barriers started to affect the MRTs for both routes of administration. Nevertheless, the trend of increasing values of the MRT with increasing CLint,sec persisted for cases 1 to 4.
Effect of ka. The effects of ka on the AUC and the MRT are shown in Table 2. AUCap bore an inverse relationship with ka, regardless of the route of drug dosing. Moreover, ka bore an inverse relationship with all of the MRTs. With increasing ka, all of the MRTs decreased for all values of CLint,met (data not shown). Increasing the ka reduced the MRTs within the compartments and this persisted at different values of CLd1 and CLd2 (data not shown).
Factors affecting time course of metabolite formation. Although the AUCcell and the total amount of metabolite formed ultimately equaled the dose for both apical and basolateral dosing, the rate of accrual of metabolite was dependent on the incubation time. The time courses differed for the various cases. Metabolite accrual was strongly affected by ka, CLint,sec, CLint,met, CLd1, CLd2, the unbound fractions, and the route of administration. Increasing the ka, CLd1, or CLint,met increased the rate of metabolite accrual for both apical and basolateral administrations (Fig. 5). By contrast, increasing the CLint,sec or CLd2 (right panel) decreased the accrual rate of metabolite. At infinite time, the entire dose would ultimately be all metabolized.
Simulations of the rate of metabolite accrual with apical administration (Metcell,A) for Cases 5 to 9,Table 1(Scheme A) with increasing values of ka, CLd1, and CLint,met.
These resulted in increased rates of metabolite produced (left panel). By contrast, upon increasing the values of CLint,sec and CLd2 (right panel), the rates of metabolite produced decreased. The same patterns were observed for Metcell,B after basolateral administration.
Effect of binding on the time courses of metabolite formation. To investigate the effects of protein binding on the time course of the drug concentrations in the apical (Cap), cell (Ccell) and basolateral (Cbaso) compartments, high values (50 ml/min) were chosen for CLd1 and CLd2 to eliminate any barrier effect on drug permeation at the basolateral membrane. Binding and changes in binding in the apical, cellular, and basolateral compartments failed to alter the concentration-time profiles of substrate in the cell compartment (data not shown) for both routes of dosing, although the concentration-time courses of Cap and Cbaso and metabolite formation were affected by the unbound fractions fap (Fig. 6) and fbaso (Fig. 7). Binding also reduced the rates of metabolite accrual with either apical or basolateral administration (Figs. 6 and 7, lower panels). Similar effects of fbaso on metabolite formation were observed for midazolam metabolism in the Caco-2 system (Fisher et al., 1999).
Simulations of the changes in fap(0.01 and 1) on the concentrations of drug in the apical (Cap) and basolateral (Cbaso) compartments (left panel) and the accrual of metabolite formed following apical (Metcell,A) and basolateral (Metcell,B) dosing (right panel) for Scheme A.
Simulations of the changes in fbaso(0.01 and 1) on the concentrations of drug in the apical (Cap) and basolateral (Cbaso) compartments (left panel) and the accrual of metabolite formed following apical (Metcell,A) and basolateral (Metcell,B) dosing (right panel) for Scheme A.
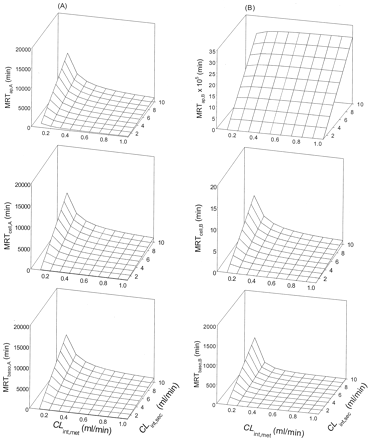
Scheme B: Nonlinear Cases. Values of Vmax and Km for metabolism, and values of ka, CLd1, and CLd2 were altered by trial and error to identify a condition whereby the rate of metabolite accrual and the MRTcell would increase upon increasing the CLint,sec. It was observed that increasing the Km (compare Tables 3, 4, 5) and decreasing the Vmax (compare Tables 5 and 6) for metabolism decreased the MRTcell at given values of ka (1 and 30 min-1) and designated transmembrane clearances of drug (CLd1 and CLd2 at 0.02–5 ml/min). Increasing the absorption rate constant, ka (cf. values at 1 and 30 min-1) and the permeability (CLd1 and CLd2) reduced the MRTcell (compare Tables 3, 4, 5, 6). Increasing the applied concentration to the apical or basolateral compartment usually prolonged MRTcell due to a greater saturation of the metabolic enzymes, thereby prolonging the residence of drug within the cell. Generally, increasing the CLint,sec brought about a prolongation in the MRTcell,A with drug administration into the apical compartment, except some cases of low CLd1 and CLd2 (0.02 and 0.5 ml/min, starred examples; Tables 3, 4, 5, 6). For basolateral application, however, a prolongation in the MRTcell,B occurred with increasing CLint,sec (Tables 3 and 6).
Scheme B: MRTcell as functions of CLint,sec, CLd1 CLd2, ka, and nonlinear metabolism (Km of 10 μM and Vmax of 10 nmol/min). Initial drug concentrations of 100 and 300 μM were used; eq. 2 was used to estimate the MRT.
Scheme B: MRTcell as functions of CLint,sec, CLd1, CLd2, ka, and nonlinear metabolism (Km of 20 μM and Vmax of 10 nmol/min). Initial drug concentrations of 100 and 300 μM were used; eq. 2 was used to estimate the MRT.
Scheme B: MRTcell as functions of CLint,sec, CLd1, CLd2, ka, and nonlinear metabolism (Km of 50 μM and Vmax of 10 nmol/min). Initial drug concentrations of 100 and 300 μM were used; eq. 2 was used to estimate the MRT.
Scheme B: MRTcell as functions of CLint,sec, CLd1, CLd2, ka, and nonlinear metabolism (Km of 50 μM and Vmax of 50 nmol/min). Initial drug concentrations of 100 and 300 μM were used; eq. 2 was used to estimate the MRT.
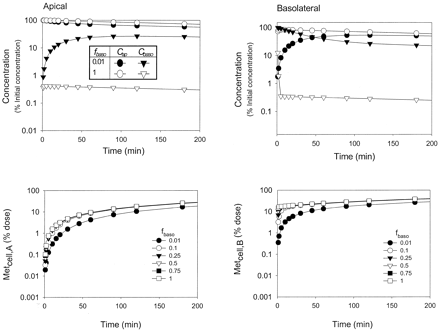
Under conditions of saturable metabolism, the rates of metabolite formation (Met) were increased with increasing secretion for several simulated cases where the drug permeability was low. Upon apical administration and rapid absorption (high ka of 30 min-1) at Km of 50 μM and Vmax of 10 nmol/min, increasing secretion resulted in increased rates of metabolism (Figs. 8C and 9C). The pattern occurred at both 100 μM (Fig. 8) and 300 μM (Fig. 9). At the higher Vmax (50 nmol/min), metabolite accrual rates were faster. This trend of increased rates of cellular metabolism with increased secretion persisted at the ka of 30 min-1 and low drug permeability (data not shown). Under saturable conditions for apical absorption, cellular efflux (CLd2 pathway), or cellular binding, however, metabolite accrual failed to increase with secretion (data not shown).
Scheme B: nonlinear metabolism and metabolite accrual at ka = 1 min-1 [(A) and (B)[or at ka = 30 min-1 [(C) and (D)] for the initial concentration of 100 μM.
Simulations were conducted for Vmax = 10 nmol/min and Km = 50 μM, when drug permeability was low (CLd1 = CLd2 = 0.02 ml/min) [(A) and (C)] or when drug permeability was high (CLd1 = CLd2 = 5 ml/min) [(B) and (D)]. The CLint,sec was varied from 1 (▪, □) to 5 (▾, ▿) and 10 (▴, ▵) ml/min; solid symbols are associated with apical administration and open symbols represent basolateral administration. Usually, increasing values of CLint,sec decreased the rates of metabolite accrual [see (A), (B), and (D)], except when reabsorption was rapid and permeability of drug was low [see (C)].
Scheme B: nonlinear metabolism and metabolite accrual at ka = 1 min-1 [(A) and (B)] or at ka = 30 min-1 [(C) and (D)] for the initial concentration of 300 μM.
Simulations were conducted for Vmax = 10 nmol/min and Km = 50 μM, when drug permeability was low (CLd1 = CLd2 = 0.02 ml/min) [(A) and (C)] or when drug permeability was high (CLd1 = CLd2 = 5 ml/min) [(B) and (D)]. The CLint,sec was varied from 1 (▪, □) to 5 (▾, ▿) and 10 (▴, ▵) ml/min; solid symbols are associated with apical administration and open symbols represent basolateral administration. Usually, increasing values of CLint,sec decreased the rates of metabolite accrual [see (A), (B), and (D)], except when reabsorption was rapid and permeability of drug was low [see (C)].
Discussion
The competing interactions of absorption, metabolism, and exsorption/efflux in the intestine have been the subject of recent investigations (Lin et al., 1999; Suzuki and Sugiyama, 2000; Wacher et al., 2001). The interplay is recognized to be of paramount importance in the determination of drug bioavailability since intestinal efflux is inferred to increase the mean residence time of drugs and to increase intestinal metabolism (Johnson et al., 2001, 2003; Cummins et al., 2002). The role of Pgp on intestinal drug metabolism has been much debated. The consideration is important since Caco-2 systems and similar techniques are the mainstay of high-throughput, in vitro systems, and perturbations are readily achieved with addition of putative inhibitors of Pgp or cytochrome P450 to the system. Lin et al. (1999) had questioned whether the role of Pgp was overemphasized. The role of Pgp is de-emphasized when saturation of the secretory pathway exists (Dr. Jiunn Lin, personal communication) and, as shown in this simulation study, when reabsorption (high ka) is facile in recovery of the drug. Several reports had asserted that increased intestinal metabolism was associated with the actions of Pgp, and the total amount of metabolite accumulated in all compartments increased with increased mean residence time (Johnson et al., 2001, 2003; Cummins et al., 2002). However, the above conjecture is against theory based on linear treatise and competition reactions (Sirianni and Pang, 1997).
From results of the present theoretical examination, the question of secretion increasing the MRT and metabolism has become clarified. Indeed, under first-order conditions, there is increase in the mean residence time of drug within all of the compartments. The outcome is not unexpected since the cycling between drug in the cell and apical compartments due to efflux and reabsorption presents a closed loop that is akin to the addition of a peripheral (apical) compartment to the open, cellular compartment. The consequence is an increase in the MRT for all compartments (apical, cell, and basolateral). But there are differences in the extents of the increase in MRTs, since the diffusional constants, CLd1 and CLd2, and ka play additional modulating roles. A faster absorption rate constant, ka, counteracts the depth of the virtual, peripheral compartment and reduces the MRT. However, in contrast to previous speculation, there was a lack of increase in metabolite formation with increasing CLint,sec. If sampling is conducted at infinite time, no apparent difference should be observed for total metabolism. Thus, in contrast to popular thinking, Pgp would not increase the ultimate production of metabolite.
Under first-order conditions, increased CLint,sec renders a slower time course of metabolite production since the substrate is being removed competitively at the site of metabolism by efflux (Fig. 5). It has been recognized that the mutual presence of competing pathways by the efflux transporter for secretion and intracellular enzymes for metabolism lowers the intracellular substrate concentration within the tissue site (Sirianni and Pang, 1997; Schuetz and Schinkel, 1999). This line of reasoning holds true even when cellular metabolism occurs within the cellular milieu and Pgp exists on the membrane or a separate, distinct compartment (simulations not shown). The same trend persisted with physiological modeling of the intestine in the form of the traditional, physiological model (TM) and the segregated flow model (SFM) presented earlier (Cong et al., 2000; Doherty and Pang, 2000). These models predicted reduced metabolism with intestinal secretion (D. Tam and K. S. Pang, unpublished data), and the same conclusions are drawn. Because metabolism decreases with increasing drug efflux and is time-dependent, additional questions may be asked on the rationale of the sampling times for the in vitro experiments.
The present investigation also explored the effects of nonlinear cellular binding, absorption, or metabolism, and whether increasing secretion could bring about increased rates of metabolite accrual. Since increased efflux would desaturate the enzymes, there were instances in which increasing secretion could bring about increased rates of intestinal metabolism, especially when rapid recovery into the cell existed. The extent of intestine metabolism in this in vitro system, however, remained unchanged and eventually equaled the dose. Nonlinear protein binding inside the cell showed lower free fractions at declining drug concentrations that ensued with time, and this would slow down drug metabolism. With nonlinear absorption, increased efflux to the apical compartment would saturate drug absorption into the cell, and under extreme conditions, absorption may even become zero-order, further reducing the intracellular drug concentration and slowing down drug metabolism.
Although our investigation was of limited scope, the findings revealed that increased secretion brought about increased metabolite accrual only with saturable metabolism, rapid apical absorption, and low drug partitioning at the basolateral compartment upon apical dosing (Figs. 8C and 9C). Secretion brought about desaturation of the enzymatic system. At high ka, the rapid reabsorption replenished the substrate for cellular metabolism that was occurring more optimally under desaturated conditions. The total amount of metabolite ultimately formed, however, remained equal to the dose. However, there was no apparent correlation between MRTcell and metabolite accrual (Tables 3, 4, 5, 6; Figs. 8 and 9).
To properly address the type of changes expected of Pgp and cytochrome P450 and the presence of the inhibitors (Johnson et al., 2003), the experimenter needs to be cognizant that many of the described variables are capable of affecting drug disappearance and metabolite accrual. A better approach, in our minds, is to describe the absorption and efflux as separate events instead of “net absorption” (Johnson et al., 2003), so as to segregate the effect of entry versus efflux and/or metabolism after the drug has gained entry into the cell. Under first-order conditions, increasing values of ka, CLd1, CLint,met, fap, and fbaso increased, whereas increasing values of CLint,sec and CLd2 decreased the rate of metabolite formation (Figs. 5, 6, 7). Alternately, when drug metabolism occurs under saturating conditions, there are instances where an increase in CLint,sec may evoke higher rates of metabolite accrual (Figs. 8C and 9C). The complete understanding of the interaction between drug partitioning, metabolic enzymes, and Pgp secretion lends to the better prediction of intestinal drug absorption and bioavailability.
Appendix
Scheme A: Linear case. The mass balance rate-equations for Scheme A (eqs. A1–A3) are presented below, where D and M are the amounts of drug and metabolite, respectively, and subscripts ap, cell, and baso denote the apical, cellular, and basolateral compartments, respectively. 

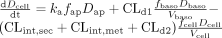
 The following square matrix resulted for Scheme A,
The following square matrix resulted for Scheme A, 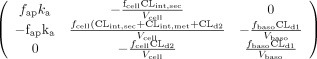
Scheme B: Nonlinear Case. The rate equations for the apical and basolateral compartments were identical to those for Scheme A (eqs. A1 and A2). However, the rate equation for drug in the cellular compartment differed.  Similarly, the rate equations for the rate of change of metabolite (M) in the apical, basolateral, and cellular compartments are shown below.
Similarly, the rate equations for the rate of change of metabolite (M) in the apical, basolateral, and cellular compartments are shown below. 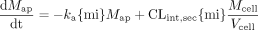
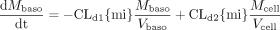
 The dose-corrected amount of metabolite formed at any time is given by the sum of the amounts of M in the compartments.
The dose-corrected amount of metabolite formed at any time is given by the sum of the amounts of M in the compartments. 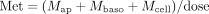
Footnotes
-
↵1 Abbreviations used are: Pgp, P-glycoprotein; AUC, area under the curve; MRT, mean residence time for drug; CLd1 and CLd2, CLd1{mi} and CLd2{mi}, transfer clearances from basolateral compartment to cell, and from cell to basolateral compartment, for drug and metabolite mi, respectively; CLint,met, metabolic intrinsic clearance for drug; CLint,sec and CLint,sec{mi}, secretory intrinsic clearances for drug and metabolite, respectively; fap, fcell, and fbaso, unbound fractions of drug in the apical, cell, and basolateral compartment, respectively; ka and ka{mi}, absorption rate constants for drug and metabolite, respectively; AUMC, area under the moment curve.
-
This work was supported by the Canadian Institute for Health Research, Grant MOP36457. D.T. was a recipient of a Natural Sciences and Engineering Research Council of Canada summer studentship.
- Received February 24, 2003.
- Accepted June 25, 2003.
- The American Society for Pharmacology and Experimental Therapeutics