A major focus of the pharmaceutical industry is early prediction of the likelihood and the magnitude of drug-drug interactions. DDIs involving CYP3A4 are particularly important, because mibefradil, terfenadine, astemizole, cisapride, and cerivastatin were all removed from the US market in recent years, at least in part, because of safety issues exacerbated by CYP3A4 DDIs. An understanding of the risk for DDIs associated with a new chemical entity is a key component of both the drug discovery and development processes. The earlier that risks for DDIs can be identified for new chemical entities under consideration as potential drugs, the greater the probability that this risk can be removed via drug design efforts.

For compounds already in clinical development, in vitro DDI projections can be used to prioritize and optimize the design of the appropriate clinical DDI studies. Evaluations of the impact of a new chemical entity (Palmer et al., 2001) on a specific enzyme pathway using probe substrates may be extrapolated to other drugs whose clearances occur via the same pathway and to situations in which several pathways may be affected simultaneously. Alternatively, new chemical entities may be evaluated for DDIs via interactions with drugs determined to have potential for comedication and, in this situation, effects on multiple pathways may need to be considered for study design optimization. Evaluations built using in vitro probe substrate data and simulated patient populations also enable the scientist to predict the range of magnitude of DDIs in individual subjects who may have reduced metabolic capacity.

Numerous researchers (Kanamitsu et al., 2000a; Blanchard et al., 2004; Ito et al., 2004; Brown et al., 2006; Galetin et al., 2008; Ohno et al., 2008) have used a variety of mathematical models that require static values of precipitant concentrations in the intestine and liver for the prediction of DDIs. However, at present, there is no consensus on the in vivo precipitant concentration that should be used. For instance, the unbound systemic concentration has been widely used for predicting DDIs caused by induction and time-dependent inhibition, whereas the estimated unbound portal concentration has been the preferred value for reversible inhibition.

One of the difficulties in conducting a DDI risk assessment is how to integrate data from in vitro interaction experiments, such as reversible inhibition studies, time-dependent inhibition studies, and induction studies, into an overarching evaluation of the impact of the coadministration of one compound with another. An example of this is the herbal agent St. John's wort, which was demonstrated to be a potent in vitro inhibitor of CYP3A4 (Obach, 2000). However, in vivo it was shown to be an inducer of CYP3A4, and this effect was also seen in in vitro induction studies (Moore et al., 2000). Projecting potential clinical DDIs from in vitro data has progressed from specific endpoint analysis based on the relationship between the projected therapeutic concentration of the drug and its reversible binding affinity for the particular enzyme of interest (I/K_i) (Kanamitsu et al., 2000a; Tucker et al., 2001; Blanchard et al., 2004; Bachmann and Lewis, 2005) to a comprehensive analysis including the simultaneous evaluation of the potential impact of reversible inhibition, time-dependent inhibition, and induction (Fahmi et al., 2008b).

The idea of a mathematical model for drug-drug interactions, developed from in vitro data, offers a quantitative approach to improving decision making in drug development and discovery. With the Simcyp approach, the combined knowledge of in vitro DDI data and clinical pharmacokinetics of the drug can be used to simulate various clinical DDI trial scenarios (Einolf, 2007; Jamei et al., 2009) to identify an efficient and effective clinical DDI study strategy. This approach eliminates the need for numerous unnecessary clinical DDI studies and accelerates the availability of therapy to patients.

In this study, we compared two models for predicting DDIs. We used a mathematical model that simultaneously incorporates reversible inhibition and time-dependent inhibition, and induction for both have an impact on the liver and intestines for a CYP3A4-based DDI. In addition, we used the mechanistic dynamic model from a population-based absorption, distribution, metabolism, and excretion simulator (Simcyp).

Materials and Methods

Data Source. Clinical midazolam DDI data were collected from the University of Washington Metabolism and Transport drug interaction database (http://www.druginteractioninfo.org/). Thirty drugs involving 50 clinical DDI studies were chosen for this study, based on available data from clinical studies with midazolam. In vitro data reflecting competitive inhibition, time-dependent inhibition, and induction of CYP3A4 were collected from the scientific literature (Table 2). In vitro competitive inhibition data as well as time-dependent inhibition data used in this study were from enzyme kinetic data gathered using human liver microsomes. In vitro induction data used were from a human cryopreserved hepatocyte system. Of the 30 drugs used in this study, 13 drugs exhibited competitive inhibition with an IC₅₀ of less than 10 μM, 12 drugs exhibited time-dependent inactivation, and 11 compounds exhibited induction. Five drugs exhibited all three interaction mechanisms in vitro (troleandomycin, fluoxetine, mibefradil, saquinavir, and verapamil).

CYP3A4 Prediction Mathematical Equation. The equation used to predict the magnitude of DDIs, expressed as the ratio of area under the exposure-time curve in the presence (AUC′_p.o.) and absence (AUC_p.o.) of a pharmacokinetic drug-drug interaction, was reported previously (Fahmi et al., 2008b) and as the net effect equation below. This combined mathematical model is based on calculating the net effect of competitive inhibition, inactivation, and induction in both the intestine and liver:

Net effect equation: 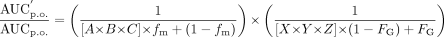where A is the term for time-dependent inhibition for the liver, B is the term for induction for the liver, 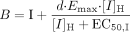C is the term for reversible inhibition in the liver, 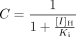X is the term for time-dependent inhibition for the intestine, 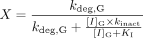Y is the term for induction for the intestine, 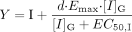and Z is the term for reversible inhibition for the intestine, [I]_G and [I]_H represent concentrations of inhibitor relevant for the intestine and liver, respectively. For the intestine, [I]_G was estimated using the equation described by Rostami-Hodjegan et al. (2004) for all calculations. For liver, free systemic C_max was used for the inactivation (term A) and induction (term B) portions of the expression, whereas free portal C_max was used for the reversible inhibition portion of the expression (term C). The true numerical value for CYP3A4 enzyme degradation rate, k_deg, can make a huge impact on the prediction, but it cannot be directly measured in humans in vivo. A wide variety of values of k_deg have been published (Thummel and Wilkinson, 1998; Venkatakrishnan et al., 2003; Galetin et al., 2006; McGinnity et al., 2006; Riley et al., 2007; Yang et al., 2008). In previous reports, the values used for k_deg were derived from modeling the time course of reversal of DDIs caused by induction or inactivation of P450 enzymes in human study subjects. Values used most currently for the degradation rates for CYP3A4 (k_deg) are 0.00032 min^–1 based on t_1/2 = 36 h and 0.00048 min^–1 based on t_1/2 = 24 h for the liver and intestine, respectively (Obach et al., 2005, 2007; Fahmi et al., 2008b). E_max, EC₅₀, and d represent the maximum -fold induction observed in cultured human hepatocytes, the concentration of inducer associated with half-maximum induction, and a calibration factor d (0.3), as described previously (Fahmi et al., 2008b).

The fraction of midazolam evading first-pass intestinal metabolism (F_G) has been estimated by several approaches and was well described by Galetin et al. (2008), where the reported value of F_G for midazolam ranged between 0.4 and 0.79 (Ito et al., 2004; Brown et al., 2006; Chien et al., 2006; Galetin et al., 2008). In this study, the value used for F_G was 0.57 (Obach et al., 2007), which is closer to the default midazolam value embedded in Simcyp (0.5). In this study, the value used for the fractional contribution of CYP3A4 to the metabolism of midazolam in the liver (f_m) was 0.93 (Obach et al., 2007) and the value embedded in Simcyp is 0.99.

Simcyp. The Simcyp Population-Based ADME Simulator (version 7.1; Simcyp Ltd., Sheffield, UK) was used to perform time-based and steady-state simulations of clinical drug-drug interaction studies according to the referenced publications or from Pfizer internal clinical study reports. A northern European white population was used for the demographics data as provided in the software, and specific study designs were replicated with respect to age range, gender ratio, and number of subjects. Model input parameters for midazolam were used as supplied in the software. Model input parameters for the following precipitant drugs were used as defined in the software: fluconazole, ketoconazole, terbinafine, fluvoxamine, diltiazem, erythromycin, fluoxetine, saquinavir, verapamil, and itraconazole. For the other precipitant drugs (roxithromycin, gatifloxacin, simvastatin, azithromycin, clarithromycin, cimetidine, atomoxetine, chlorzoxazone, ranitidine, mibefradil, troleandomycin, nefazodone, parecoxib, valdecoxib, atorvastatin, carbamazepine, rifampin, and conivaptan), input parameters were obtained from various literature sources or estimated (Table 1). The predicted effects of coadministration of the various CYP3A4 precipitants on midazolam exposure were determined using Simcyp, with which simulations were carried out using two different approaches, time-based and steady-state. Each drug was simulated with 10 trials and 10 subjects, which led to a total of 100 simulations for each combination.

Comparisons of Model Predictability. The bias of the prediction models was assessed from the geometric mean-fold error (GMFE), which equally weighs over- and underpredictions, and the root mean square error (RMSE) was calculated to provide a measure of the precision for the predictions: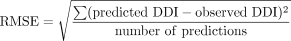

Results

The in vivo drug-drug interaction data gathered from the University of Washington database and used in this study are summarized in Table 1. Thirty drugs involving 50 midazolam clinical DDI studies were included in this study. In eight of the clinical studies, midazolam was administered intravenously (flumazenil, parecoxib, atorvastatin, fluconazole, gatifloxacin, ketoconazole, nitrendipine, and saquinavir). Two precipitant drugs, flumazenil and parecoxib, were administered intravenously. Based on clinical outcome, inhibitors were classified on the basis of the magnitude of the interaction according to the Food and Drug Administration Draft Guidance published in September 2006 (Guidance for Industry: Drug Interaction Studies: Study Design, Data Analysis and Implications for Dosing and Labeling, http://www.fda.gov/cder/guidance/6695dft.pdf). Two precipitant drugs, namely, carbamazepine and rifampin, were classified as strong inducers, which precipitated a significant AUC decrease in midazolam exposure. Eight precipitant drugs, namely, clarithromycin, conivaptan, itraconazole, ketoconazole, mibefradil, nefazodone, saquinavir, and troleandomycin, were classified as strong inhibitors, which precipitated an AUC increase in midazolam exposure of more than 5-fold. Seven precipitant drugs, namely, clarithromycin, conivaptan, diltiazem, erythromycin, fluconazole, saquinavir, and troleandomycin were classified as moderate CYP3A4 inhibitors, which precipitated an increase in the midazolam AUC of ≥2- but <5-fold. Twenty-two clinical studies, in which AUC ratios were 0.8 to 2 in the presence of precipitant drug, showed weak to no drug-drug interactions. Dependent on precipitant dose, as in the cases of clarithromycin and conivaptan, increased dose led to an increase in the magnitude of clinical DDIs, as expected. In addition, fluconazole, ketoconazole, and saquinavir yielded a reduced increase in midazolam exposure when midazolam was dosed intravenously compared with orally because of the elimination of first-pass intestinal metabolism.

In vitro data reflecting competitive inhibition, time-dependent inactivation, and induction of CYP3A4 were collected from the scientific literature (Table 2). Of the 30 drugs used in this study, 13 drugs exhibited competitive inhibition with an IC₅₀ of less than 10 μM, 12 drugs exhibited time-dependent inactivation, and 11 compounds exhibited induction. Five drugs exhibited all three interaction mechanisms in vitro (troleandomycin, fluoxetine, mibefradil, saquinavir, and verapamil).

To account for all known mechanisms affecting CYP3A4 activity, data from the three possible mechanisms (induction, inactivation, and competitive inhibition) were used simultaneously to make a prediction on the AUC ratio change. Table 3 shows the AUC ratio predictions by application of the combined model (Fahmi et al., 2008b) and the two models of Simcyp.

Although DDIs were predicted in all cases with a varying degree of accuracy (Fig. 1; Tables 3 and 4), no false-positive cases were observed. However, a few examples of significant overprediction of the magnitude of DDIs were observed with fluoxetine and ketoconazole based on all models, roxithromycin and mibefradil based on Simcyp models, and fluconazole based on the mathematical model. Also a few examples of significant underprediction of DDIs were observed with conivaptan (Simcyp) and troleandomycin (mathematical model). The most significant overprediction (138 versus 9) was noted with mibefradil when Simcyp was used under steady-state conditions. The clinical pharmacokinetics for midazolam in the clinical midazolam-mibefradil DDI (Veronese et al., 2003) show a pattern different from that predicted by Simcyp in that the midazolam concentrations 24 h postdose are significantly higher using the Simcyp prediction than were observed clinically. In contrast, the midazolam levels were still high at 24 h in the Simcyp time-based simulation. Thus, although the time-based DDI simulation looks superior to that of the steady-state simulation, the Simcyp midazolam profile in the presence of mibefradil does not match the clinical profiles. In summary, there are a number of factors that could be contributing to overprediction of the DDI by Simcyp.

The combined mathematical model and steady-state and time-bound Simcyp approaches predicted a “correct” DDI result (interaction or no interaction, defined as a 2-fold change in exposure) in 44, 44, and 45 of the 50 trials, respectively. The corresponding GMFE values were calculated as 1.74, 1.59, and 1.47, for the combined mathematical model, steady-state, and time-bound approaches, respectively, as shown in Table 4. Of the trials that had a clinical DDI effect ≥2-fold (n = 27), the increase in AUC was predicted within 50% of the actual value in 21, 21, and 24 of the trials for the combined mathematical model, steady-state, and time-based approaches, respectively. The corresponding GMFE values were calculated as 1.88, 1.64, and 1.51 for the combined model, steady-state, and time-based approaches, respectively. Overall, the combined mathematical model and Simcyp yielded comparable performance in predicting in vivo DDIs from in vitro data.

• Download figure
• Open in new tab
• Download powerpoint

Fig. 1.

Predicted versus observed AUC ratios, assuming interaction in the liver and the intestine where prediction is based on the combined mathematical model (A), along with prediction using the Simcyp (version 7.1) steady-state approach (B) and time-based approach (C). •, compounds showing reversible inhibition in vitro; ○, compounds showing reversible inhibition and inactivation in vitro, ▾, compounds showing inhibition and induction; ▵, compounds showing all three mechanisms in vitro; ▪, compounds showing induction only in vitro.

Discussion

Drug-drug interactions caused by the effect of one drug on the clearance of a second drug are an important consideration in clinical practice. The use of concomitant medications for multiple indications in individual patients is commonplace, especially in elderly patients who have multiple medical problems. In some cases, more than one drug may be needed to treat multiple inter-related symptoms of a single disease (e.g., psychiatric disorders, cardiovascular disease, and cancer) or multiple drugs may be needed to treat challenging infections (e.g., human immunodeficiency virus and bacterial infections). CYP3A4 is the single most important drug-metabolizing enzyme and is involved in the clearance of more than half of drugs used clinically. Effects on CYP3A4 activity are the most frequent mechanisms of DDIs, and the pharmacopeia is rife with examples of drugs that inhibit, inactivate, and induce this enzyme. Thus, in the research and development of new pharmacotherapies, the prediction of pharmacokinetic DDIs is important, and in vitro approaches for prediction are valuable because they can be used in drug design and in selection of candidate compounds for further development with a reduced propensity for causing DDIs.

Over the past few years, considerable progress has been made in the development of approaches to predict DDIs from in vitro data. For the phenomena of reversible inhibition, irreversible inactivation, and induction, approaches to predict DDIs from in vitro data have been developed, but these different mechanisms have been approached separately. For irreversible inactivation, the pioneering work of Mayhew et al. (2000) defined relationships between inactivation parameters measured in vitro (k_inact and K_I) and in vivo parameters (plasma concentrations, k_deg) to predict the magnitude of CYP3A4 DDIs, including effects on activities in both liver and intestine (Mayhew et al., 2000; Wang et al., 2004). These concepts were extended to include other P450 enzyme targets (Obach et al., 2007). For reversible inhibition, correlation between in vivo DDIs and in vitro inhibition potency (K_i) was also demonstrated across a broad panel of P450 inhibitors, an important finding indicating that estimated portal vein C_max was a more accurate parameter to use for [I]_{in vivo} than systemic concentrations (Kanamitsu et al., 2000b; Obach et al., 2006). Prediction of the magnitude of DDI caused by enzyme inducers is even more challenging because the molecular mechanism is indirect (i.e., the inducer is not binding with the enzyme itself but acting on proteins involved in regulation of enzyme transcription). For CYP3A4 inducers, prediction of the magnitude of DDIs has been accomplished using a correlative approach using in vitro parameters E_max and EC₅₀, (Sinz et al., 2006; Fahmi et al., 2008a). However, in some instances, a compound can affect the activity of a given P450 enzyme by two or three of these mechanisms simultaneously. For example, ritonavir has been demonstrated to be a potent inhibitor and mechanism-based inactivator of CYP3A4 as well as a pregnane X receptor activator (Zhou, 2008). Prediction of DDIs for such an agent is challenging because it is difficult to ascertain which of the phenomena will dominate in the in vivo response and would require a clinical DDI study to determine what the effect will be. To that end, a “combined model” was proposed for CYP3A4-based DDIs for those compounds that exhibit reversible inhibition, inactivation, and induction (Fahmi et al., 2008b), and it was demonstrated to perform well in the prediction of DDIs.

However, most mathematical models provide point estimates of the average DDI, with the assumption of one precipitant concentration and the same in vitro inhibition kinetic parameters, effectively applying the same CYP3A4 enzyme level across the population. It is clear that there is a degree of uncertainty associated with using such data in that the risk to individuals is not evaluated. Although CYP3A4 is the most abundant P450 subfamily in human liver, its level of expression can vary enormously (>10-fold) among individuals. Therefore, using interindividual variability and having the ability to input details of study design in relation to exposure time during interaction studies are important factors in simulating a clinical study. In this situation, a computer-simulated program can have an advantage because the concentration used in the model is dynamic and changes with time along with the ability to choose a specific population (e.g., poor metabolizer, impaired renal function, or other) as well as using multiple subjects in the simulation representing the variable content of their drug-metabolizing enzymes. The approach involves the combination of the concepts used in these aforementioned prediction methods with population pharmacokinetic modeling to provide not only point estimates of DDI magnitudes but also simulation of DDI across different individuals and groups (Einolf, 2007; Rostami-Hodjegan and Tucker, 2007).

The Simcyp steady-state approach can potentially show the effect of population variability in DDIs and allow direct comparison with the combined mathematical model without accounting for trial design. The Simcyp time-based approach simulations permit concentration changes over time, mimicking actual trial design. Although there is no marked improvement using the time-based Simcyp approach, there is a trend toward better predictions in the parameters shown in Table 4 (versus both the combined model and the steady-state Simcyp model). Indeed, in some instances this is because of differences in the [I] concentrations used and also in the nature of the input values to the Simcyp models. However, there are differences in the way that the two models handle both reversible and time-dependent inhibitors. Einolf (2007) used the steady-state Simcyp model (referred to as “mechanistic static models,” which consider important mechanistic factors such as fractional metabolism (f_m) and the nature of interaction. However, because these models fix the concentrations of substrate at a lower level than K_m and fix the level of interacting drug (precipitant) for a given dose, they cannot account for any trial elements apart from the dose of inhibitor. Thus, dose staggering, a variable absorption rate for precipitant drugs, and the effect of volume of distribution on elimination rate and interaction cannot be investigated. The time-based approach referred to as the “mechanistic dynamic model” by Einolf (2007) assesses the concentration changes over time, which facilitates mimicking of actual trial design. Although the second model assesses time- and concentration-dependent enzyme inhibition using unbound systemic plasma concentrations that the liver encounters (i.e., portal vein concentration), the steady-state model uses two different “fixed” values of inhibitor concentrations for inhibiting the metabolism during first-pass and subsequent passes, namely, the highest portal vein concentration after the oral dose of the inhibitor and average steady-state concentrations in plasma after multiple oral doses at set intervals. The multiple differences between the model assumptions and their sensitivity (or lack of it) to certain parameters (volume of distribution, accumulation, dosing interval, and absorption rate) make it difficult to expect a uniform pattern regarding the predicted level of DDI when the results from the steady-state and time-based approaches are compared. However, a higher degree of confidence in the model can be obtained by visualization of the pharmacokinetic profile afforded by the time-based output and comparison with clinical data.

The objective of the present study was to determine the performance of the combined model and the population/simulation model (Simcyp) in the prediction of DDIs using midazolam DDI studies reported in the scientific literature as a test set. The population model can be useful in the identification of subgroups at greater risk for clinically relevant interactions. For instance, there is considerable variability in the expression of CYP3A4 and CYP3A5. Those individuals with a high expression of CYP3A4 will probably have a greater fraction of clearance of the victim drug via that pathway, and thus inhibition may have greater magnitude in these individuals. A total of 50 clinical DDI studies in which midazolam was the affected drug were gathered from the literature with 30 drugs tested as precipitants of these interactions. The interactions ranged from a 16-fold increase caused by ketoconazole to a 96% decrease caused by carbamazepine, with several drugs causing no interaction. The combined model yielded a good success rate for predicting these DDIs, with a mean -fold error of 1.74 and a rate of success (i.e., correctly categorizing a DDI based on a boundary of 2-fold) of 88% (44 of 50 correct) (Table 4). Simcyp version 7.1 offers two simulation approaches referred to as “steady-state” and “time-based.” From this dataset, it appeared that the time-based approach performed somewhat better, with a mean -fold error of 1.47 versus 1.59. However, the steady-state approach results were skewed by a single outlier prediction (Table 4). Success rates for categorizing DDIs as less than or greater than 2-fold was more than 88% for both models. The performance of Simcyp in this study was similar to that described by Einolf (2007) for a different set of DDI studies. Overall, both the combined mathematical model and the Simcyp models performed well in the estimation of CYP3A4-based midazolam DDIs from in vitro data, and these would be useful in prospective prediction of CYP3A4 DDIs for new compounds.

In the combined model, it was found that the reversible inhibition portion performed the best when the unbound portal vein concentration was used for [I]_{in vivo}, whereas for irreversible inactivation and induction, the unbound systemic concentration was best (O. A. Fahmi and R. S. Obach, unpublished results). Although on the surface this finding may seem inconsistent, from a physiological perspective it can be rationalized. For reversible inhibition, it is more common for the interaction to be exhibited by an increase in C_max (and hence AUC) but not an effect on t_1/2, particularly with higher clearance drugs. This result indicates that much of the interaction occurs during absorption and the hepatic first pass. After the first pass is complete, the concentrations of inhibitor are diluted to values below these needed to exhibit reversible interaction. Estimated unbound portal vein concentrations were also demonstrated to be the most appropriate concentrations in previous work (Obach et al., 2006). For inactivation and induction, systemic concentrations were most appropriate. This use also makes sense in that the DDIs caused by inactivators and inducers occur on C_max, AUC, and t_1/2 of the affected drug, indicating that the biochemical effect continues to occur after first-pass exposure of the intestine and liver is over. In previous methods in which different values for [I]_{in vivo} were considered for inactivation, the free systemic concentration provided the most accurate predictions (Obach et al., 2007) and for induction this was also the case in some investigations (Fahmi et al., 2008a; Shou et al., 2008) but not others (Sinz et al., 2006). In the Simcyp models, the precise values used for [I]_{in vivo} are embedded within the software, and the sophistication of the software permits the value for [I]_{in vivo} to be dynamic, which is physiologically more realistic.

It should be noted that some of the parameters used by Simcyp and the combined model differ, such as the values for f_m (CYP3A) in the liver. Therefore, some of the performance difference, albeit small, could be due to these different parameters. For example, the combined mathematical model uses a hepatic f_m value of 0.93 for midazolam metabolism, whereas Simcyp has an embedded value of 0.99. The sensitivity of prediction of DDIs to the f_m parameter, particularly when that value exceeds 0.9, is well established. In the comparison we have made between Simcyp and the combined mathematical model, our intent was to compare Simcyp as an out-of-the-box application using the parameters embedded in the program. We do not have an explanation for the observation that f_m 0.93 worked with the combined model and 0.99 worked in Simcyp.

Overall, our conclusions are that both the combined mathematical model and computer simulation approaches successfully predict the magnitude of CYP3A4-based DDIs, even when the precipitant drug has multiple simultaneous actions (inhibition, inactivation, and/or induction). When the precipitant drug has just one mechanism of action, other, more simple, approaches can be used, and in these cases the combined model simplifies to algorithms possessing just one of the interaction terms. Ongoing efforts include the application of this model to DDIs for other CYP3A4-cleared drugs besides midazolam as well as application to other P450 enzymes (although in the latter case the number of examples of in vivo DDIs caused by multiple mechanisms are far fewer). Results of these investigations will be reported in due course.