Advertisement
Research ArticleArticle

Physiologically Based Pharmacokinetic Modeling of Intestinal First-Pass Metabolism of CYP3A Substrates with High Intestinal Extraction

Michael Gertz, J. Brian Houston and Aleksandra Galetin
Drug Metabolism and Disposition September 2011, 39 (9) 1633-1642; DOI: https://doi.org/10.1124/dmd.111.039248

Abstract

Prediction of intestinal availability (FG), in conjunction with hepatic metabolism, is of considerable importance in drug disposition to assess oral clearance and liability to drug-drug interactions. In the current study, FG predictions were performed within a physiologically based pharmacokinetic (PBPK) model using in vitro permeability and clearance data. The prediction success was assessed in comparison with the QGut model. In addition, apparent oral clearance values, predicted using the PBPK model, were compared with in vivo observations from meta-analyses. Finally, unbound intrinsic clearance values (CLuint) were determined for 12 CYP3A substrates in eight individual human jejunal microsome (HJM) samples to assess interindividual variability in intestinal intrinsic clearance and subsequent FG predictions. Overall, the PBPK model improved FG predictions in comparison with the QGut model; this was apparent by a reduced bias and increased precision. In particular, FG predictions of indinavir, saquinavir, and terfenadine were model-dependent. The predicted oral clearance values of the drugs investigated ranged from 8.79 to 6320 l/h for tacrolimus and simvastatin, respectively, and were overall within 3-fold of the observed data with the exception of indinavir, atorvastatin, and buspirone. The individual HJM CLuint values ranged from 17 to 14,000 μl · min−1 · mg−1 for atorvastatin and saquinavir, respectively, and corresponding interindividual variability in CLuint estimates ranged from 41 to 67%. These in vitro data resulted in predicted FG values ranging from 0.03 to 0.94 for simvastatin and indinavir, respectively. The largest interindividual variability of FG was predicted for terfenadine (65%) in contrast with the low variability in the case of indinavir (3%).

Introduction

CYP3A enzymes represent the principle drug-metabolizing enzymes in the small intestine (Paine et al., 1997, 2006). The expression levels of CYP3A along the small intestine decline from the proximal to the distal regions (Paine et al., 1997; Zhang et al., 1999). A high drug concentration in the enterocytes during the absorption phase may lead to substantial metabolism despite the relatively low enzyme content (∼1% in comparison to the liver) (Paine et al., 1997). On the other hand, it may lead to saturation or in some instances to inhibition of metabolism, resulting in nonlinear pharmacokinetics after oral drug administration. In addition, small intestinal metabolism is associated with substantial interindividual variability. For example, an up to 10-fold range in individual activity was demonstrated using metabolite formation data in the case of cyclosporine and tacrolimus (Lampen et al., 1995, 1996), which may partially reflect the high interindividual variability of CYP3A abundance (von Richter et al., 2004; Paine et al., 2006).

The importance of intestinal metabolism may be delineated from clinical studies after intravenous and oral drug administration or, alternatively, from grapefruit juice interaction studies under appropriate conditions. However, both in vivo methods are flawed by a number of inherent limitations discussed elsewhere (Galetin et al., 2008; Gertz et al., 2008a). The intestinal availability (FG) for drugs such as cyclosporine, midazolam, felodipine, and tacrolimus is based on a considerable number of studies, in contrast to very limited and variable data for buspirone, statins, saquinavir, and terfenadine; hence, the in vivo FG estimates for the latter drugs have to be regarded with caution. In addition, in vitro data may be used to make predictions of intestinal metabolism based on either in vitro clearance alone (Shen et al., 1997) or in combination with permeability data (Yang et al., 2007; Gertz et al., 2010). For the prediction of intestinal metabolism, the enterocytic, rather than the total intestinal blood flow, needs to be incorporated (Tam et al., 2003). The rationale for using enterocytic blood flow in the FG predictions is that drugs pass through the enterocytes which contain the majority of metabolically active enzymes in the small intestine (Kolars et al., 1994). In general, no binding to enterocytic proteins is assumed, although this has not been satisfactorily investigated and is in contrast to the assumptions of the well stirred model for the liver. Advancement in computational power has allowed incorporation of intestinal transit times and heterogeneous expression levels of CYP3A into mechanistic predictions of intestinal absorption and metabolism. Complex models to predict intestinal absorption generally represent adaptations of the compartmental absorption and transit model (Yu and Amidon, 1999) and may account for drug dissolution, solubility, permeability, transport, and metabolism (Agoram et al., 2001; Tam et al., 2003; Jamei et al., 2009). Limiting the current trend toward holistic and mechanistic data interpretation is the need for extensive in vitro studies (e.g., full kinetic characterization of drug affinity for metabolizing enzymes and transporters) and formulation-specific data (e.g., dissolution and solubility) in conjunction with the quality of physiological information (e.g., abundance data of relevant enzymes and transporters) to support these models.

To reduce the necessary in vitro input data, previous work investigated FG prediction success using the QGut model, which simplifies prediction of intestinal metabolism to the input of in vitro clearance and permeability data (Yang et al., 2007; Gertz et al., 2010). The QGut model has the basic structure of the well stirred model; however, the blood flow term is modified to represent a hybrid parameter, QGut, consisting of physiological flow (i.e., enterocytic blood flow) and drug permeability (Chalasani et al., 2002; Rostami-Hodjegan and Tucker, 2002). However, our analysis highlighted considerable bias and imprecision in the prediction of FG for drugs with in vivo FG values less than 0.5 (Gertz et al., 2010). In particular, the QGut model predictions of FG for indinavir, saquinavir, and terfenadine were underpredicted by up to 96%. Thus, a physiologically based pharmacokinetic (PBPK) model was developed, which retains the use of in vitro clearance and permeability data but overcomes some of the limitations of the QGut model. The PBPK model takes into account heterogeneity of metabolizing enzymes, drug concentration in the enterocytes, and any potential saturation of intestinal metabolism. The latter in particular was assumed to be responsible for some of the FG underprediction trends observed previously. Prediction success of the PBPK model is assessed in comparison with the QGut model using 12 CYP3A drugs with low intestinal availability in vivo. In addition, apparent oral clearance is predicted for the selected drugs using the PBPK modeling approach and compared with in vivo observations from meta-analyses. Finally, eight individual human jejunal microsome (HJM) samples are used to determine in vitro intrinsic clearance data of 12 selected drugs to assess interindividual variability in FG predictions.

Materials and Methods

Determination of Intestinal Clearance In Vitro.

In vitro clearance data were determined by substrate depletion in eight individual human jejunal microsomal samples prepared by an elution method from white donors. The microsomes from individual jejunal donors were purchased from BD Gentest (Woburn, MA) (Table 1). Substrate depletion experiments were performed in 0.1 M phosphate buffer (pH 7.4) containing 10 mM MgCl2, 7.5 mM isocitric acid, 1.2 units/ml isocitric acid dehydrogenase, and 1 mM NADP. The microsomal protein concentrations ranged from 0.025 to 1.5 mg/ml for lovastatin/simvastatin and cyclosporine, respectively. The substrate concentrations were 10-fold below the reported Km values in the literature for the drugs investigated. The drugs were added from methanol stock solutions, resulting in a final concentration of organic solvent in the incubation of 0.1% v/v. Clearance incubations were prepared as replicates of two in Eppendorf tubes at 37°C and 900 rpm in an Eppendorf Thermomixer. The metabolic reaction was initialized by the addition of NADP solution to the incubation mixture, and samples were taken at six designated time points within 60 min. Noncytochrome P450-dependent loss of drug over the incubation time was monitored by preparing additional samples in the absence of NADP. Metabolic reactions were terminated by removal of aliquots into an equal volume of ice-cold acetonitrile containing internal standard. Samples were centrifuged at 1000g for 20 min at 4°C in a Mistral 3001 centrifuge [MSE (UK) Ltd., London, UK], and 150 μl of supernatant was removed from each Eppendorf vial and transferred to glass vials before analysis on the LC-MS/MS system. Detailed information on LC-MS/MS analysis and the list of chemical suppliers have been reported in our previous publication (Gertz et al., 2010). Clearance values were corrected for experimentally determined nonspecific binding values to microsomal protein (fuinc) (Gertz et al., 2008b, 2010). For cyclosporine, binding was predicted using drug lipophilicity data. The unbound intrinsic clearance values, CLuint, were calculated using eq. 1. Clearance values were corrected for the mean population CYP3A abundance in the intestine of 50 pmol of CYP3A/mg protein (Paine et al., 2006) prior to FG predictions. Embedded Image where k represents the depletion rate constant, V represents initial incubation volume, and proteinmicrosomal represents the initial amount of protein.

View this table:
TABLE 1

Summary of individual human jejunal microsome preparations

Testosterone 6β-Hydroxylation Activity.

CYP3A enzyme activities of the HJM were determined at 250 μM testosterone concentration (substrate concentration sufficient to achieve Vmax conditions) monitoring 6β-hydroxytestosterone formation over 10 min at a microsomal protein concentration of 0.5 mg/ml. Aliquots of 100 μl were removed into 100 μl of ice-cold acetonitrile containing progesterone (1 μM) as an internal standard. The appearance of 6β-hydroxytestosterone (m/z, 305.15 > 269.3, cone voltage 80 V, and collision energy 15 eV at maximum cone gas flow) was monitored. The LC-MS/MS system used consisted of a Waters 2795 with a Micromass Quattro Ultima triple quadruple mass spectrometer (Waters, Milford, MA). A Luna C18 column (3 μm, 50 × 4.6 mm) was used for chromatographic separation of the analytes using a gradient of acetonitrile and water containing 0.05% v/v formic acid. Composition of cofactors was the same as that in the substrate depletion assay; organic solvent content was 0.3% v/v methanol. Activity determination was performed on three separate occasions to assess interday variability.

Determination of Km Values.

Michaelis-Menten constants were determined for four drugs for which the literature indicated low and variable Km values. Substrate depletion clearance was determined at the following substrate concentration ranges: felodipine, 0.5 to 10 μM (6 concentrations); indinavir, 0.025 to 5.5 μM (10 concentrations); nisoldipine, 0.25 to 5.0 μM (6 concentrations), and saquinavir, 0.05 to 5.0 μM (6 concentrations). The depletion profiles at the different substrate concentrations were performed in one representative microsomal preparation, HJM 6 (chosen for its high testosterone 6β-hydroxylation activity and low between-day variability). The CLuint and Km values together with associated S.E.s were determined using eq. 2 (Obach and Reed-Hagen, 2002). The equation reported by the original investigators was modified by multiplying both sides of the equation with the volume of incubation to transform depletion rate constants to intrinsic (at [S] approaching 0) and apparent intrinsic clearance (at any [S]). The fitting was performed in Grafit 5.0.10 (Erithacus Software Limited, Horley, Surrey, UK). Embedded Image where CLuint represents the unbound intrinsic clearance, CLuint, app is apparent intrinsic clearance, [S] is substrate concentration, and Km is the Michaelis-Menten constant.

Preliminary Assessment of Enterocytic Drug Concentration and Possible Saturation of First-Pass Metabolism.

Indinavir, saquinavir, and terfenadine FG values were previously considerably underpredicted by 75 to 96% using the QGut model (Gertz et al., 2010). Unlike the PBPK model, the QGut model predictions did not take enterocytic concentrations (Cent) into account. An initial assessment of enterocytic drug concentration was performed on the basis of eq. 3. Embedded Image

The doses (D), absorption rate constants (ka), and fractions absorbed (Fa) considered for the preliminary analyses are summarized in Table 2; an enterocytic blood flow (Qent) of 18 l/h was assumed. The selection of doses and formulations was based on the studies from which in vivo FG estimates were obtained. The drugs investigated were ranked for their likelihood that saturation may have biased previous FG estimates by assuming linearity in the QGut model. From this analysis, a minor bias of intestinal metabolism can be anticipated by neglecting saturation of intestinal metabolism (Cent/Km < 1) for atorvastatin, felodipine, midazolam, and tacrolimus. In contrast, saturation was anticipated to affect the assessment of intestinal metabolism for cyclosporine, indinavir, saquinavir, and terfenadine to a greater extent (Cent/Km > 10). In addition, for indinavir, saturation of hepatic first-pass metabolism was anticipated. In fact, saturation of systemic clearance of indinavir (radiolabeled intravenous dose) was shown with concomitant administration of 400 to 800 mg of indinavir orally (Yeh et al., 1999). Equation 3 does not allow assessment of regional differences in Cent and subsequent effects on FG.

View this table:
TABLE 2

Summary of drug-related parameters used in the current PBPK model for 12 drugs investigated

References for logPo:w, pKa, fup, ka, and Km are found in Supplemental Table 1 and at http://www.pharmacy.manchester.ac.uk/capkr/.

Reassessment of Atorvastatin FG after Intravenous/Oral Administration.

The in vivo estimate of atorvastatin FG was reassessed on the basis of the available blood/plasma concentration ratio data (Rb = 0.61; Table 2). The initial assessment of atorvastatin FG was based on the assumption of Rb being equivalent to 1 (Lennernäs, 2003), which resulted in a lower hepatic extraction ratio in comparison with the current analysis (0.42 versus 0.63) and subsequently a lower estimate of FG (0.24 versus 0.38). The current FG estimate of 0.38 assumes complete absorption of atorvastatin (Lennernäs, 2003). The reevaluation of atorvastatin FG from intravenous/oral data compared favorably to data from grapefruit juice interaction studies (Gertz et al., 2008a).

Reassessment of Intrinsic Clearance of Cyclosporine and Tacrolimus.

In comparison with Gertz et al. (2010), the unbound fractions in plasma of cyclosporine and tacrolimus were reevaluated from the available literature. Different methods have been used to determine both cyclosporine and tacrolimus fraction unbound in plasma. The current study favored fup measurements determined in stainless steel equilibrium dialysis chambers for cyclosporine (1.9%) and tacrolimus (1.3%), given their high reproducibility. The use of these fup values resulted in changed estimates of in vivo CLint, h in comparison to our previous publication (Table 2).

PBPK Model to Estimate FG and CLoral from In Vitro Data.

A PBPK model was constructed in which tissues were connected by an arterial blood supply and a collective venous return to the lungs (Nestorov, 2003). All tissues were considered to be well stirred compartments, i.e., that the unbound tissue concentration is at equilibrium with the unbound concentration in the emergent blood (eq. 4). 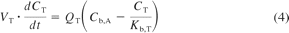Embedded Image where VT, CT, QT, and Kb, T represent the volume, concentration, blood flow, and tissue/blood concentration ratio of the different tissues and Cb, A represents the arterial blood concentration.

The physiological values for blood flows and tissue volumes were taken from the literature (Brown et al., 1997; International Commission on Radiological Protection, 2002). The selected tissues accounted for >95% of total body weight; an additional compartment representing the rest of the body was included. Tissue/blood concentration ratios were either collated from the literature or predicted with mechanistic equations (Rodgers et al., 2005; Rodgers and Rowland, 2006) using human tissue composition data (Poulin and Theil, 2002). For tissues where no human data were available, rat tissue composition data were used. Concentration-time profiles, as well as FG and CL parameters, were taken into consideration in the model development using midazolam and alfentanil as test compounds because of availability of Kb data in rat (data not shown). However, subsequent analysis focused on the prediction of FG, CLi.v., and CLoral.

The intestinal and liver compartments of this model are outlined in detail below, as they allowed the assessment of intestinal and hepatic availability and apparent intravenous and oral clearance. Systemic clearance was considered to occur exclusively in the liver (unless renal excretion was significant, e.g., for indinavir) and presystemic metabolism was considered to occur in both the small intestine and the liver. The liver was separated into liver tissue and the blood residing in the liver. The rate equations (eqs. 5 and 6) describe the change in concentrations in liver blood and liver tissue, respectively. 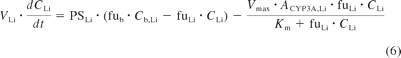Embedded Image Embedded Image where Cb, A, Cb, PV, CLi, and Cb, Li represent the concentrations in the arterial blood, portal vein, liver, and hepatic outlet (or liver blood), respectively; Qb, HA (6.5% of cardiac output), Qb, PV (18.5% of cardiac output), and Qb, HV (Qb, HA + Qb, PV) represent the blood flows of the hepatic artery, portal vein, and hepatic vein, respectively; fub and fuLi represent the fractions unbound in blood and liver (fuLi = fub/Kb, Li for drugs with no active uptake or efflux); Vb, Li and VLi represent the volumes of the blood residing in the liver and the liver tissue, respectively; PSLi, Vmax, and Km represent the permeability-surface area product (10,000 times greater than hepatic blood flow to satisfy perfusion limited assumptions), the maximum metabolic velocity, and the Michaelis-Menten constant for metabolism, respectively; and ACYP3A, Li represents the total hepatic amount of CYP3A.

In the current analysis, no active uptake or efflux was considered to occur in the liver for the drugs under investigation. However, eqs. 5 and 6 can be modified to accommodate these processes by inclusion of the appropriate Michaelis-Menten or intrinsic clearance terms and accounting for the extracellular water fraction. The portal vein concentration represents the differential of emergent blood concentrations from the intestine (including the enterocytes), stomach, spleen, and pancreas.

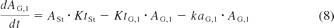
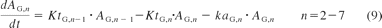
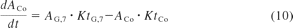
The small intestine was divided into seven compartments (Fig. 1): 1, 2 to 3, and 4 to 7 represent the intestinal segments of duodenum, jejunum, and ileum, respectively (Yu and Amidon, 1999). The rate equations below describe the change of drug amount in the stomach and intestinal lumen (eqs. 7–10) and drug concentration in the enterocytes (eq. 11) with respect to time. 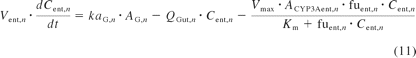Embedded Image Embedded Image Embedded Image Embedded Image Embedded Image where A denotes the amounts of drug in either the stomach (ASt), the intestinal segments (AG, n), or the colon (ACo); KtSt, KtG, n and KtCo refer to the transit rate constants of stomach, intestinal lumen, and colon, respectively; ka represents the absorption rate constant determined using eq. 15; fuent, Cent, n, Vent, n, ACYP3A,ent,n, and QGut, n refer to the unbound fraction, concentration, volume, amount of CYP3A, and the hybrid parameter of blood flow and permeability in the enterocytes of the nth intestinal compartment.

Fig. 1.
Fig. 1.

Illustration of the absorption model applied for the current analyses. First (gray) and second levels represent undissolved and dissolved drug (after immediate release) in the different segments of the intestinal lumen, respectively; third level: enterocytes. St, stomach; D, duodenum; J1–2, jejunal segments; I1–4, ileal segments; Kt, transit rate constants; ka, absorption rate constants; CL, apparent intrinsic clearance in the different intestinal segments, QGut, hybrid function of regional enterocytic blood flows and drug permeability; Qent, total enterocytic blood flow.

Drug permeability was incorporated as a hybrid parameter of enterocytic blood flow and permeability, as in the QGut model (Chalasani et al., 2002; Rostami-Hodjegan and Tucker, 2002). Absorption was considered to occur from the small intestinal compartments with the exception of saquinavir, for which colonic absorption was also incorporated, as investigated previously (Agoram et al., 2001). The blood flow to the small intestine represents approximately 10% of the cardiac output (39 l/h) (International Commission on Radiological Protection, 2002), and the enterocytic blood flow represents approximately 50% (i.e., 18 l/h) of the small intestinal blood flow (Granger et al., 1980). The cardiac output in the current assessment was 6.5 l/h, based on male subjects aged 20 to 35 years (Brown et al., 1997; International Commission on Radiological Protection, 2002). Effect of age on cardiac output (Brown et al., 1997) was taken into account for tacrolimus FG predictions.

Intestinal availability, apparent intravenous, and oral clearance data were calculated from eqs. 12 and 13; where t-last represents a time appropriate to completely recover the administered dose as metabolites or drug excreted unchanged and AMent, n represents the accumulative amount metabolized in the nth enterocyte compartment. The rate equations was solved in Matlab (version 7.10, 2010) using the ODE15s or 23s solvers. A mass balance equation was included in the script to allow monitoring of dose recovery over time. 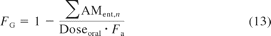Embedded Image Embedded Image where C(t) represents the drug concentration-time profile in blood or plasma, Fa represents fraction absorbed, and FG represents the fraction of drug amount available to the enterocytes that enters the portal vein unchanged.

The main assumptions made in the current analysis are as follows: 1) there is no contribution of the small intestine to the systemic elimination of drugs; 2) there is no binding of drugs in the enterocytes (i.e., fuent = 1); 3) drug distribution into tissues satisfies the well stirred assumptions (no active uptake or efflux); 4) CYP3A is exclusively responsible for the metabolism of selected drugs; 5) dissolution and solubility do not affect assessment of FG (special considerations for cyclosporine, indinavir, saquinavir, and terfenadine are outlined below); and 6) absorption occurs from the seven compartments of the small intestine only, with the exception of saquinavir for which colonic absorption was also incorporated.

Parameters for PBPK Modeling.

The metabolism in the liver was scaled using the standard human microsomal recovery of 40 mg/g, average liver weight of 21.4 g/kg, and CYP3A content of 155 pmol/mg microsomal protein. The total CYP3A contents in the duodenum, jejunum, and ileum were 9.7, 38.4, and 22.4 nmol, respectively (Paine et al., 1997). The regional weights of the enterocytes and the transit rate constants in the duodenum, jejunum, and ileum were 18.2 g and 4.3 h−1, 65.8 g and 1.7 h−1, and 38.3 g and 2.1 h−1, respectively (Yu et al., 1996; Paine et al., 1997). Differential blood supply to the duodenum, jejunum, and ileum was accounted for (Jamei et al., 2009; Darwich et al., 2011).

The oral absorption rate constants (ka) of the drugs investigated here were estimated from apparent permeability data determined in MDCK-MDR1 cells. These data were first converted to effective permeability, Peff, using the regression analysis previously performed on a set of 20 drugs (eq. 14) (Gertz et al., 2010). The Peff data were then used to estimate absorption rate constants by eq. 15 (Yu and Amidon, 1999). The radii of the different intestinal compartments (rSI) ranged from 0.85 and 1.58 cm for the ileum and duodenum, respectively (default values in GastroPlus version 7).

Embedded Image Embedded Image

For cyclosporine, indinavir, saquinavir, and terfenadine, saturation of intestinal metabolism was considered highly likely on the basis of preliminary analysis. Drug solubility data were therefore incorporated for these drugs, because luminal solubility may limit drug concentration in the enterocytes. In those cases, luminal rate equations (eqs. 7–10) were expanded to include the dissolved and undissolved drug amounts (Hintz and Johnson, 1989), as exemplified in eqs. 16 and 17. The current model assumed immediate drug release, dissolution from spherical particles, a constant particle radius over time, and equality of dissolution and precipitation rate constants. The occurrence of supersaturation was allowed. 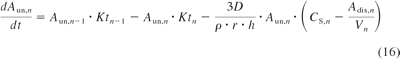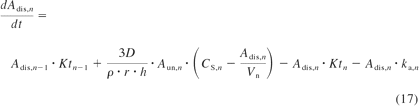Embedded Image Embedded Image where Aun and Adis represent, respectively, the undissolved and dissolved amount in the intestinal compartment n (including stomach and colon); Ktn and kan represent the transit rate and absorption rate constants of the nth compartment; D represents the diffusion coefficient; ρ is the density; r is the particle radius; h is the diffusion layer thickness; CS, n is drug solubility in the nth is luminal compartment; and Vn is luminal volume of the different intestinal segments (default values in GastroPlus version 7).

For these four drugs, measurements in fasted simulated small intestinal fluids were kindly provided by Pfizer (Pharmacokinetics, Dynamics and Metabolism group, Sandwich, UK); additional solubility profiles across different pH values, if available, were obtained from the literature (Supplemental Table 1). The diffusion coefficients were estimated from molecular weights, the diffusion layer thickness was considered to be equal to particle radius (Hintz and Johnson, 1989), and a density of 1.2 g/ml was used (default value in GastroPlus version 7 and SimCYP version 10). A summary of drug solubility and particle size used can be found in Table 3.

View this table:
TABLE 3

Drug solubility data obtained in fasted simulated small intestinal fluids and particle size for cyclosporine, indinavir, saquinavir, and terfenadine

Additional references are found in Supplemental Table 1.

Michaelis-Menten constants for CYP3A metabolism were collated from the literature except for felodipine, indinavir, nisoldipine, and saquinavir, for which Km data were determined in the current study. A summary of Km data, physicochemical properties, and drug permeability and clearance data used in the current analysis is provided in Table 2.

In vitro intrinsic clearance data used for predictions were determined in either pooled intestinal and liver microsomes (Gertz et al., 2010) or eight individual HJM reported in the current study. The clearance data obtained in the intestinal and liver pools were used for a comparison of model performance between the FG predictions by the QGut and the PBPK model and for the prediction of apparent intravenous and oral clearance using the PBPK model. On the other hand, the individual HJM data were used to assess interindividual variability in FG predictions using the PBPK model alone.

Measurement of Prediction Success and Comparison with In Vivo Data and QGut Predictions.

The predictions of FG and apparent intravenous and oral clearance data were compared with corresponding in vivo data summarized in Table 4. Bias and precision of FG and clearance predictions were assessed by geometric fold error and root mean squared error.

Results

Small intestinal metabolism was assessed for 12 drugs in eight individual human jejunal microsomal preparations (six male and two female white donors) (Table 1). The mean CYP3A activity was 4.12 nmol · min−1 · mg−1, ranging from 2.09 to 5.88 nmol · min−1 · mg−1 as measured by formation of 6β-hydroxytestosterone at 250 μM testosterone concentration. The mean CYP3A activity was associated with a coefficient of variation of 36%; a 2.8-fold difference was observed between the donors with the lowest and highest CYP3A activity. The between-day variability in testosterone 6β-hydroxylation activity determinations was low, ranging from 2 to 14%.

The individual intrinsic clearance values determined in the current study showed a more than 800-fold difference, ranging from 17.0 to 14,000 μl · min−1 · mg−1 for atorvastatin and saquinavir, respectively (Fig. 2). HJM 1 showed the lowest CYP3A activity and resulted, on average, in the lowest intrinsic clearance values for the drugs investigated. In contrast, HJM 6 generally resulted in the highest clearance values while displaying the second highest CYP3A activity. The mean HJM intrinsic clearance values ranged from 33.5 to 7220 μl · min−1 · mg−1 for atorvastatin and saquinavir, respectively, whereas the coefficient of variation ranged from 41 to 67% for simvastatin and tacrolimus, respectively (Table 4). Overall, the testosterone 6β-hydroxylation activity was a reasonable predictor for intrinsic clearance values between different individual jejunal microsomal preparations (R2 = 0.72 combined data of all 12 substrates). The intrinsic clearance values of atorvastatin and saquinavir were poorly correlated with testosterone 6β-hydroxylation activity (R2 < 0.30), in contrast to the good correlation seen for buspirone, midazolam and simvastatin (R2 > 0.85).

Fig. 2.
Fig. 2.

Individual unbound intrinsic clearance values from eight HJM preparations for atorvastatin (ATV), buspirone (BSP), cyclosporine (CYS), felodipine (FDP), indinavir (IDV), lovastatin (LVS), midazolam (MDZ), nisoldipine (NSP), saquinavir (SQV), simvastatin (SVS), tacrolimus (TCL), and terfenadine (TFD); HJM 1 (▵), HJM 2 (□), HJM 3 (▿), HJM 4 (○), HJM 5 (Embedded Image), HJM 6 (▩), HJM 7 (Embedded Image), and HJM 8 (Embedded Image); for tacrolimus, CLuint data in HJM preparation 7 were not included, as the no-NADP incubation showed extensive drug depletion.

View this table:
TABLE 4

Individual CLuint values of 12 drugs determined by a substrate depletion method in eight individual HJM preparations and comparison to previously published data in human intestinal and hepatic microsomal pools

To assess the Km values of indinavir, felodipine, nisoldipine, and saquinavir, intrinsic clearance values were measured via a substrate depletion approach across a range of substrate concentrations. The Km values were estimated using eq. 2 at 0.1 ± 0.01 (mean and SE from the fit), 0.3 ± 0.02, 2.1 ± 0.3, and 5.3 ± 0.4 μM for indinavir, saquinavir, nisoldipine, and felodipine, respectively.

Mechanistic Predictions of FG and Comparison to the QGut Model.

The predictions of intestinal first-pass metabolism were based on the PBPK model outlined under Materials and Methods. Differential CYP3A amounts along the small intestine, intestinal transit time, drug-specific absorption rates, and differential blood flows to the intestinal segments were taken into account. Furthermore, the inclusion of Michaelis-Menten kinetic parameters allowed the assessment of potential nonlinear first-pass metabolism in small intestine and liver.

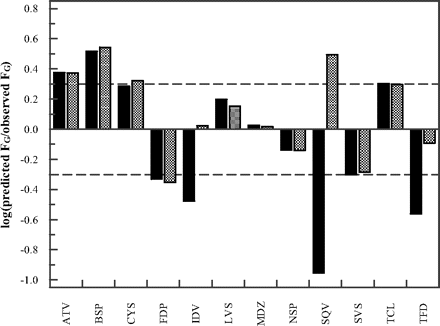
The FG predictions obtained by the PBPK model were compared with the predictions obtained by the QGut model (Fig. 3). To allow a direct comparison between the models, our previously published in vitro intrinsic clearance and permeability data were used (Table 5). The FG predictions of atorvastatin, felodipine, midazolam, nisoldipine, and simvastatin were marginally affected by the choice of model. However, considerable differences were observed in the FG predictions of indinavir, saquinavir, and terfenadine for which the PBPK model predicted higher FG values, more in line with the observed data. The FG predictions for indinavir, saquinavir, and terfenadine using the PBPK model were 0.98, 0.56, and 0.32, respectively. Differences in the FG estimates were due to the ability of the PBPK model to account for saturation of intestinal metabolism by using Vmax and Km data rather than CLint. In contrast to indinavir, the predicted FG values of saquinavir and terfenadine were very sensitive to changes in the Km values used. A reduction in prediction accuracy was observed for buspirone and cyclosporine when the PBPK model was compared with the QGut model. For these drugs, FG overprediction observed using the QGut model increased further in the PBPK model (e.g., for cyclosporine from 93 to 110% overprediction). For tacrolimus, a reduction in enterocytic blood flow in response to a reduction in cardiac output with age resulted in lower FG estimates than those reported previously (clinical data of tacrolimus were generally reported in individuals aged 50 or older). This result was accurately accounted for by both models. An overall improvement in FG predictions was observed using the PBPK model as measured by the decrease in geometric mean fold error (from 2.4 to 1.8) and root mean squared error value (from 0.32 to 0.28) in comparison with those for the QGut model.

Fig. 3.
Fig. 3.

Drug-specific FG prediction success using the QGut (Gertz et al., 2010) or the PBPK model (■ and ▩, respectively) of atorvastatin (ATV), buspirone (BSP), cyclosporine (CYS), felodipine (FDP), indinavir (IDV), lovastatin (LVS), midazolam (MDZ), nisoldipine (NSP), saquinavir (SQV), simvastatin (SVS), tacrolimus (TCL), and terfenadine (TFD); dashed lines indicate a 2-fold deviation from unity. In vitro clearance and permeability data used are listed in Table 2.

View this table:
TABLE 5

Comparison of predicted FG and apparent intravenous and oral clearance data for 12 drugs and observed data

Predictions were performed using either the QGut or PBPK modeling approach.

Prediction of Apparent Oral Clearance.

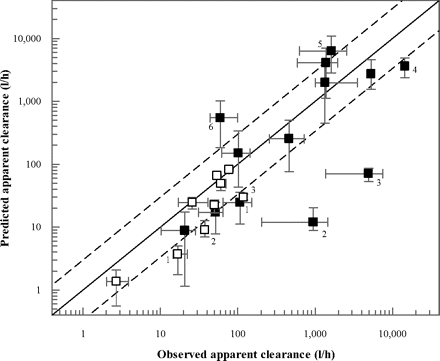
In contrast with the QGut model, the PBPK model also allowed the prediction of apparent oral clearance data of the 12 drugs investigated. Analogous to the FG predictions, this analysis was performed using the mean in vitro intrinsic clearance data from the HIM and HLM pools summarized in Table 4. The predicted oral clearance values are summarized in Table 5 and Fig. 4. The in vivo oral clearance data ranged from 20.7 to 14,400 l/h for tacrolimus and saquinavir, respectively; for cyclosporine and tacrolimus, observed oral clearance values were obtained from blood data. Prediction success of apparent oral clearance inside 3-fold of unity was observed for cyclosporine (Neoral), felodipine, lovastatin, midazolam, nisoldipine, tacrolimus, and terfenadine. For cyclosporine, indinavir, saquinavir, and terfenadine, incomplete absorption was predicted using the drug solubility data (Table 5).

Fig. 4.
Fig. 4.

Comparison of observed and predicted apparent clearance after intravenous (□) and oral (■) administration. In all instances data represent plasma clearance, with the exception of cyclosporine and tacrolimus (blood clearance). Predictions were performed using the in vitro data (Table 2) and the current PBPK model. The clinical data were determined by meta-analyses (Gertz et al., 2010); the error bars on the x- and y-axis indicate the range in the clinical data and in the predictions using different microsomal pools, respectively. The dashed lines indicate a 3-fold deviation from unity; outliers are highlighted: 1, cyclosporine; 2, atorvastatin; 3, buspirone; 4, saquinavir; 5, simvastatin; and 6, indinavir.

Due to a combination of underprediction of hepatic and intestinal clearance, a particularly low prediction success of oral clearance was observed for atorvastatin and buspirone (both <2% of the observed value). In contrast, overpredictions of oral clearance were observed for indinavir and simvastatin. These were due to an approximately 2-fold overprediction of hepatic intrinsic clearance (Table 2) for both drugs. In addition, for indinavir, the incorporation of drug solubility data predicted incomplete absorption (61%), which contributed to the overprediction of CLoral. Saturation of hepatic first-pass metabolism of indinavir, on the other hand, was predicted by the model, as illustrated by the ratio of the areas under the curve in hepatic out- and inlet (FH = 32 versus 11% under linear conditions). For felodipine, overprediction of intestinal metabolism (observed and predicted FG values were 0.45 and 0.20, respectively) and underprediction of apparent hepatic clearance (Table 5) resulted in underprediction of apparent CLoral by 1.8-fold. Overall, the average bias was 4.7-fold for the predictions of apparent oral clearance, largely driven by the extensive underpredictions for buspirone and atorvastatin CLoral; removal of these two drugs from the dataset reduced the bias to 2.9-fold.

Predictions of FG Values from Individual Human Jejunal Microsomes.

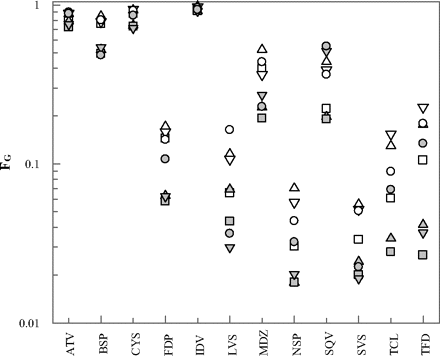
FG predictions were also performed using individual data from eight human jejunal microsomal preparations (Fig. 5). In accordance with the generally higher in vitro clearance data obtained in the individual HJM in comparison to the HIM pool (Table 4), the predicted FG values were overall lower than those obtained from data in pooled microsomes. Mean FG predictions ranged from 0.03 to 0.94 for simvastatin and indinavir, respectively (Table 6). The coefficient of variation in FG predictions from the individual HJM clearance data ranged from 3 to 65% for indinavir and terfenadine, respectively. The FG predictions of terfenadine showed the highest CV of all drugs investigated, resulting in an 8.5-fold difference between the lowest and highest estimate. The remaining drugs showed less than 5-fold differences with the exception of lovastatin and tacrolimus (both 5.5-fold). The lowest FG values (∼2%) were predicted for nisoldipine from HJM preparations 5, 6, and 7, which also showed the highest intrinsic clearance values of nisoldipine (Figs. 2 and 5). Higher CLuint values were determined for saquinavir; however, these did not result in lower FG values because of the prediction of saturation of intestinal first-pass for this drug. The highest FG values and lowest CV were predicted for indinavir (0.92–0.98). This result was not due to low metabolic clearance, the average CLuint value of indinavir being 645 μl · min−1 · mg−1 (greater than midazolam intrinsic clearance) but was due to the prediction of extensive saturation of intestinal metabolism. Consistent with the predictions based on the data from microsomal pools, considerable FG overpredictions were apparent for atorvastatin and buspirone from the individual microsomal preparations (2–3-fold, respectively).

Fig. 5.
Fig. 5.

Individual FG predictions using the mechanistic first-pass model and intrinsic clearance data determined in eight individual HJM preparations (Fig. 2) for atorvastatin (ATV), buspirone (BSP), cyclosporine (CYS), felodipine (FDP), indinavir (IDV), lovastatin (LVS), midazolam (MDZ), nisoldipine (NSP), saquinavir (SQV), simvastatin (SVS), tacrolimus (TCL), and terfenadine (TFD): HJM 1 (▵), HJM 2 (□), HJM3 (▿), HJM 4 (○), HJM 5 (Embedded Image), HJM 6 (▩), HJM 7 (Embedded Image), and HJM 8 (Embedded Image).

View this table:
TABLE 6

Summary of the average, range, and CV of FG values predicted from individual clearance data determined in eight human jejunal microsomal preparations using the PBPK modeling approach

Intrinsic clearance data from eight individual HJM were used to assess interindividual variation of FG. In the literature, very few clinical studies report individual data to allow an estimation of interindividual variability of this parameter. For felodipine, individual area under the curve data before and after grapefruit juice coadministration have been reported in four separate studies, for a total of 45 individuals, summarized in Gertz et al. (2008a). The mean FG of felodipine was 0.45; this estimate was associated with a between-individual variability of 41% and ranged from 0.12 to 1.0 (8.3-fold between highest and lowest FG). By using the HJM clearance data, the predicted FG of felodipine was 0.11 (range 0.06–0.17), and the CV of 42% reflected the variability observed in vivo. In the case of midazolam, individual data after intravenous and oral dose have been reported in 20 individuals (Thummel et al., 1996). This study indicated a 41% interindividual variability of FG, which ranged from 0.21 to 0.94 (4.6-fold ratio between highest and lowest FG). By using the HJM clearance data, the predicted FG of midazolam was 0.33 (range 0.19–0.52) with a CV of 36%, which reflected the variability observed in vivo.

Discussion

Determination of Intestinal Clearance In Vitro.

The in vitro clearance values from eight individual human jejunal microsomal samples compared well with our previous data generated in pooled human intestinal microsomes (Table 4). The CYP3A activity was considerably greater than that in the HIM pool, despite the fact that elution methods were used in both cases to obtain the microsomes (1.84 and 4.12 nmol · min−1 · mg−1 for HIM pool and HJM, respectively). The mean activity of the HJM was comparable to the mean of the three HLM pools (4.65 nmol · min−1 · mg−1). The between-individual variability of 36% was lower than anticipated from reports on tacrolimus and cyclosporine in 14 small intestinal samples, for which the between-subject variability was 54 to 70%, a 4.6- to 11-fold difference between highest and lowest activity in contrast to 2.8-fold in the current study (Lampen et al., 1995, 1996). Considering the relatively small sample size, one can question whether the current HJM selection accurately reflects the true population variability of intestinal CYP3A activity. However, to our knowledge this is the largest dataset of intrinsic clearance data obtained in individual intestinal microsomes in the current literature.

Prediction of FG Using PBPK Modeling.

In this study, a PBPK model was applied to make predictions of intestinal availability using in vitro clearance and permeability data for 12 selected drugs. The analysis focused on drugs with high intestinal extraction in vivo, because FG prediction accuracy for these drugs based on the QGut model was lower that for drugs with FG >0.5 (Gertz et al., 2010). Use of the PBPK model improved FG prediction, resulting in lower bias and increased precision. In contrast to the QGut model, the PBPK model accounted for substrate concentrations at the enzyme site, Michaelis-Menten constants, and potential saturation of metabolism. In addition, the PBPK model accommodated any potential regional differences in intestinal availability because of the heterogeneous expression of CYP3A enzymes along the small intestine (Paine et al., 1997). Solubility of cyclosporine, indinavir, saquinavir, and terfenadine in simulated small intestinal fluids under fasted conditions was taken into account; for cyclosporine, these data compared well with reports in actual human intestinal fluids (Table 3). Because of a lack of transporter-specific kinetic data (Km and Vmax and regional abundance data for key transporters in the small intestine), the current model did not account for active uptake or efflux in either the small intestine or the liver, which may contribute to the absorption and disposition of a number of drugs in the current dataset. At present, even for P-glycoprotein, the most studied transporter in the small intestine, conflicting reports regarding its distribution exist in the literature. Data are generally based on either mRNA levels (Nakamura et al., 2002; Thörn et al., 2005; Berggren et al., 2007), or, if protein levels are determined, on a small sample size (n = 4) (Mouly and Paine, 2003) or on comparison of regional preparations from different individuals (Berggren et al., 2007). We refrained from performing a sensitivity analysis on the interplay of CYP3A and P-glycoprotein, as a publication dedicated exclusively to that effect has been presented (Darwich et al., 2011).

In addition to the need for more informative data on intestinal transporters, refinement of regional cytochrome P450 contents based on a larger number of individuals and preferably determined by a less destructive preparation technique will provide greater confidence in the predictions of intestinal metabolism. The current data presented by Paine et al. (1997) are based on a mucosal scraping technique and a relatively small sample size, in contrast to hepatic CYP3A content data obtained from a meta-analysis of a large number of individuals (Rostami-Hodjegan and Tucker, 2007).

Prediction of Apparent Intravenous and Oral Clearance.

Successful predictions of apparent oral clearance (inside 3-fold) were obtained using pooled microsomal intrinsic clearance data for 6 of 12 drugs. In contrast, large underpredictions of oral clearance were observed for atorvastatin and buspirone (consistent with underprediction of CLi.v.). The metabolism of buspirone has been suggested to be mainly mediated by CYP3A and a similar metabolite pattern in HLM was reported in comparison with that in vivo (Jajoo et al., 1989; Zhu et al., 2005). Previously reported metabolite formation data resulted in marginally higher CLuint values (correction for fuinc applied) compared with our substrate depletion data (460 versus 268 μl · min−1 · mg−1) (Zhu et al., 2005; Gertz et al., 2010). Buspirone clinical data after intravenous administration in eight volunteers were highly variable (i.e., CLp = 28.3 ± 10.3 ml · min−1 · mg−1, F = 3.9 ± 4.3%) with negligible renal excretion of unchanged drug (Gammans et al., 1986). However, neither the variability in the in vivo data nor the differences in the in vitro data are sufficient to explain the extensive underprediction of intrinsic hepatic clearance, because the in vitro data would classify buspirone as a low to moderate extraction drug (EH = 38%; Table 5), whereas the in vivo data show clearance values in excess of hepatic blood flow.

A number of factors may contribute to the extensive underprediction of both intravenous and oral clearance of atorvastatin. First, in vitro data have highlighted drug affinity for uptake transporters (Kameyama et al., 2005) and studies in polymorphic organic anion-transporting polypeptide 1B1 populations confirmed the clinical relevance of at least organic anion-transporting polypeptide 1B1 to atorvastatin disposition (Pasanen et al., 2007). It has been suggested that interconversion between acid and lactone forms may represent the initial step in atorvastatin metabolism (Jacobsen et al., 2000); this may occur directly from the parent or from the acyl glucuronide metabolite (Prueksaritanont et al., 2002). In human liver microsomes, the lactone displays on average a 70-fold greater intrinsic clearance than the hydroxy acid form (Jacobsen et al., 2000). Incorporation of the higher intrinsic clearance of the lactone form into the current analysis resulted in apparent intravenous and oral clearance values of 54.4 and 786 l/h, respectively, and better agreement with the observed data (37.5 and 949 l/h, respectively). The acid-lactone conversion was assumed to occur in plasma and therefore only CLuint for hepatic metabolism was modified in the PBPK model, whereas intestinal intrinsic clearance remained unaltered. However, given the large variability in the ratio of CLint of the lactone and the acid form (14- to 160-fold reported from four individual HLM) (Jacobsen et al., 2000), more data are required to investigate the rate-limiting step in atorvastatin metabolism.

In the case of cyclosporine, the reason for an ∼5-fold underprediction of intrinsic clearance is unclear. Although UDP-glucuronosyltransferase-mediated metabolism in HLM has been reported (Strassburg et al., 2001), we were unable to confirm this by a substrate depletion assay performed in alamethicin-activated microsomes in the absence and presence of bovine serum albumin (data not shown). The underestimation of CLint, h of cyclosporine was masked in the reasonably well predicted oral clearance by the fact that cyclosporine absorption was also underestimated (Fa of 24 and 16% for Neoral and Sandimmune, respectively).

FG Predictions Using Individual Jejunal Microsomal Samples.

Intrinsic clearance data from eight individual HJM were used to predict FG and associated interindividual variability. Individual in vivo FG values were reported for terfenadine, tacrolimus, midazolam, and felodipine in 6, 12, 20, and 45 individuals, respectively. Use of individual HJM clearance data in the PBPK model resulted in an underprediction of felodipine FG (consistent with the pooled data); however, the predicted variability in FG reflected the variability seen in vivo. Considering extensive binding of felodipine to plasma proteins (>99%) (Table 2), binding to enterocytic proteins during absorption cannot be ruled out. Any binding to the enterocytic proteins would lead to reduced apparent intestinal clearance and therefore increased FG predictions. Midazolam FG was well predicted using the pooled microsomal CLuint data but underpredicted using the individual HJM data. Although the coefficient of variation was predicted reasonably well, the FG range was underpredicted. In particular, the ability to predict the upper limit of in vivo FG values was poor, suggesting that selected individual jejunal donors did not cover the full spectrum of CYP3A activity present in the small intestine in vivo.

Other examples for which individual estimates of FG were available in the literature include tacrolimus (Floren et al., 1997; Hebert et al., 1999) and terfenadine (Clifford et al., 1997). The interindividual variabilities of in vivo FG estimates for tacrolimus and terfenadine were 36 and 54%, respectively. Both the CV and the fold difference between the highest and lowest FG values were overpredicted for terfenadine. In addition, the mean predicted FG of terfenadine was underestimated using the individual HJM data. Extensive binding to microsomal proteins has been observed for terfenadine using equilibrium dialysis (Gertz et al., 2008b). Any inaccuracies in the fuinc estimate will bias the estimate of intrinsic clearance and also the estimate of unbound Km used in the PBPK model. In contrast, prediction of the mean tacrolimus FG was more successful (0.08 versus 0.14 for the predicted and observed FG, respectively); however, both the CV and the fold difference were overpredicted using the intrinsic clearance data from eight individual HJM (CV = 58% and 5.5-fold). As an alternative, a propagation of the variability in CYP3A in the small intestine (von Richter et al., 2004) using Monte Carlo simulations may be used to predict interindividual variability of intestinal metabolism and FG. However, it has to be emphasized that CYP3A abundance of a larger population needs to be assessed to capture the interindividual variability correctly.

In conclusion, the use of a PBPK model to study intestinal metabolism represents an improvement over the previously reported FG predictions of high-extraction drugs using the QGut model. Accounting for drug concentration and the region of absorption plays an important role in the assessment of intestinal metabolism and can be propagated into assessment of potential drug-drug interactions. In addition to FG predictions, the PBPK model allowed the assessment of apparent intravenous and oral clearance, with the majority of the drugs predicted within 3-fold of the observed data. Finally, the contribution of intestinal transporters or metabolizing enzymes other than CYP3A needs to be integrated in the models; currently, this is limited by the general lack of unambiguous abundance data in tandem with drug-specific in vitro kinetic data.

Authorship Contributions

Participated in research design: Galetin, Gertz, and Houston.

Conducted experiments: Gertz.

Performed data analysis: Gertz.

Wrote or contributed to the writing of the manuscript: Gertz, Galetin, and Houston.

Other: Galetin and Houston.

Acknowledgments

We thank Sue Murby for technical assistance with LC-MS/MS analyses and Professor Leon Aarons and Drs. Kayode Ogungbenro and Henry Pertinez for useful discussions on the PBPK model (all University of Manchester, Manchester, UK). Additional thanks go to Suet Mei Wong at Pfizer, Pharmacokinetics, Dynamics and Metabolism group (Sandwich, UK) for the determination of solubility data in fasted simulated small intestinal fluids.

Footnotes

  • This work was supported by a consortium of pharmaceutical companies (GlaxoSmithKline, Lilly, Novartis, Pfizer, and Servier) within the Centre for Applied Pharmacokinetic Research at the University of Manchester.

  • Article, publication date, and citation information can be found at http://dmd.aspetjournals.org.

    doi:10.1124/dmd.111.039248.

  • ↵Embedded Image The online version of this article (available at http://dmd.aspetjournals.org) contains supplemental material.

  • ABBREVIATIONS:

    FG
    intestinal availability
    QGut
    hybrid parameter of enterocytic blood flow and drug permeability
    PBPK
    physiologically based pharmacokinetic
    HJM
    human jejunal microsomes
    LC
    liquid chromatography
    MS/MS
    tandem mass spectrometry
    MDCK-MDR1
    Madin-Darby canine kidney cells transfected with human MDR1 gene
    CL
    clearance
    fu
    fraction unbound
    HIM
    human intestinal microsomes
    HLM
    human liver microsomes
    CV
    coefficient of variation.

  • Received March 2, 2011.
  • Accepted June 1, 2011.

References

  1. ↵
    1. Agoram B,
    2. Woltosz WS,
    3. Bolger MB
    (2001) Predicting the impact of physiological and biochemical processes on oral drug bioavailability. Adv Drug Deliv Rev 50 (Suppl 1):S41–S67.
    OpenUrlCrossRefPubMed
  2. ↵
    1. Berggren S,
    2. Gall C,
    3. Wollnitz N,
    4. Ekelund M,
    5. Karlbom U,
    6. Hoogstraate J,
    7. Schrenk D,
    8. Lennernäs H
    (2007) Gene and protein expression of P-glycoprotein, MRP1, MRP2, and CYP3A4 in the small and large human intestine. Mol Pharm 4:252–257.
    OpenUrlCrossRefPubMed
  3. ↵
    1. Brown RP,
    2. Delp MD,
    3. Lindstedt SL,
    4. Rhomberg LR,
    5. Beliles RP
    (1997) Physiological parameter values for physiologically based pharmacokinetic models. Toxicol Ind Health 13:407–484.
    OpenUrlFREE Full Text
  4. ↵
    1. Chalasani N,
    2. Gorski JC,
    3. Patel NH,
    4. Hall SD,
    5. Galinsky RE
    (2002) Reply to Rostami-Hodjegan and Tucker 2002; Hepatology 35(5): 1549–1550. Hepatology 35:1550–1551.
    OpenUrlCrossRef
  5. ↵
    1. Clifford CP,
    2. Adams DA,
    3. Murray S,
    4. Taylor GW,
    5. Wilkins MR,
    6. Boobis AR,
    7. Davies DS
    (1997) The cardiac effects of terfenadine after inhibition of its metabolism by grapefruit juice. Eur J Clin Pharmacol 52:311–315.
    OpenUrlCrossRefPubMed
  6. ↵
    1. Darwich AS,
    2. Neuhoff S,
    3. Jamei M,
    4. Rostami-Hodjegan A
    (2011) Interplay of metabolism and transport in determining oral drug absorption and gut wall metabolism: a simulation assessment using the “Advanced Dissolution, Absorption, Metabolism (ADAM)” model. Curr Drug Metab 11:716–729.
    OpenUrl
  7. ↵
    1. Floren LC,
    2. Bekersky I,
    3. Benet LZ,
    4. Mekki Q,
    5. Dressler D,
    6. Lee JW,
    7. Roberts JP,
    8. Hebert MF
    (1997) Tacrolimus oral bioavailability doubles with coadministration of ketoconazole. Clin Pharmacol Ther 62:41–49.
    OpenUrlCrossRefPubMed
  8. ↵
    1. Galetin A,
    2. Gertz M,
    3. Houston JB
    (2008) Potential role of intestinal first-pass metabolism in the prediction of drug-drug interactions. Expert Opin Drug Metab Toxicol 4:909–922.
    OpenUrlCrossRefPubMed
  9. ↵
    1. Gammans RE,
    2. Mayol RF,
    3. LaBudde JA
    (1986) Metabolism and disposition of buspirone. Am J Med 80 (3B):41–51.
    OpenUrlPubMed
  10. ↵
    1. Gertz M,
    2. Davis JD,
    3. Harrison A,
    4. Houston JB,
    5. Galetin A
    (2008a) Grapefruit juice-drug interaction studies as a method to assess the extent of intestinal availability: utility and limitations. Curr Drug Metab 9:785–795.
    OpenUrlCrossRefPubMed
  11. ↵
    1. Gertz M,
    2. Harrison A,
    3. Houston JB,
    4. Galetin A
    (2010) Prediction of human intestinal first-pass metabolism of 25 CYP3A substrates from in vitro clearance and permeability data. Drug Metab Dispos 38:1147–1158.
    OpenUrlAbstract/FREE Full Text
  12. ↵
    1. Gertz M,
    2. Kilford PJ,
    3. Houston JB,
    4. Galetin A
    (2008b) Drug lipophilicity and microsomal protein concentration as determinants in the prediction of the fraction unbound in microsomal incubations. Drug Metab Dispos 36:535–542.
    OpenUrlAbstract/FREE Full Text
  13. ↵
    1. Granger DN,
    2. Richardson PD,
    3. Kvietys PR,
    4. Mortillaro NA
    (1980) Intestinal blood flow. Gastroenterology 78:837–863.
    OpenUrlPubMed
  14. ↵
    1. Hebert MF,
    2. Fisher RM,
    3. Marsh CL,
    4. Dressler D,
    5. Bekersky I
    (1999) Effects of rifampin on tacrolimus pharmacokinetics in healthy volunteers. J Clin Pharmacol 39:91–96.
    OpenUrlCrossRefPubMed
  15. ↵
    1. Hintz RJ,
    2. Johnson KC
    (1989) The effect of particle size distribution on dissolution rate and oral absorption. Int J Pharm 51:9–17.
    OpenUrlCrossRef
  16. ↵
    1. Valetin J
    International Commission on Radiological Protection (2002) ICRP Publication 89: Basic Anatomical and Physiological Data for Use in Radiological Protection: Reference Values (Valetin J ed), Pergamon, Oxford, UK.
  17. ↵
    1. Jacobsen W,
    2. Kuhn B,
    3. Soldner A,
    4. Kirchner G,
    5. Sewing KF,
    6. Kollman PA,
    7. Benet LZ,
    8. Christians U
    (2000) Lactonization is the critical first step in the disposition of the 3-hydroxy-3-methylglutaryl-CoA reductase inhibitor atorvastatin. Drug Metab Dispos 28:1369–1378.
    OpenUrlAbstract/FREE Full Text
  18. ↵
    1. Jajoo HK,
    2. Mayol RF,
    3. LaBudde JA,
    4. Blair IA
    (1989) Metabolism of the antianxiety drug buspirone in human subjects. Drug Metab Dispos 17:634–640.
    OpenUrlAbstract
  19. ↵
    1. Jamei M,
    2. Turner D,
    3. Yang J,
    4. Neuhoff S,
    5. Polak S,
    6. Rostami-Hodjegan A,
    7. Tucker G
    (2009) Population-based mechanistic prediction of oral drug absorption. AAPS J 11:225–237.
    OpenUrlCrossRefPubMed
  20. ↵
    1. Kameyama Y,
    2. Yamashita K,
    3. Kobayashi K,
    4. Hosokawa M,
    5. Chiba K
    (2005) Functional characterization of SLCO1B1 (OATP-C) variants, SLCO1B1*5, SLCO1B1*15 and SLCO1B1*15+C1007G, by using transient expression systems of HeLa and HEK293 cells. Pharmacogenet Genomics 15:513–522.
    OpenUrlCrossRefPubMed
  21. ↵
    1. Kolars JC,
    2. Lown KS,
    3. Schmiedlin-Ren P,
    4. Ghosh M,
    5. Fang C,
    6. Wrighton SA,
    7. Merion RM,
    8. Watkins PB
    (1994) CYP3A gene expression in human gut epithelium. Pharmacogenetics 4:247–259.
    OpenUrlCrossRefPubMed
  22. ↵
    1. Lampen A,
    2. Christians U,
    3. Bader A,
    4. Hackbarth I,
    5. Sewing KF
    (1996) Drug interactions and interindividual variability of ciclosporin metabolism in the small intestine. Pharmacology 52:159–168.
    OpenUrlPubMed
  23. ↵
    1. Lampen A,
    2. Christians U,
    3. Guengerich FP,
    4. Watkins PB,
    5. Kolars JC,
    6. Bader A,
    7. Gonschior AK,
    8. Dralle H,
    9. Hackbarth I,
    10. Sewing KF
    (1995) Metabolism of the immunosuppressant tacrolimus in the small intestine: cytochrome P450, drug interactions, and interindividual variability. Drug Metab Dispos 23:1315–1324.
    OpenUrlAbstract
  24. ↵
    1. Lennernäs H
    (2003) Clinical pharmacokinetics of atorvastatin. Clin Pharmacokinet 42:1141–1160.
    OpenUrlCrossRefPubMed
  25. ↵
    1. Mouly S,
    2. Paine MF
    (2003) P-glycoprotein increases from proximal to distal regions of human small intestine. Pharm Res 20:1595–1599.
    OpenUrlCrossRefPubMed
  26. ↵
    1. Nakamura T,
    2. Sakaeda T,
    3. Ohmoto N,
    4. Tamura T,
    5. Aoyama N,
    6. Shirakawa T,
    7. Kamigaki T,
    8. Nakamura T,
    9. Kim KI,
    10. Kim SR,
    11. et al
    . (2002) Real-time quantitative polymerase chain reaction for MDR1, MRP1, MRP2, and CYP3A-mRNA levels in Caco-2 cell lines, human duodenal enterocytes, normal colorectal tissues, and colorectal adenocarcinomas Drug Metab Dispos 30:4–6.
    OpenUrlAbstract/FREE Full Text
  27. ↵
    1. Nestorov I
    (2003) Whole body pharmacokinetic models. Clin Pharmacokinet 42:883–908.
    OpenUrlCrossRefPubMed
  28. ↵
    1. Obach RS,
    2. Reed-Hagen AE
    (2002) Measurement of Michaelis constants for cytochrome P450-mediated biotransformation reactions using a substrate depletion approach. Drug Metab Dispos 30:831–837.
    OpenUrlAbstract/FREE Full Text
  29. ↵
    1. Paine MF,
    2. Hart HL,
    3. Ludington SS,
    4. Haining RL,
    5. Rettie AE,
    6. Zeldin DC
    (2006) The human intestinal cytochrome P450 “pie.” Drug Metab Dispos 34:880–886.
    OpenUrlAbstract/FREE Full Text
  30. ↵
    1. Paine MF,
    2. Khalighi M,
    3. Fisher JM,
    4. Shen DD,
    5. Kunze KL,
    6. Marsh CL,
    7. Perkins JD,
    8. Thummel KE
    (1997) Characterization of interintestinal and intraintestinal variations in human CYP3A-dependent metabolism. J Pharmacol Exp Ther 283:1552–1562.
    OpenUrlAbstract/FREE Full Text
  31. ↵
    1. Pasanen MK,
    2. Fredrikson H,
    3. Neuvonen PJ,
    4. Niemi M
    (2007) Different effects of SLCO1B1 polymorphism on the pharmacokinetics of atorvastatin and rosuvastatin. Clin Pharmacol Ther 82:726–733.
    OpenUrlCrossRefPubMed
  32. ↵
    1. Poulin P,
    2. Theil FP
    (2002) Prediction of pharmacokinetics prior to in vivo studies. 1. Mechanism-based prediction of volume of distribution. J Pharm Sci 91:129–156.
    OpenUrlCrossRefPubMed
  33. ↵
    1. Prueksaritanont T,
    2. Subramanian R,
    3. Fang X,
    4. Ma B,
    5. Qiu Y,
    6. Lin JH,
    7. Pearson PG,
    8. Baillie TA
    (2002) Glucuronidation of statins in animals and humans: a novel mechanism of statin lactonization. Drug Metab Dispos 30:505–512.
    OpenUrlAbstract/FREE Full Text
  34. ↵
    1. Rodgers T,
    2. Leahy D,
    3. Rowland M
    (2005) Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J Pharm Sci 94:1259–1276.
    OpenUrlCrossRefPubMed
  35. ↵
    1. Rodgers T,
    2. Rowland M
    (2006) Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci 95:1238–1257.
    OpenUrlCrossRefPubMed
  36. ↵
    1. Rostami-Hodjegan A,
    2. Tucker GT
    (2002) The effects of portal shunts on intestinal cytochrome P450 3A activity. Hepatology 35:1549–1550; author reply 1550–1551.
    OpenUrlCrossRefPubMed
  37. ↵
    1. Rostami-Hodjegan A,
    2. Tucker GT
    (2007) Simulation and prediction of in vivo drug metabolism in human populations from in vitro data. Nat Rev Drug Discov 6:140–148.
    OpenUrlCrossRefPubMed
  38. ↵
    1. Shen DD,
    2. Kunze KL,
    3. Thummel KE
    (1997) Enzyme-catalyzed processes of first-pass hepatic and intestinal drug extraction. Adv Drug Deliv Rev 27:99–127.
    OpenUrlCrossRefPubMed
  39. ↵
    1. Strassburg CP,
    2. Barut A,
    3. Obermayer-Straub P,
    4. Li Q,
    5. Nguyen N,
    6. Tukey RH,
    7. Manns MP
    (2001) Identification of cyclosporine A and tacrolimus glucuronidation in human liver and the gastrointestinal tract by a differentially expressed UDP-glucuronosyltransferase: UGT2B7. J Hepatol 34:865–872.
    OpenUrlCrossRefPubMed
  40. ↵
    1. Tam D,
    2. Tirona RG,
    3. Pang KS
    (2003) Segmental intestinal transporters and metabolic enzymes on intestinal drug absorption. Drug Metab Dispos 31:373–383.
    OpenUrlAbstract/FREE Full Text
  41. ↵
    1. Thörn M,
    2. Finnström N,
    3. Lundgren S,
    4. Rane A,
    5. Lööf L
    (2005) Cytochromes P450 and MDR1 mRNA expression along the human gastrointestinal tract. Br J Clin Pharmacol 60:54–60.
    OpenUrlCrossRefPubMed
  42. ↵
    1. Thummel KE,
    2. O'Shea D,
    3. Paine MF,
    4. Shen DD,
    5. Kunze KL,
    6. Perkins JD,
    7. Wilkinson GR
    (1996) Oral first-pass elimination of midazolam involves both gastrointestinal and hepatic CYP3A-mediated metabolism. Clin Pharmacol Ther 59:491–502.
    OpenUrlCrossRefPubMed
  43. ↵
    1. von Richter O,
    2. Burk O,
    3. Fromm MF,
    4. Thon KP,
    5. Eichelbaum M,
    6. Kivistö KT
    (2004) Cytochrome P450 3A4 and P-glycoprotein expression in human small intestinal enterocytes and hepatocytes: a comparative analysis in paired tissue specimens. Clin Pharmacol Ther 75:172–183.
    OpenUrlCrossRefPubMed
  44. ↵
    1. Yang J,
    2. Jamei M,
    3. Yeo KR,
    4. Tucker GT,
    5. Rostami-Hodjegan A
    (2007) Prediction of intestinal first-pass drug metabolism. Curr Drug Metab 8:676–684.
    OpenUrlCrossRefPubMed
  45. ↵
    1. Yeh KC,
    2. Stone JA,
    3. Carides AD,
    4. Rolan P,
    5. Woolf E,
    6. Ju WD
    (1999) Simultaneous investigation of indinavir nonlinear pharmacokinetics and bioavailability in healthy volunteers using stable isotope labeling technique: study design and model-independent data analysis. J Pharm Sci 88:568–573.
    OpenUrlCrossRefPubMed
  46. ↵
    1. Yu LX,
    2. Amidon GL
    (1999) A compartmental absorption and transit model for estimating oral drug absorption. Int J Pharm 186:119–125.
    OpenUrlCrossRefPubMed
  47. ↵
    1. Yu LX,
    2. Lipka E,
    3. Crison JR,
    4. Amidon GL
    (1996) Transport approaches to the biopharmaceutical design of oral drug delivery systems: prediction of intestinal absorption. Adv Drug Deliv Rev 19:359–376.
    OpenUrlCrossRefPubMed
  48. ↵
    1. Zhang QY,
    2. Dunbar D,
    3. Ostrowska A,
    4. Zeisloft S,
    5. Yang J,
    6. Kaminsky LS
    (1999) Characterization of human small intestinal cytochromes P-450. Drug Metab Dispos 27:804-809.
    OpenUrlAbstract/FREE Full Text
  49. ↵
    1. Zhu M,
    2. Zhao W,
    3. Jimenez H,
    4. Zhang D,
    5. Yeola S,
    6. Dai R,
    7. Vachharajani N,
    8. Mitroka J
    (2005) Cytochrome P450 3A-mediated metabolism of buspirone in human liver microsomes. Drug Metab Dispos 33:500–507.
    OpenUrlAbstract/FREE Full Text
Back to top

In this issue

Download PDF
Article Alerts
Email Article
Citation Tools

Research ArticleArticle

Physiologically Based Pharmacokinetic Modeling of Intestinal First-Pass Metabolism of CYP3A Substrates with High Intestinal Extraction

Michael Gertz, J. Brian Houston and Aleksandra Galetin
Drug Metabolism and Disposition September 1, 2011, 39 (9) 1633-1642; DOI: https://doi.org/10.1124/dmd.111.039248
Twitter logo Facebook logo Mendeley logo

Jump to section

Advertisement