Abstract
Intricacies in intestinal physiology, drug properties, and food effects should be incorporated into models to predict complex oral drug absorption. A previously published human continuous intestinal absorption model based on the convection-diffusion equation was modified specifically for the male Sprague-Dawley rat in this report. Species-specific physiologic conditions along intestinal length - experimental velocity and pH under fasted and fed conditions, were measured and incorporated into the intestinal absorption model. Concentration-time (C-t) profiles were measured upon a single intravenous and peroral (PO) dose for three drugs: amlodipine (AML), digoxin (DIG), and glyburide (GLY). Absorption profiles were predicted and compared with experimentally collected data under three feeding conditions: 12-hour fasted rats were provided food at two specific times after oral drug dose (1 hour and 2 hours for AML and GLY; 0.5 hours and 1 hour for DIG), or they were provided food for the entire study. Intravenous versus PO C-t profiles suggested absorption even at later times and informed design of appropriate mathematical input functions based on experimental feeding times. With this model, AML, DIG, and GLY oral C-t profiles for all feeding groups were generally well predicted, with exposure overlap coefficients in the range of 0.80–0.97. Efflux transport for DIG and uptake and efflux transport for GLY were included, modeling uptake transporter inhibition in the presence of food. Results indicate that the continuous intestinal rat model incorporates complex physiologic processes and feeding times relative to drug dose into a simple framework to provide accurate prediction of oral absorption.
SIGNIFICANCE STATEMENT A novel rat continuous intestinal model predicts drug absorption with respect to time and intestinal length. Feeding time relative to dose was modeled as a key effect. Experimental fasted/fed intestinal pH and velocity, efflux and uptake transporter expression along intestinal length, and uptake transporter inhibition in the presence of food were modeled. The model uses the pharmacokinetic profiles of three model drugs and provides a novel framework to study food effects on absorption.
Introduction
Most drugs are administered orally due to cost efficacy, noninvasiveness, and increased patient compliance (Alqahtani et al., 2021). However, orally administered drugs are subject to complex biologic processes, and their absorption additionally depends on the physicochemical properties of the dosed drug. Biologic parameters contributing to complex intestinal absorption kinetics include gastrointestinal transit, presence and type of food, pH, and transporter expression. Drug properties such as lipophilicity, pKa, along with permeability, solubility, and formulation are also impactful.
One of the most notable contributors to the difficulty of absorption predictions is the effect of food (Welling, 1977; Higashi et al., 2013; Owens et al., 2021). Food has been known to affect gastric emptying, small intestinal transit, pH, blood flow, and transporter expression and can even act as a mechanical barrier or binder (Ward and Coates, 1987; Klein, 2010; Dou et al., 2018). Food effects may explain the interlaboratory variability seen in pharmacokinetic (PK) profiles for the same drug at the same dose (Li et al., 2012; Jiang et al., 2015). Preclinical PK studies are typically performed in fasted rats to reduce the interanimal variability in concentration-time (C-t) profiles (Melander, 1978; Singh et al., 2011; Small et al., 2015). Animals are usually fasted overnight between 12 and 18 hours, which is often noted (Vermeulen et al., 1997). However, most reports fail to specify when animals were fed after drug administration. Further, although rats show similar intestinal permeability and drug absorption as humans (Cao et al., 2006), the usefulness of rat studies is diminished by differences in species-specific physiologic parameters such as transporters. Further, rat anatomy and physiology are markedly different from human, especially regarding the rat versus human stomach and with the presence (human) versus absence (rats) of a gall bladder (DeSesso and Jacobson, 2001; Vdoviakova et al., 2016).
Prediction of PK parameters utilizes a range of modeling methods including classic compartmental models and physiologically based pharmacokinetic (PBPK) models, where compartments represent specific organs or tissues that are connected by blood flows (Lin and Wong, 2017). Hybrid models include the target organ explicitly, whereas the remainder of the body is modeled as mathematical compartments. The most widely used absorption models in humans are the Advanced Compartmental Absorption and Transit model and the Advanced Dissolution Absorption and Metabolism model, which model the intestine as a series of compartments (Huang et al., 2009). Physiologic factors (pH, gastric emptying, intestinal transit, and transporter expression levels) and physicochemical factors (pKa, particle size, and solubility) are integrated into the model to predict absorption. This model uses ordinary differential equations to predict drug movement in the body. Another approach is to consider the intestine to be a continuous compartment. Absorption is modeled as a change in drug concentration along distance (x) and over time (t) (Nagar et al., 2017). This continuous absorption model was developed based on the convection-diffusion equation (Ni et al., 1980) and is based on partial differential equations (PDEs), which were revisited due to the advancements in computational power and speed. Physiologic parameters are described as functions of x and can vary along the length of the intestine.
The goal of the current work was to develop a mathematical framework for predicting the impact of food and feeding time on oral drug absorption. Our previously published human continuous intestinal model was first modified to create a rat model. The collection of rich physiologic and PK data to develop and refine a rodent model is feasible and provides useful proof-of-concept data, whereas similar data collection may be cost prohibitive or not possible in humans. Rat gastrointestinal anatomy and physiology data were collected and used to build the rat model. Next, three model drugs – amlodipine (AML), digoxin (DIG), and glyburide (GLY) – were dosed intravenously as well as peroral (PO), and concentration-time datasets were collected. The drugs were selected based on differences in their solubility, permeability, and rat transporter profiles. AML is a biopharmaceutics classification system (BCS) class 1 drug and is not a reported transporter substrate in rats. DIG is BCS class 4 and a P-glycoprotein (P-gp) substrate. GLY is BCS class 2 and a P-gp and organic anion transporter protein (Oatp) substrate (El-Kattan and Varma, 2012; Estudante et al., 2013; Suzuki et al., 2014). All datasets were collected at various feeding times postdose. A rat continuous absorption model was developed, and the observed impact of food and feeding time relative to drug dosing on drug absorption was modeled with the absorption model.
Materials and Methods
Chemicals and Reagents
Amlodipine was purchased from Alfa Asear (Haverhill, MA). Glyburide was from Frontier Scientific (Logan, UT). Digoxin was obtained from Tocris (Ellisville, MO). Glyburide-d3 and digoxin-d3 were purchased from Cayman Chemical (Ann Arbor, MI). Amlodipine-d4 was obtained from Toronto Research Chemicals (North York, Canada). Sprague Dawley rat plasma was purchased from Equitech Biotech Inc (Kerrville, TX). Polyethylene glycol 400 (PEG-400) and methylcellulose (viscosity, 400 cP) were from Sigma-Aldrich (St. Louis, MO). 1-Methyl-2-pyrrolidinone (NMP) is from J.T.Baker (Allentown, PA).
Animals
Male Sprague-Dawley single jugular cannulated rats weighing 239–250 g were ordered from Charles River (Wilmington, MA). All rats were singly housed under a reverse 12-hour light/dark cycle. Rats were acclimated for at least four days in the Temple University Health Sciences Campus animal housing facility and 30 minutes in the procedure room prior to the start of the study. Food (standard rodent chow) and water were available ad libitum for fed groups. Food was removed from the cages of fasted groups 12 hours before the beginning of the study. All animal studies were performed with strict adherence to protocols approved by the Temple University IACUC. The total number of animals used was minimized by using the same animal for intestinal measurements after the completion of pharmacokinetic studies.
Rat Intestinal Measurements
Intestinal Dimensions and pH Determination
Rats were euthanized, and their intestines were clamped at the pyloric sphincter and most distal portion of the colon to prevent bodily fluids from entering and influencing pH. The intestines were removed and divided into ten unequal segments. The small intestine was divided into seven segments. The first 10 cm, starting from the pylorus, was labeled the duodenum. The last 3 cm, ending at the cecum, was considered the ileum. The middle portion was divided into five equal parts, with jejunum (J) 1 starting at the end of the duodenum and J5 ending at the start of the ileum. The colon was divided into two equal sections: proximal and distal. The cecum was separately isolated. After pH measurements described below, the intestines were cut along the length to lay flat, taking care not to overstretch the organs. The lengths of the small intestine (n = 43) and colon (n = 14) were measured with a tape measurer and recorded. Each segment’s width (n = 5) was also collected by measuring the distance from one side of the cut to another, perpendicular to the length.
For pH measurement, the luminal contents were removed from each segment by lightly squeezing each segment with a pair of tweezers. A single, similarly-sized fecal pellet in the distal colon was mixed with 0.5 ml of water and vortexed to obtain a homogenous mixture for each rat. No water was added to any other segment. After initial pH measurements, an extra 0.5 mL of water was added to assess the influence of the water on the pH for one rat in each group. The pH of the luminal contents was measured using a precalibrated pH meter between one and three times, remixing between each reading. The order of the segments measured was alternated between animals to minimize postmortem pH drift.
The pH of the food pellets was measured on two separate days to determine the influence of pellet pH on luminal pH. Three standard size rat pellets (∼12 g) were placed in a tube containing 10 mL of water. The pellets were vortexed until entirely disintegrated and no solid pieces could be seen. The pH of the pellet mixture was measured three times, shaking the mixture between measurements.
Gastrointestinal Motility
Rats (n = 36) were divided into one of two condition groups: fasted or fed. Fed (n = 17) and 12-hour fasted (n = 19) male Sprague-Dawley rats were administered 0.5 mL of a 5% activated charcoal in 1.5% methylcellulose by oral gavage.
Rats were euthanized at a predetermined time point of 10, 20, 30, 45, 60, 75, 100, 120, or 180 minutes after dosing. The intestines were removed, divided into the ten segments mentioned previously, and inspected for charcoal visually. The distance traveled by the charcoal plug was measured as the furthest point of the charcoal plug.
Dosing and Sampling of Amlodipine and Glyburide
Rats (n = 3) were intravenously administered a solution containing 2 mg/kg AML and 4 mg/kg GLY prepared in 50%–55% NMP, 20% PEG-400, and 25%–30% Milli-Q water via the jugular cannula. Blood samples (∼0.2 mL) were collected via the jugular cannula into heparinized tubes at 0.08, 0.25, 0.5, 1, 2, 4, 6, 8, 10, and 12 hours postdose. Rats (n = 3) were intravenously administered a solution containing 0.25 mg/kg DIG prepared in 15% NMP with saline via the jugular cannula. Blood samples (∼0.2 mL) were collected via the jugular cannula into heparinized tubes at 0.08, 0.25, 0.5, 0.75, 1, 2, 4, 6, and 8 hours postdose. After each sampling, the loss of blood volume was supplemented with an equal volume of saline containing 100 U/mL heparin. Blood samples were centrifuged at 5000 g for 15 minutes for AML and GLY or 10 000 g for 10 minutes for DIG at 4°C to obtain plasma and kept at −20°C until analysis.
Rats (n = 13) were orally administered a solution containing 5 mg/kg AML and 5 mg/kg GLY in 50%–55% NMP, 20% PEG-400, and 25%–30% Milli-Q water via oral gavage. Although AML is not reported to be a transporter substrate, GLY absorption may be impacted by both uptake and efflux transporters. It is important to note that the use of 20% PEG-400 may alter efflux transporter activity toward GLY (Mudra and Borchardt, 2010), and this caveat was not further explored in the study. Rats were either fed (fed, n = 6), fasted 12 hours and then fed 1-hour postdose [fasted 1 hour feeding time (FT), n = 4], or fasted 12 hours and then fed 2 hours postdose (fasted 2 hours FT, n = 3). Blood samples (∼0.2 mL) were collected via the jugular cannula into heparinized tubes at 0.17, 0.5, 1, 1.5, 2.5, 4, 6, 8, 10, and 24 hours postdose. Blood loss supplementation and plasma sample preparation were the same as that of the AML and GLY intravenous administration study.
Rats (n = 14) were orally administered a solution containing 0.75 mg/kg DIG in 15% NMP in saline via oral gavage. Rats were either fed (fed, n = 5), fasted 12 hours and then fed 0.5 hours postdose (fasted 0.5 hours FT, n = 4), or fasted 12 hours and then fed 1-hour postdose (fasted 1 h FT, n = 5). Blood samples (∼0.2 mL) were collected via the jugular cannula into heparinized tubes at 0.08, 0.25, 0.5, 0.75, 1, 2, 4, 6, 8, and 24 hours postdose. Blood loss supplementation and plasma sample preparation were the same as that of the DIG intravenous administration study.
Plasma samples for AML and GLY were mixed with two and a half times the volume of amlodipine-d4 (25 ng/mL) and glyburide-d3 (150 ng/mL) in acetonitrile as respective internal standards. Samples were vortexed and centrifuged at 15 000 g for 10 minutes at 4°C. Ten microliters supernatant was injected into the liquid chromatography and tandem mass spectrometry (LC-MS/MS) system for analysis. DIG plasma samples were mixed with two times the volume of digoxin-d3 in acetonitrile (ACN). Samples were vortexed and centrifuged at 15 000 g for 10 minutes at 4°C. Twenty microliters supernatant was injected into the LC-MS/MS system for analysis.
Liquid Chromatography Tandem Mass Spectrometry
Analysis was performed using an Agilent series 1100 high-performance liquid chromatography system coupled to an ABSciex API 4000 triple-quadrupole tandem mass spectrometer with an electrospray ionization source. The mass spectrometer was operated in positive ion mode. All LC-MS/MS data were acquired and processed using Analyst software version 1.6.
Chromatographic separation for AML and GLY was performed on a Kinetex C8 column (2.1 mm × 50 mm, 5 µm) protected by a Phenomenex Security Guard C18 (2.0 × 4 mm) guard column. The mobile phase for AML and GLY consisted of water with 0.1% formic acid (FA) as the aqueous phase (A) and ACN with 0.1% FA as the organic phase. The gradient started at 95% A and maintained for 1.3 minutes, ramped down to 0% over 30 seconds and held for 5.7 minutes, and then ramped back to 95% over 10 seconds and maintained until 9 minutes. The flow rate was 500 µL/min. The retention time for AML and AML-d4 was ∼3.00 minutes, whereas the retention time for GLY and GLY-d3 was ∼3.27 minutes. The precursor → product ion transitions observed for AML, AML-d4, GLY, and GLY-d3 were 409.2 → 237.3, 413.2 → 237.3, 494.5 → 369.2, and 497.5 → 372.2, respectively.
For DIG, a Phenomenex Gemini C18 column (100 mm × 4.6 mm, 3 μm) with a Phenomenex Security Guard C18 (2.0 × 4 mm) guard column was used. The mobile phase for DIG consisted of 10 mM ammonium formate in water (pH to 4 with FA) as A and ACN with 0.1% FA as organic phase. The gradient used for DIG elution started at 70% A and maintained for 1 minute, ramped down to 5% over 1.5 minutes and maintained for 2.5 minutes, and increased back to 70% over 0.1 minutes for a total of 7 minutes. The flow rate was 600 μL/min. The retention time for DIG and DIG-d was ∼4.54 minutes. The precursor → product ion transitions analyzed for DIG and DIGd3 were 798.5 → 651.5 and 801.5 → 654.5, respectively.
The dwell time for each ion transition was 200 milliseconds. The operating parameters were optimized as follows: curtain gas, 20 psi; ion source gas 1, 60 psi; ion source gas 2, 40 psi; ion spray voltage, 5000 V; temperature, 500°C. The declustering potential (DP), collision energy (CE), and collision cell exit potential (CXP) for AML are 71V, 17V, and 18V, respectively. The DP, CE, and CXP for GLY are 96V, 21V, and 19V, respectively. The DP, CE, and CXP for DIG are 70V, 20V, and 15V, respectively.
The combined method for AML and GLY was satisfactory for quantification over the range of 1.5–90 ng/mL and 25–1500 ng/mL for AML and GLY in rat plasma, respectively. The method for DIG was suitable for quantification from 0.75–96 ng/mL. The lower limits of quantitation for AML, DIG, and GLY were 1.5 ng/mL, 0.75 ng/mL, and 25 ng/mL, respectively. The inter- and intraday percent accuracy and percent precision were within ± 15% for all three drugs.
Compartmental Modeling of Intravenous Datasets
Individual rat concentration-time profiles as well as naive-pooled averages in each group upon intravenous dosing were used as inputs for compartmental modeling. Assuming linear pharmacokinetics at the doses used, standard compartmental models were used to fit the intravenous datasets. Modeling was conducted with Mathematica version 12.3.1 with 1/y weighting. Model selection was based on corrected Akaike information criterion values, and the compartmental model fitted intravenous concentration-time profiles were used as disposition functions for the absorption model subsequently used for the oral datasets.
Intestinal Model Development
We have previously published in detail a human continuous absorption model (Nagar et al., 2017). The rat model described below used a similar framework, with key anatomic differences modeled as described below. This model predicts the fraction of drug absorbed and can predict bioavailability if first-pass metabolism data are available. The code for this model is provided in Supplemental Materials. The continuous absorption model is based on the basic convection-diffusion equation (Ni et al., 1980):
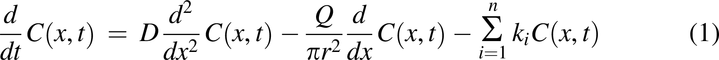
where drug concentration (C) varies as a function of both x and t, D is the drug molecule diffusion coefficient, Q is the bulk fluid flow rate, r is the radius of the intestinal lumen, and ki is the first-order rate constant for the ith radial transfer process. The first term describes axial diffusion, the spread of the drug pulse due to intestinal drug mixing; the second term describes convection, the axial bulk movement of the pulse; and the last term describes radial diffusion. This approach also includes relevant physiological and physicochemical factors.
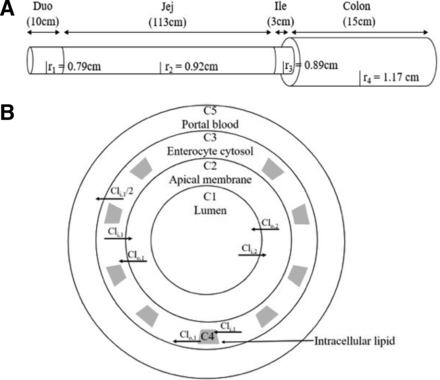
For this model, the intestine is described as a continuous, concentric set of cylinders (Fig. 1). In the axial direction, the drug enters as a plug from the stomach into the duodenum (10 cm), moves along the gut through the jejunum (106 cm), ileum (3 cm), and colon (16 cm) and stops at the terminal colon (Fig. 1A). The model is velocity-based, ensuring that the plug is at the experimentally determined position over time. The small intestine is considered to have a radius of 0.79 cm in the duodenum, 0.92 cm in the jejunum, 0.89 cm in the ileum, and 1.17 cm in the colon.
Rat continuous intestinal absorption model. (A) Depiction of the rat intestine as a continuous cylinder.. (B) Depiction of the radial compartments comprising the concentric cylinders of the rat intestine. Diffusional clearances into (CLi) and out of (CLo) membranes are as defined in Materials and Methods. Duo, duodenum; Jej, jejunum; Ile, ileum; r1, radius of Duo; r2, radius of Jej; r3, radius of Ile; r4, radius of the colon.
In the radial direction, this model includes an explicit enterocyte apical membrane, cytosol, and intercellular lipid compartments (Fig. 1B). For absorption, the drug reversibly moves from the lumen (C1), through the apical enterocyte membrane (C2), and into the enterocyte cytosol (C3), where it has the option to go into intracellular lipids (C4). In the final step, the drug irreversibly moves across the basolateral membrane into the portal blood (C5).
Physiologic Functions
Expressions for relevant physiologic parameters as functions of x were derived using combinations of logistic functions to match experimental data. These functions allowed for smooth transitions between intestinal segments and prevented mathematical discontinuities.
Velocity, vel(x)
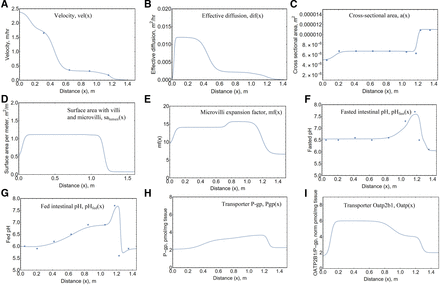
As the bulk pulse travels along the axial direction, it does so with a fluctuating velocity. Experimental time versus position data collected in-house were used to calculate experimental velocities as a function of x. The following expression for vel(x) was built using these velocities. Due to the absorption of luminal water and change in intestinal diameter, the velocity decreases along the small intestine, with the slowest velocity occurring in the colon. Eq. 2 was used, and the profile and experimental velocity data are shown in Fig. 2A.

where a1 is the cross-sectional area at radius r1 and a(x) is the cross-sectional area as a function of x.
Physiologic functions describing the intestine. Functions along x are shown for (A) velocity, vel(x); (B) effective diffusion, dif(x); (C) cross-sectional area, a(x); (D) surface area with villi and microvilli, salumen(x); (E) microvilli expansion factor, mf(x); (F) fasted intestinal pH, pHfast(x); (G) fed intestinal pH, pHfed(x); (H) P-gp pmol/mg tissue, P-gp(x); and (I) Oatb2b1 normalized pmol/mg tissue, Oatp2b1(x). Experimental data when collected in-house are depicted by filled circles.
Effective Diffusion, dif(x)
Along with bulk axial movement, the drug pulse experiences effective axial diffusion. This axial spreading of the plug is greater than that expected by molecular diffusion and is likely due to peristalsis. Similar to the human model (Nagar et al., 2017), effective axial diffusion is a function of velocity, as shown in eq. 3 and Fig. 2B.
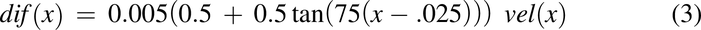
Cross-Sectional Area, a(x)
The cross-sectional area is determined by the radii of each intestinal segment. The radii of the duodenum, jejunum, ileum, and colon are r1, r2, r3, and r4, respectively. Eq. 4 was used, and the profile and experimental velocity data are shown in Fig. 2C:

where a1 = πr12, a2 = πr22, a3 = πr32, a4 = πr42, jej5 = 1.16 m, and ile = 1.19 m were used for distance to the end of the jejunum and ileum, respectively.
Surface Area, sa(x)

The expressions for surface area per unit length (circumference) was based on experimental data collected in-house. The surface areas were determined by the radii and multiplication factors for villi and microvilli. The total surface area including microvilli and villi, salumen(x), is described in eq. 6, and the profile is shown in Fig. 2D. where duo = 0.10 m, jej4 = 0.95 m, jej5 = 1.16 m, and ile = 1.19 m were used for distance to the end of the duodenum, fourth jejunal segment, the entire jejunum, and ileum, respectively.
The expansion factor for the increase in surface area due to microvilli alone, mf(x), is described in eq. 5, and the profile is shown in Fig. 2E.

where duo = 0.10 m, jej3 = 0.74 m, and ile = 1.19 m were used for distance to the end of the duodenum, third jejunal segment, and ileum, respectively. The surface area without microvilli can then be calculated by salumen(x)/mf(x).
Cross-Sectional Area for the Enterocyte Apical Membrane, amem(x); Cytosol, acyt(x); and Cytosolic Lipid, alip(x)
The equations used to describe the cross-sectional area along the intestine for the enterocyte apical membrane, cytosol, and cytosolic lipids are described in more detail previously (Nagar et al., 2017) and are listed below.


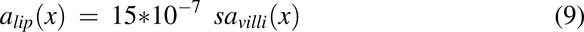
Where savilli(x) equals salumen(x)/mf(x).
pH of the Intestines, pH(x)
Fasted and fed pH data along the intestine was collected experimentally. The pH along the intestine under fasted conditions was described as a combination of logistic functions expressed in eq. 10 and shown in Fig. 2F. The pH along the intestine under fed conditions was described in eq. 11 and shown in Fig. 2G.
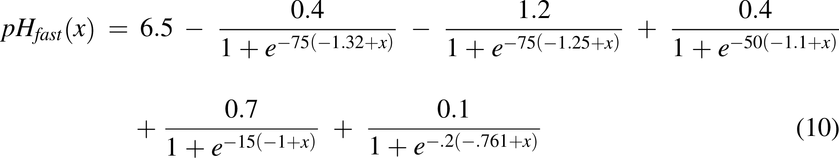

Drug-specific functions:
Apparent Permeability, Papp(x)
For the current model, apparent permeability is based on Caco-2 cell permeability data and is modified by pH as described previously (Nagar et al., 2017). To account for species differences and the transition from in vitro to in vivo, a Caco-2 scaling factor of 1.2 was used. The equations for acids and bases were used were used for Papp(x), respectively.
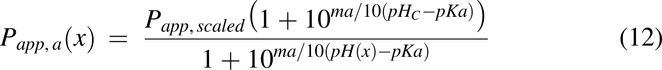
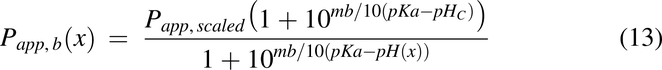
where Papp(x) is the apparent permeability along the intestine, Papp,scaled is the scaled Caco-2 permeability of a specific drug, ma is the slope of permeability versus pH for acids, mb is the slope of permeability versus pH for bases, pHC is the pH at which the Caco-2 experiments were conducted, pKa is the pKa for the drug, and pH(x) is the pH of the intestine at x. The pH(x) used was either pHfast(x) or pHfed(x), depending on the feeding condition of the animals.
Membrane Diffusional Clearances, CLi(x) and CLo(x)
The movement of drug between compartments is described by diffusional clearances CLi(x) and CLo(x). Movement of drug into the membrane is the product of permeability and surface area:
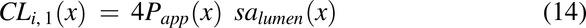
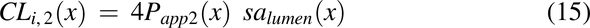

where CLi,2(x) is the diffusional clearance when radial diffusion is the rate-limiting step, and CLi,3(x) is the diffusional clearance for the intracellular lipid compartment by accounting for the difference in the surface area between the plasma membrane and intracellular lipids (1% plasma membrane). Papp2 is the modified apparent permeability when radial diffusion is the rate-limiting step and is modified by a radial diffusion function (eq. 18) to slow radial diffusion as the pulse approaches the end of the colon:
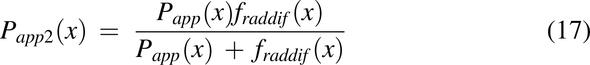
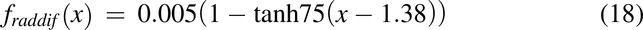
The diffusional clearance out of membranes, CLo(x), is dependent on membrane partitioning (Korzekwa et al., 2012). Therefore, radial diffusion out of the membranes (eq. 19) and membrane partitioning (eq. 20) can be explained by the following equations:


where fum is the fraction unbound in microsomes.
Transporter Expression for P-gp and Oatp2b1, P-gp(x) and Oatp(x)
To simulate the impact of transporters P-gp and Oatp2b1, reported transporter levels were used (MacLean et al., 2010; Mai et al., 2021). Transporter expression use and normalization was performed in the same manner as that described previously (Nagar et al., 2017). The P-gp and normalized Oatp2b1 expression functions are shown in Fig. 2, H and I, respectively. This led to the development of Michaelis-Menten saturation functions:
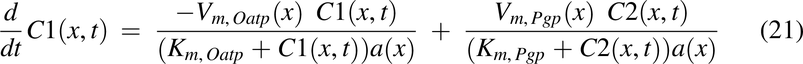

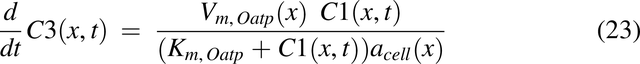
where
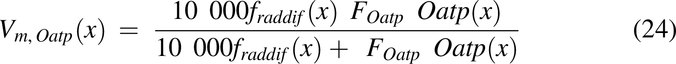

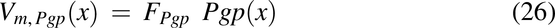

To make radial diffusion rate limiting for luminal uptake in the descending colon, the radial diffusion function, fraddif(x) was used. FOatp and FP-gp are the factors to convert transporter per mg mucosal tissue to mg drug transported per hour per unit volume of lumen for Oatp and apical membrane for P-gp, respectively.
DIG is known to be a P-gp substrate, whereas GLY relies on both Oatp and P-gp (El-Kattan and Varma, 2012; Estudante et al., 2013; Suzuki et al., 2014). Presence of food is reported to inhibit Oatp2b1, leading to PK differences between fasted and fed groups (Lee et al., 2020). The following empirical values, based upon preliminary optimization steps using the observed data, were used for transporter functions for DIG (P-gp) and GLY (P-gp and Oatp).
For DIG, Km,P-gp = 9000 µM, and FP-gp = 150 for all groups. For GLY, Km,P-gp = 50 µM, and FP-gp = 5000 for all groups. GLY fasted 2 hours FT and fasted 1 hour FT groups used a Km,Oatp = 5 µM, whereas the fed group used a Km,Oatp = 50 µM. Fasted 2 hours FT group used FOatp = 3.5, whereas the fasted 1 hour FT and fed group used a FOatp = 0.2. Thus, Oatp activity had to be reduced for GLY datasets when food was present.
Solution dosing input and disposition equations:
From in vivo data with different feeding times postdose, it is apparent that 1) some of the oral dose is immediately available for absorption, 2) feeding results in delayed release into the intestine, and 3) the longer the time before feeding, the less of the dose is retained. Therefore, drug input from the stomach was modeled by three unit pulse functions with a lag time (Fig. 3). The first pulse represents 10% of the dose that immediately enters the intestine, the second pulse represents the drug that is released into the intestine in the fasted state postdose, and the third pulse is the remaining dose released over a 20-hour period in the presence of food. The unit pulse functions for the three pulses are:

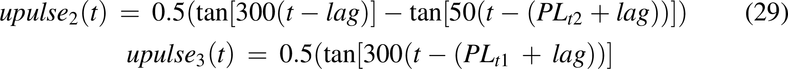

where lag = 0.1 hour, PLt1 = 0.1 hour, PLt2 = FT, and PLt3 = 20 hours; FT is the time food was reintroduced to animals after dosing drug. For fed animals, PLt2 = 0.001 hour was used.
Feeding times and input functions. (A) Experimental design for fasting and feeding schedule in rats. (B) Schematic for design of input functions. Of the total dose, 10% was input as an immediate pulse, and the remaining 90% was input as a fast + slow pulse: fast pulse under fasted conditions + slow pulse from addition of food for 22 hours. Green, fasted 0.5 hours FT with 18% fast + 72% slow pulse; brown, fasted 1 hour FT with 36% fast + 54% slow pulse; and red, fasted 2 hours FT with 72% fast + 18% slow pulse. (C) Input function used for the fasted 2 hours FT group is depicted as an example. Note the broken X- and Y-axes depicted as such for visual clarity.
The appropriate initial concentration and velocity in the duodenum was achieved by multiplying the upulse functions by the dosing concentration and a volume correction factor:
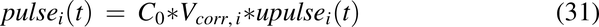
where C0 = dose/Vs,o mg/mL, and Vs,o is the volume of water introduced into the stomach with the drug (1 ml/kg). The Vcorr term is the volume correction factor for each pulse necessary to achieve the correct velocity entering the intestine:
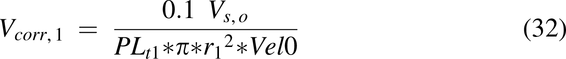

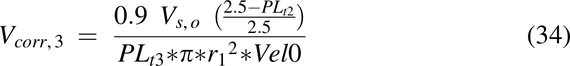
where Vel0 is the velocity at x = 0.
Drug solution disposition in the rat intestine was modeled for drug concentrations in the lumen, C1(x,t); apical membrane, C2(x,t); enterocyte cytosol, C3(x,t); and optional partitioning into intracellular lipids, C4(x,t), with the following PDEs:
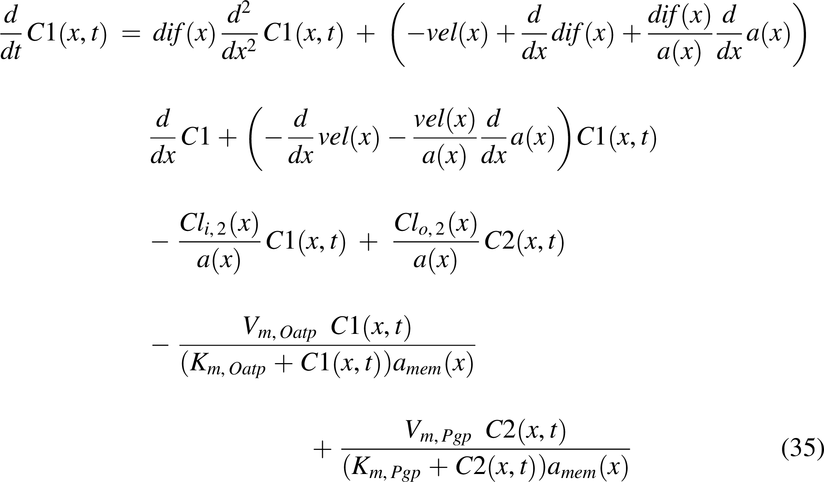
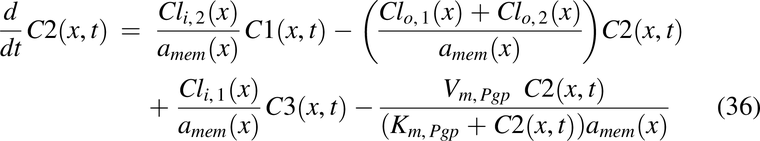

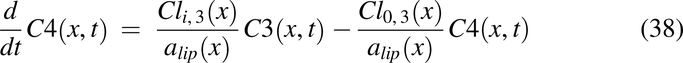
with initial conditions, C1(t, 0) = pulse1(t) + pulse2(t) + pulse3(t),
C1(0, x) = C1,0 (where C1,0 is defined as the concentration of pulse1(t) at t = 0),
C1(t, 1.45) = 0, C2(0, x) = 0, C2(t, 0) = 0, C2(t, 1.45) = 0, C3(0, x) = 0, C3(t, 0) = 0, C3(t, 1.45) = 0, C4(t, 0) = 0, C4(0, x) = 0, C4(t, 1.45) = 0.
Systemic PK and disposition functions:
The movement of drug from the enterocyte cytosol into the systemic PK model was modeled by the input function:
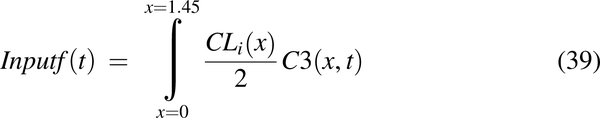
Experimentally collected intravenous data were modeled with two-compartmental PK models, and were used to generate systemic disposition functions. The systemic disposition functions were combined with the input function (eq. 32) to simulate oral PK profiles.
Methods for numerical solutions:
All models were developed using Mathematica 12.3.1. Intravenous data were fit using a NonLinearModelFit with a PrecisionGoal → Infinity and 1/Y weighting. ODEs and PDEs were simulated using the NDSolve function. PDEs were solved using the method of lines with default step sizes, SpatialDiscretization → TensorProductGrid, DifferenceOrder →2, and grid x-coordinates defined as follows:

Input and experimental data:
Permeability data from Caco-2 cells were obtained from the literature (Table 1). An exposure overlap coefficient (EOC) (Holt et al., 2019) was calculated to compare the simulated C-t profiles to the experimental oral PK profiles. An interpolation function was generated from the experimental oral C-t data (Interpolation function in Mathematica with Method → Spline and InterpolationOrder → 1). Since experimental clearances were used, the simulated C-t profile was normalized to have the same area under the curve (AUC) as the experimental profile. The overlap AUC was obtained by integrating the minimum of the two C-t functions. Lastly, the EOC was calculated as the overlap AUC/experimental AUC. The value of the EOC ranges between zero, no overlap, and one, complete overlap.
Physicochemical properties, microsomal physicochemical partitioning, and Caco-2 permeability data for drugs
Results
Rat Intestinal Measurements
Dimensions of the rat intestine were measured experimentally and used to develop the intestinal model (Fig. 1A). Fig. 2 shows the in-house generated velocity, cross-sectional surface area, fasted pH, and fed pH along the length of the rat intestine. In fed rats, the pH began at ∼6 in the duodenum and gradually increased to ∼7.5 in the ileum. The pH rapidly decreased to ∼5.5 in the cecum, where it remained until the distal colon (Fig. 2G). In fasted rats, the pH started higher at ∼6.5 in the duodenum and was maintained until the J4 segment. The pH in the ileum of fasted rats matched that of the fed group at ∼7.5 before decreasing back to ∼6.5 in the cecum and gradually declining along the colon (Fig. 2F). The fasted group had a significantly higher pH in the duodenum, J1, J2, cecum, and proximal colon segments (Supplemental Materials; Supplemental Table 1).
In both fed and fasted states, the velocity decreased as the charcoal plug moved along the intestine from the duodenum to the ileum (Supplemental Materials; Supplemental Tables 2 and 3). There was no statistically significant difference in the position versus time data between fasted and fed rats, so a single average velocity function was calculated and used to describe vel(x) (Fig. 2A).
Pharmacokinetics of AML, DIG, and GLY After Intravenous and Oral Administration
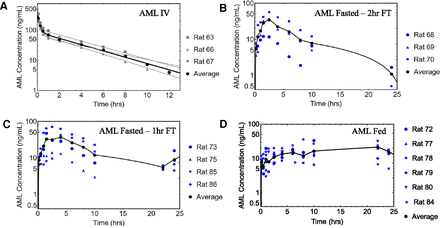
The individual and naïve-pooled average rat (n = 3) intravenous data for AML, DIG, and GLY were best described by a two-compartment model and are shown in Figs. 4A, 5A, and 6A, respectively. The parameter estimates and metrics for the naïve-pooled average datasets for all three drugs upon a single intravenous bolus dose are listed in Table 2.
Individual and naïve-pooled average profiles for AML. (A) Intravenous data (gray, individual; black, naïve-pooled average) and 2C-fitted lines. (B) PO data for fasted 2 hours FT, (C) PO data for fasted 1 hour FT, and (D) PO data for fed group. Data displayed in blue indicate individual rat profiles. The black dots and line indicate the naïve-pooled average of the individual rat datasets.
Macro- and microcompartmental PK parameter estimates and metrics of AML, DIG, and GLY calculated with a two-compartmental model for naïve-pooled average rat (n = 3) upon an intravenous bolus dose
The naïve-pool average estimates are listed as estimate ± standard error.
The individual and naïve-pooled average rat oral data for AML are shown in Fig. 4. The observed Cmax and time to achieve Cmax (tmax) values for the fasted 2 hours FT, fasted 1 hour FT, and fed groups are listed in Table 3. The tmax for the Fed group was 21.8 hours and was statistically different from the fasted groups (P = 0.02 with one-way ANOVA and posthoc Tukey’s honest significant difference test). The individual and naïve-pooled average rat oral data for DIG are shown in Fig. 5, and the observed Cmax and tmax values for the fasted 1 hour FT, fasted 0.5 hours FT, and fed group are listed in Table 3. The individual and naïve-pooled average rat oral data for GLY are shown in Fig. 6, and the observed Cmax and tmax values for the fasted 2 hours FT, fasted 1 hour FT, and fed group are in Table 3. There was no significant difference in Cmax and tmax values among the DIG and GLY groups. The interanimal variability for all DIG and GLY PO groups was large and may have contributed to poor prediction with the mean datasets (Fig. 7).
Individual and naïve-pooled average profiles for DIG. (A) Intravenous data (gray, individual; black, naïve-pooled average) and 2C-fitted lines. (B) PO data for fasted 1 hour FT, (C) PO data for fasted 0.5 hours FT, and (D) PO data for fed group. Data displayed in blue indicate individual rat profiles. The black dots and line indicate the naïve-pooled average of the individual rat datasets.
Individual and naïve-pooled average profiles for GLY. (A) Intravenous data (gray, individual; black, naïve-pooled average) and 2C-fitted lines. (B) PO data for fasted 2 hours FT, (C) PO data for fasted 1 hour FT, and (D) PO data for fed group. Data displayed in blue indicate individual rat profiles. The black dots and line indicate the naïve-pooled average of the individual rat datasets.
Predicted C-t profiles with oral solution dose under different feeding conditions. Observed naïve-pooled average (blue points and line) and model-predicted (red) C-t profiles are overlaid upon normalization of AUC as described in Materials and Methods and Results. The green-shaded region represents the overlapping area from time zero to last observed data collection time. Results are shown for (A) AML fasted 2 hours FT, (B) AML fasted 1 hour FT, (C) AML fed, (D) DIG fasted 1 hour FT, (E) DIG fasted 0.5 hours FT, (F) DIG fed, (G) GLY fasted 2 hours FT, (H) GLY fasted 1 hour FT, and (I) GLY fed.
Observed and predicted Cmax, tmax, and EOC for AML, DIG, and GLY. Observed metrics are listed based on the naïve-pooled datasets.
Prediction of Absorption with the Continuous Absorption Model
Fig. 7 shows observed and predicted C-t profiles for three drugs dosed in solution under different feeding conditions. The predicted curves were normalized to the observed AUC by optimizing the first-pass metabolism (FgFh or the product of fractions escaping gut wall metabolism and hepatic metabolism) value to obtain the experimental AUC. Therefore, only the rate of absorption and shape of the C-t profiles were predicted (see Table 3 for predicted Cmax and tmax). The areas in green represent the overlap between the observed and predicted C-t profiles. The numerical values of the EOCs along with experimental and predicted Cmax and tmax are listed in Table 3. The AML Cmax and tmax predictions across the groups were in good agreement with the observed data. For DIG and GLY, the predicted tmax values were longer than mean observed values for all groups (Fig. 7; Table 3). Overall, the shape of the C-t profiles for all three drugs was generally well predicted under all three feeding conditions, with EOC values ranging from 0.80 to 0.97.
Discussion
The goals of this work were to 1) develop a continuous rat intestinal absorption model and 2) develop a modeling framework for prediction of food effects in oral drug absorption. We specifically aimed to study the impact of feeding time on oral drug absorption for three model drugs in a rat model. Utilizing the previously published human continuous intestinal absorption model, a rodent model was developed using species-specific physiologic parameters as a function of length ×. The inclusion of an explicit membrane compartment allowed for accurate modeling of the efflux transporter P-gp and membrane partitioning, whereas the inclusion of an intracellular lipid compartment allowed for modeling of lipid partitioning. The rat intestinal model was built based on in-house experimental measurements of intestinal dimensions, velocity, and pH. Novel aspects of the work include the following characteristics in a continuous intestinal model: 1) inclusion of experimentally measured fasted and fed intestinal pH profiles, 2) inclusion of an experimentally measured velocity function, 3) inclusion of efflux and uptake transporter expression data, and 4) development of input functions based on experimental fasting and feeding times to recapitulate differences in stomach emptying in the presence of food.
Although rodent models are useful for proof-of-concept exploration, they may not be useful to scale up complex oral absorption processes to man. The most notable species differences are the structure of the stomach and the composition of the intestine. The human stomach is a single gastric compartment, whereas the rodent stomach is both glandular, which contains glands that secrete gastric acid, and nonglandular. A limiting ridge, a thickened portion of lamina propria, separates these portions (Kararli, 1995; DeSesso and Jacobson, 2001). This limiting ridge and dual-portioned stomach may account for why food is present in the rat stomach after a 12-hour fast, whereas the human stomach is over 90% empty after only 4 hours of fasting (Read et al., 1986; Jeffrey et al., 1987). Also, the duodenum, jejunum, and ileum make up 4%, 38%, and 58% of the small intestine, respectively, in humans and 8%, 90%, and 2% of the small intestine in rats. Additionally, the cecum is 26% of the length of the large intestine in rats but is only 5% in humans (Kararli, 1995; Vdoviakova et al., 2016). Humans have three enlargement factors that contribute to the increased absorptive surface area: Kerckring’s folds, villi, and microvilli, whereas rats lack Kerckring’s folds. Although humans and rats have a similar pH range (∼6–8) and trend along the intestine, humans have a gastric pH around 1–2.5, whereas rats have a more alkaline gastric pH around 3 to 4 (Ward and Coates, 1987; Evans et al., 1988). Humans have two primary intestinal uptake transporters, OATP1A2 and OATP2B1, whereas rats have several (Suzuki et al., 2012; Takeda et al., 2021). Rats have two mdr1 genes, mdr1a and mdr1b, whereas humans only have one MDR1 gene. For both species, the protein expression of P-gp increases from the proximal to distal regions (Brady et al., 2002). Lastly, rats do not possess a gallbladder, which stores and releases concentrated bile in humans when food is present. Bile salts can increase the dissolution rate and solubility of lipophilic compounds, aiding in their intestinal absorption (Kararli, 1995).
The factors stated above can additionally contribute to vast interanimal variability in rat oral absorption profiles. It has been documented that rats with the same dosing conditions (same compound, dose, route of administration, formulation, dosing regimen, and feeding) exhibit AUC ratios of greater than 2 (Daublain et al., 2017). Along with distinctive physiologic factors, feeding regimens, including volume and frequency of food consumption, could introduce variability. Animals given food ad libitum will have variable self-imposed feeding regimens. Even when food is removed from the cages of rats in fasted groups, rats are known to eat anything available to them, including their bedding and engaging in coprophagy. The present studies were not conducted using metabolic cages, and these factors may have contributed to lack of differences in transit times between fasted and fed groups in gastrointestinal motility studies (Supplemental Materials; Supplemental Tables 2 and 3).
Incorporating the ability to model various aspects of food effects to predict PK of oral drugs is important (Lin and Wong, 2017). The Advanced Compartmental Absorption and Transit model allows for the modeling of food effects by varying physiologic parameters that influence drug absorption, such as gastric pH and emptying time along with bile salt concentrations (Cheng and Wong, 2020). PBPK software built with compartmental absorption models have the capability to evaluate various food effects. PBPK modeling was used to discern that oral absorption of delayed-release zolpidem depended on the formulation in the fasted state but depended on gastric emptying in the fed state (Andreas et al., 2017). The impact of food on drug solubility and resulting oral absorption was evaluated with a PBPK modeling software in another study (Zhang et al., 2014). The present work focused on evaluating the impact of feeding time on oral absorption. Although human studies usually detail fasting and postdosing feeding times, these details are not provided in preclinical oral dosing studies. This work illustrates the critical need to document and model appropriately the absence and presence of food, including feeding time, in oral dosing studies. The rat continuous intestinal absorption model developed here included separate intestinal pH functions for fasted and fed conditions (Fig. 2). In addition, we developed a drug input function that accounted for the introduction of food postdosing (Fig. 3). The drug input function was based on experimental design (Fig. 3A), as well as the observed slower slope of the terminal C-t profiles upon oral dosing when compared with the intravenous C-t profiles (Figs. 4–6), indicating that absorption was occurring even at later timepoints. Delayed absorption in the presence of standard or high-fat food has been reported for several BCS class 1–4 drugs in humans (Deng et al., 2017). With the input functions incorporating impact of feeding time, the continuous absorption model predicted with marked accuracy the observed mean C-t profiles for all groups for the three drugs tested (Fig. 7). These results indicate the utility of the modeling framework to evaluate the impact of feeding time on oral absorption.
As with the compartmental PBPK software, active transport is easily incorporated into the continuous absorption model. DIG is a well-known substrate of P-gp, and inhibition of this transporter has been shown to increase the AUC of DIG in rats (Suzuki et al., 2014). Predictions of DIG using only a passive permeability model overpredicted the Cmax in both fasted groups (data not shown). The addition of P-gp improved the accuracy of C-t predictions for DIG. For GLY, a known transporter substrate for both P-gp and Oatp (El-Kattan and Varma, 2012; Estudante et al., 2013), improved predictions were obtained when transporters were added. It was interesting that reduced Oatp activity had to be used for groups in the presence of food, which aligns with the observed Oatp inhibition in the presence of food (Lee et al., 2020).
The present work includes studies with three drugs as proof of concept. The continuous absorption model is not a validated model, and its use for predicting oral absorption of a variety of small molecules will be necessary for validation in the future. Refinements to the model and to the input function will likely be necessary to include complexities such as type of food, formulation-food interactions, and acute drug-food interactions. The rat model is not intended for eventual scaling to humans but instead to provide a species-specific framework to evaluate complexities including a wide variety of food effects on oral absorption. Work is currently underway to use this rat model to evaluate the impact of formulation design on oral absorption. Additionally, we are incorporating gut metabolism into the model. A similar model for the mouse is currently under development in our laboratory and is expected to provide additional insights into oral absorption in the presence and absence of drug metabolizing enzymes and transporters, and with a variety of formulations. Together, this work will advance refinement of the original human continuous absorption model in a species-specific manner and will broadly provide mathematical tools to evaluate various types of food and formulation effects on oral drug absorption across species. It is hoped that the code provided for this model will encourage others to refine, incorporate additional intestinal/drug features, and validate this framework.
Authorship Contributions
Participated in research design: Radice, Korzekwa, Nagar.
Conducted experiments: Radice.
Performed data analysis: Radice, Korzekwa, Nagar.
Wrote or contributed to the writing of the manuscript: Radice, Korzekwa, Nagar.
Footnotes
- Received January 14, 2022.
- Accepted March 17, 2022.
This work was supported by National Institutes of Health National Institute of General Medical Sciences [Grant 2R01-GM104178] and [Grant 2R01-GM114369] (to S.N. and K.K.).
The authors have no financial disclosures and no conflicts of interest to report.
↵
 This article has supplemental material available at dmd.aspetjournals.org.
This article has supplemental material available at dmd.aspetjournals.org.
ABBREVIATIONS
- A
- aqueous phase
- ACN
- acetonitrile
- AML
- amlodipine
- AUC
- area under the curve
- BCS
- biopharmaceutics classification system
- C1
- lumen
- C2
- apical membrane
- C3
- enterocyte cytosol
- C4
- intracellular lipid
- C5
- portal blood
- CE
- collision energy
- C-t
- concentration-time
- CXP
- collision cell exit potential
- DIG
- digoxin
- DP
- declustering potential
- EOC
- exposure overlap coefficient
- FA
- formic acid
- FT
- feeding time
- GLY
- glyburide
- J
- jejunum
- LC-MS/MS
- liquid chromatography and tandem mass spectrometry
- NMP
- 1-Methyl-2-pyrrolidinone
- Oatp
- organic anion transporter protein
- PBPK
- physiologically based pharmacokinetic model
- PDE
- partial differential equation
- PEG-400
- polyethylene glycol 400
- P-gp
- P-glycoprotein
- PK
- pharmacokinetic
- PO
- peroral
- t
- time
- tmax
- time at which maximum concentration Cmax is achieved
- x
- distance
- Copyright © 2022 by The American Society for Pharmacology and Experimental Therapeutics