Advertisement
Research ArticleSpecial Section on Prediction of Human Pharmacokinetic Parameters from In Vitro Systems

Utility of In Vitro Systems and Preclinical Data for the Prediction of Human Intestinal First-Pass Metabolism during Drug Discovery and Preclinical Development

Fredrik H. Karlsson, Salim Bouchene, Constanze Hilgendorf, Hugues Dolgos and Sheila Annie Peters
Drug Metabolism and Disposition December 2013, 41 (12) 2033-2046; DOI: https://doi.org/10.1124/dmd.113.051664

Abstract

A growing awareness of the risks associated with extensive intestinal metabolism has triggered an interest in developing robust methods for its quantitative assessment. This study explored the utility of intestinal S9 fractions, human liver microsomes, and recombinant cytochromes P450 to quantify CYP3A-mediated intestinal extraction in humans for a selection of marketed drugs that are predominantly metabolized by CYP3A4. A simple competing rates model is used to estimate the fraction of drug escaping gut wall metabolism (fg) from in vitro intrinsic clearance in humans. The fg values extrapolated from the three in vitro systems used in this study, together with literature-derived fg from human intestinal microsomes, were validated against fg extracted from human in vivo pharmacokinetic (PK) profiles using a generic whole-body physiologically-based pharmacokinetic (PBPK) model. The utility of the rat as a model for human CYP3A-mediated intestinal metabolism was also evaluated. Human fg from PBPK compares well with that from the grapefruit juice method, justifying its use for the evaluation of human in vitro systems. Predictive performance of all human in vitro systems was comparable [root mean square error (RMSE) = 0.22–0.27; n = 10]. Rat fg derived from in vivo PK profiles using PBPK has the lowest RMSE (0.19; n = 11) for the prediction of human fg for the selected compounds, most of which have a fraction absorbed close to 1. On the basis of these evaluations, the combined use of fg from human in vitro systems and rats is recommended for the estimation of CYP3A4-mediated intestinal metabolism in lead optimization and preclinical development phases.

Introduction

To minimize the risk for low oral drug bioavailability, compounds are routinely optimized for solubility, permeability, and hepatic metabolism during lead optimization. However, there are no effective screens to minimize intestinal metabolism. Human enterocytes express a variety of drug metabolizing enzymes (Kaminsky and Zhang, 2003), with the most important of these being cytochrome P450 (P450) and uridine 5′-diphospho-glucuronosyltransferases (UGTs). Among UGT isoforms, UGT1A8 and UGT1A10 show gut-specific expression patterns, whereas the highly expressed intestinal isoforms UGT1A1 and UGT2B7 are also found in other organs (Kaminsky and Zhang, 2003; Court et al., 2012). The gut wall UGT expression levels can exceed those in the liver (Ohno and Nakajin, 2009; Court et al., 2012). Intestinal metabolism can occur in the gut lumen, via esterases (Taketani et al., 2007) and microflora-mediated reduction and hydrolysis (Goldin, 1990). With its broad specificity and high abundance in the intestine (Paine et al., 2006; Thelen and Dressman, 2009), CYP3A is frequently implicated in gut metabolism. Compared with the liver, CYP3A expression and cofactor levels in the small intestine are lower overall (Paine et al., 1997). In addition, functionally mature enterocytes reside only in villous tips. However, whereas hepatic metabolism is limited by plasma protein binding and blood perfusion rates, CYP3A-mediated intestinal metabolism is limited only by drug permeability. Furthermore, long intestinal transit times provide increased opportunity for substrate presentation to enzymes, especially with the synergistic interplay of CYP3A and P-glycoprotein (P-gp) on dual substrates (Benet et al., 2004; Siissalo and Heikkinen, 2013). Extensive intestinal metabolism is often associated with low oral bioavailability and high interindividual variability (Hellriegel et al., 1996). The heterogeneous distribution of enzymes along the gut results in a regional variation in gut extraction. In addition, extensive gut metabolism also increases the risk for drug–drug interactions, the magnitude of which depends on the fraction escaping gut metabolism (fg) of both the substrate and the inhibitor (Peters et al., 2012). The risks associated with intestinal metabolism highlight the need for robust, quantitative models for the prediction of human fg.

To facilitate the prediction of fg, human in vitro systems such as intestinal tissue in Ussing chambers (van de Kerkhof et al., 2006; Sjöberg et al., 2013) and human intestinal/jejunal microsomes (Gertz et al., 2010, 2011; Kadono et al., 2010) have been evaluated. However, their quantitative utility is limited by a lack of consensus on the appropriate scaling factors and a low availability of high-quality tissue. The first objective of this work is to compare the performance of three commonly available in vitro systems—human liver microsomes (HLMs), human intestinal S9 fractions, and recombinant P450s—for predicting intestinal extraction. In vitro intrinsic clearance was determined in intestinal S9 fractions, HLMs, and recombinant P450s for 16, 12, and 11 compounds, respectively. Along with these, human intestinal microsomal data from the literature (Gertz et al., 2010) were evaluated for a common subset of 10 compounds. A simplified model was utilized to convert in vitro intrinsic clearances to fg. The resulting fg has been validated against fg derived from human pharmacokinetic (PK) data using a generic whole-body physiologically-based pharmacokinetic (PBPK) model. The traditional indirect method of determining gut extraction from in vivo pharmacokinetic data provides intestinal availability (Fg), the product of the fraction absorbed (fa) and fg, where fa must be accurately estimated or assumed to equal 1.

The rat does not predict human intestinal loss (Bueters et al., 2013), in line with known species differences in intestinal enzymes and their expression levels (Cao et al., 2006; Mitschke et al., 2008). In contrast, the rat is a good model for human intestinal absorption (Cao et al., 2006). For a high-permeability drug, intestinal extraction becomes dependent on permeability rather than intrinsic clearance of the drug. The greater the permeability, the greater is the ability to escape interaction with enzymes. Hence, differences in enzyme activity will have little impact on intestinal extraction. Therefore, the rat should be a good model for human fg, at least for high-permeability compounds. In addition, Bueters et al. (2013) studied compounds that were metabolized by both P450 and UGT enzymes. It is of interest to compare the results from Bueters et al. (2013) with an investigation focused on CYP3A substrates. The second objective is therefore to explore the possibility of using the rat as a model of human CYP3A-mediated intestinal metabolism. The 16 compounds selected for this study are predominantly metabolized by CYP3A and are known to be extracted in the human gut. Complete datasets with intravenous and oral PK profiles were available for 13 compounds in humans and 11 in rats.

Materials and Methods

Chemicals and Reagents

All 16 marketed drugs selected for this study were provided by AstraZeneca R&D Compound Management (Mölndal, Sweden). EDTA, sucrose, glucose, bovine serum albumin, NADPH, UDP-glucuronic acid, and SDS were purchased from Sigma-Aldrich (Malmö, Sweden). Carbogen was obtained from AGA Gas AB (Sundbyberg, Sweden), Pefabloc SC (protease inhibitor) was from Boehringer Mannheim (Mannheim, Germany), and NaOH was from AkzoNobel (Skoghall, Sweden). Potassium dihydrogen phosphate, dipotassium hydrogen phosphate trihydrate, K-Na-tartrate, formic acid, and Folin–Ciocalteu reagent were purchased from Merck KGaA (Darmstadt, Germany), high-performance liquid chromatography–grade acetonitrile was from Rathburn (Walkerburn, UK), and 5,5-diethyl-1,3-diphenyl-2-iminobarbituric acid was from Sigma-Aldrich (St. Louis, MO). All other chemicals and solvents were at least of analytical grade and were obtained from commercial sources.

In Vitro Systems

Human Intestinal S9 Fractions.

Human intestinal S9 fractions were prepared in-house from fresh, viable tissue obtained from surgical resections at Sahlgrenska University Hospital (Gothenburg, Sweden). The jejunum specimens were resected during gastric bypass surgery upon receiving informed written consent and ethical approval from the regional ethical committee in Gothenburg, Sweden. Intestinal segments from two female and two male donors (aged 47–63 years) were used in this study. Directly after surgical removal, the tissues were stored in ice-cold constantly carbogenated (95% O2, 5% CO2) Krebs-Ringer buffer (pH 7.4), with 5 mM glucose, and transported to the laboratory within 30 minutes.

Rat Intestinal S9 Fractions.

Rat intestinal S9 fractions were both prepared in-house and purchased from tebu-bio (Roskilde, Denmark). All procedures involving animals were reviewed and approved by the Committee on Animal Experimentation (Gothenburg, Sweden). The animals had free access to water and food (R3; Lactaim AB, Vadstena, Sweden) and were housed at the AstraZeneca R&D Department of Laboratory Animal Resources. Intestinal tissues were extracted from six female and two male Sprague-Dawley rats (Harlan Laboratories, Horst, The Netherlands) that weighed approximately 250 g and were aged 11–13 weeks. To maintain systemic circulation during the excision of the intestine, the rats were anesthetized with isoflurane. The duodenum (10 cm) and the jejunum (following 25 cm) were carefully rinsed with cold sucrose-EDTA buffer (1 mM EDTA, 10 mM KPO4, 250 mM sucrose, pH 7.4), and submerged in ice-cold carbogenated (95% O2, 5% CO2) buffer (1 mM EDTA, 10 mM KPO4, 250 mM sucrose, pH 7.4) during transport to the isolation laboratory.

Preparation of Intestinal S9 Fractions.

Rat intestinal mucosa came from at least two animals and was pooled, whereas the human sample was always from one donor. All procedures were carried out within 30–45 minutes from resection; during this time, the tissue was kept in ice-cold buffer under continuous carbogen bubbling to maintain viability. The muscular layer from human jejunum was removed and the mucosa and submucosa were flattened out with mucosa facing upward on a filter paper placed on a cold-block. The rat duodenum and jejunum were cut open into 5-cm pieces and straightened out on cold filter paper with the mucosa facing upward. From here, rat and human tissue were treated in the same way using prechilled equipment in all steps of the procedure. All steps were carried out on ice. The intestinal mucosa was quickly scraped off with a cold microscope glass slide, immediately transferred into a glass homogenizer, and submerged in ice-cold homogenization buffer containing protease inhibitors (1 mM EDTA, 10 mM KPO4, 250 mM sucrose, pH 7.4, 0.4 M Pefabloc SC), with approximately 4 ml buffer/g mucosa. Immediately after collection of the mucosa, the tissue was homogenized in a glass-Teflon homogenizer. The homogenization procedure was carried out on ice, alternating five strokes with 10 seconds of cooling. The resulting homogenate was diluted with homogenization buffer solution, yielding a final tissue to buffer ratio of 1:5 (1 mg to approximately 1 µl). The homogenate was further processed by centrifugation for 20 minutes (9000g, 4°C) in a Beckman Ultracentrifuge (Beckman Coulter, Brea, California). The supernatant (S9 fraction), containing plasma membranes, endoplasmic reticulum, and cytosol, was then collected and dripped frozen in liquid nitrogen and stored at −80°C.

Protein Determination of S9 Fractions.

The protein determination was carried out according to the process by Markwell et al., (1978) using Folin–Ciocalteu reagent. The S9 fractions were diluted 50× and 100× in homogenization buffer (1 mM EDTA, 10 mM KPO4, 250 mM sucrose, 0.4 M Pefabloc SC, pH 7.4). The absorbance was then measured at 660 nm with a Spectramax190 spectrophotometer (Molecular Devices, Sunnyvale, CA) and the protein concentration was calculated with SoftMax Pro 4.8 software (Molecular Devices) against a standard curve of 10–200 μg/ml bovine serum albumin in homogenization buffer.

HLMs and Recombinant P450.

HLMs were purchased from BD Biosciences (Erembodegem, Belgium) and constituted a pool of samples from more than 30 individuals. Recombinant P450s (rCYPs) were obtained from Cypex Limited (Dundee, UK).

Incubation with Intestinal S9 Fractions

For human intestinal S9, all reactions were carried out in 96-well plates at a total protein concentration of 6 mg/ml in 0.1 M phosphate buffer (pH 7.4), in the presence of 1 mM NADPH and 1 μM substrate in an incubation volume of 100 μl. For the rat intestinal S9, incubation conditions were varied with respect to protein concentrations (0.4, 1, and 3 mg/ml) and test compound concentrations (1 and 20 µM). Incubations were performed in duplicate with three negative controls (without enzyme, without NADPH, and without compound). All reactions were carried out under continuous shaking in a THERMOstar incubator (Lab Vision, Thermo Fisher Scientific Inc., Kalamazoo, MI) set to 37°C and 660 rpm. At time points of 1, 5 10, 20, 40, and 60 minutes, a sample of 10 μl incubate was removed from the reaction plate and quenched in 50 μl ice-cold stop solution (50% acetonitrile (ACN) with 0.2 µM analytical volume marker 5,5-diethyl-1,3-diphenyl-2-iminobarbituric acid). Stop plates were centrifuged for 20 minutes (4000g, 4°C; Eppendorf International, Hamburg, Germany). A volume of 30 µl supernatant solution was transferred to new plates and diluted with 30 μl purified water with a Sciclone ALH3000 automated pipetting machine (Caliper Life Sciences, Hopkinton, MA). Nonspecific binding to intestinal S9 was not measured.

Incubation with Recombinant P450s

The enzymes studied were human recombinant CYP1A2, CYP2C8, CYP2C9, CYP2C19, CYP2D6, and CYP3A4. The incubations were performed in duplicate in 96-well plates with 200 μl 0.1 M phosphate buffer (pH 7.4), 1 mM NADPH, and 1 μM test compound at 37°C under continuous agitation at 300 rpm in a shaking incubator (THERMOstar). The concentration of recombinant P450 enzymes was 0.05 pmol/μl. At time points of 0, 7, 15, and 30 minutes, 30 μl incubation solution was transferred into a plate with 90 μl ice-cold stop solution (50% ACN with 0.2 µM analytical volume marker 5,5-diethyl-1,3-diphenyl-2-iminobarbituric acid). The stop plate was centrifuged for 20 minutes (4000g, 4°C), and a volume of 60 μl supernatant was transferred to a new plate and diluted with 60 μl purified water using a Sciclone ALH3000 automated pipetting machine.

Incubation with HLMs

Incubations with HLMs were carried out in replicate plates with 200 μl 0.1 M phosphate buffer (pH 7.4), 1 mM NADPH, and 1 μM test compound at 37°C under continuous agitation at 300 rpm in a shaking incubator (THERMOstar). Microsomal concentration was 0.5 mg/ml. At time points of 0, 7, 15, and 30 minutes, 30 μl incubation solution was transferred to a plate filled with 90 μl ice-cold stop solution (50% ACN and internal standard 5,5-diethyl-1,3-diphenyl-2-iminobarbituric acid). The stop plate was centrifuged for 20 minutes (4000g, 4°C), and 60 μl supernatant was transferred to a new plate and then diluted with 60 μl purified water using an automated pipetting machine Sciclone ALH3000. Nonspecific binding to HLM was not measured.

Analysis

The concentration of the test compounds in all incubated samples was analyzed by high-performance liquid chromatography connected to a triple quadrupole–tandem mass spectrometer utilizing electrospray ionization and multiple reaction monitoring. The liquid chromatography–mass spectrometry system consisted of a quaternary Agilent 1100 series pump (Agilent Technologies, Waldbronn, Germany), a CTC HTS Pal autosampler (CTC Analytics, Zwingen, Switzerland) equipped with a 20 µl loop, a 25 µl syringe (Hamilton Bonaduz AG, Bonaduz, Switzerland), a 6-port 2-position switching valve for automated column selection (Cheminert, C2V-2005D-CTC, 07K-0800C; VICI AG, Schenkon, Switzerland), a 6-port 2-position switching valve to enable diversion of the chromatographic front to waste (Cheminert, C2-10060, 00K-0712C; VICI AG), a column oven (model 7990R-1, Grace; Alltech Associates Inc., Lokeren, Belgium), and a Quattro Ultima triple-quadrupole mass spectrometer (Waters Corp., Milford, MA). Instrument control and data processing were done with Waters MassLynx 4.1 software including QuanOptimize and QuanLynx (Waters Corp.). Samples were kept at 11°C. Chromatography was performed on a Waters XBridge C18 (2.5 μm, 2.1 × 20 mm) with gradient elution, over 1.65 minutes at a flow rate of 0.7 ml/min. The binary solvent system was composed of water with 2% (v/v) ACN and 0.2% (v/v) formic acid (A) and 100% (v/v) ACN with 0.2% (v/v) formic acid (B). The compound specific conditions of mass spectrometry and chromatography are summarized in Table 1.

View this table:
TABLE 1

Mass spectrometric conditions and the chromatographic retention time for each compound

Positive ionization mode was used as standard.

Modification of the Analytical Protocol.

A higher final dilution of 1/10 was also tested to improve the sensitivity for the analysis of samples incubated with rat intestinal S9. To check the enzymatic activity of rat intestinal S9 fraction batches, metabolite formations of two well-established CYP3A substrates were followed: 1-hydroxymidazolam, metabolite of midazolam and fexofenadine, and metabolite of terfenadine.

CLint,g Calculation

Parent compound concentrations were plotted versus time in a semilogarithmic scale to linearize the exponential depletion describing approximately a first-order process. The enzymes are assumed to work at concentrations well below Km and to have a constant activity during the experiment. An exponential disappearance of the compounds validates the assumption that the concentrations are indeed well below Km.

The first-order rate constant was divided by the enzyme or protein concentration to obtain the intrinsic clearance (CLint) in the incubation.

Data from HLM incubations are transformed into intestinal intrinsic clearances (CLint,g) using two scalars, assuming that the substrates are mainly metabolized by CYP3A. An average CYP3A hepatic abundance of 155 pmol/mg protein and a combined intestinal CYP3A abundance of 70.5 nmol/mg protein (Yang et al., 2007) were used to convert hepatic intrinsic clearance to CLint,g. For the recombinant enzymes, CLint,g was calculated according to Eq. 1, using the published abundances of different P450 isoforms (P450i) (Paine et al., 2006) and measured intrinsic clearances (CLint,i) in the various sections of the small intestine: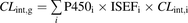Embedded Image(1)ISEFi is the intersystem extrapolation factor for the ith P450 isoform. For CYP1A2, CYP2C8, CYP2C9, CYP2C19, CYP2D6, and CYP3A4, the ISEF values for the recombinant system used (Cypex HR; Cypex, Dundee, Scotland, UK) were 0.16, 0.16, 0.09, 0.2, 0.15, and 0.25, respectively (Simcyp version 9.2; Simcyp Limited, Sheffield, UK).

For the intestinal S9 incubations, measured in vitro intrinsic clearances were scaled to the intestine, by using an empirical scaling factor of 0.167 × 105 mg protein, which was obtained by minimizing the overall error of the predicted fg with respect to fg derived from observed in vivo profiles using PBPK simulations. Thus, measured CLint values in microliters per minute per milligram of protein were multiplied by 1 (10−6 × 60 × 0.167 × 105 mg protein) to convert them to CLint,g in liters per hour.

Models for the Estimation of fg Using In Vitro CLint,g

Several models have been proposed for the determination of fg from CLint,g (Benet et al., 1999; Yang et al., 2007; Kadono et al., 2010). The most notable among these is the Qgut model (Yang et al., 2007), which resembles the well stirred liver model (Rowland et al., 1973) and is given by Eq. 2: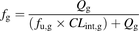Embedded Image(2)fu,g is the fraction of unbound drug in the enterocytes and CLint,g is the intrinsic metabolic clearance in the gut. Qg is given by Eq. 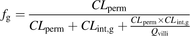3:Embedded Image(3)Qvilli is the human blood flow in the villi with a value of 18 l/h (Yang et al., 2007). CLperm is the permeability through the enterocytes and may be evaluated using the measured Caco-2 permeability (PCaco-2,pH7.4, expressed in 10−6 cm/s) and an estimate of the human small intestinal surface area, A, of 0.66 m2 (Yang et al., 2007) (Eq. 4):Embedded Image(4)Substituting for Qg from Eq. 3 in Eq. 2:Embedded Image(5)The predictive performance of the Qgut model has been shown to be best for fu,g = 1 (Yang et al., 2007). If fu,g is assumed to be 1, Eq. 5 can be rearranged to Eq. 6 on multiplying both the numerator and denominator with CLperm/Qvilli:Embedded Image(6)The Qgut model reduces to the simpler model of competing rates (Eq. 7) (Benet et al., 1999) if the product of CLint,g × CLperm is small compared with Qvilli:

Embedded Image(7)

Because drug delivery to the enzyme in the enterocytes is by drug permeability rather than by blood flow to the gut, gut metabolism is not expected to be limited by Qvilli. Thus Eq. 7 is a better physiologic representation of the system compared with the Qgut model. Equation 7 suggests that the fraction escaping gut metabolism is simply a ratio of the permeability to the competing rates of permeability and gut metabolism.

Estimation of First-Pass Intestinal Metabolism from In Vivo Pharmacokinetic Profiles Using PBPK Models

PBPK models describe the absorption, distribution, metabolism, and elimination of a drug in an organism, by mass balance equations in a closed circulatory system with organs represented as compartments. A generic previously described PBPK model (Peters, 2008a,b) built in-house using MatLab software (MathWorks Inc., Natick, MA) has been used in simulating the pharmacokinetic profiles. This model has 14 organs (adipose tissue, heart, lung, brain, muscle, bone, skin, stomach, spleen, pancreas, gut, liver, kidney, and thymus) represented as compartments and linked together by the arterial and venous blood compartments. Mass transfer between compartments is assumed to be perfusion limited and compartments are assumed to have a uniform drug distribution (well-stirred). There is an associated blood flow, tissue partition coefficient, and volume for each compartment. The tissue distribution model incorporated within the PBPK model estimates tissue/plasma partition coefficients (Kp) for the organs using compound characteristics such as lipophilicity (log P) and pKa, and the fraction of free drug in plasma, as well as composition of water, fat, and proteins in each of the tissues making up the compartments (Rodgers et al., 2005; Rodgers and Rowland, 2006). The somatic model is linked through the liver compartment to an absorption model with stomach, seven small intestinal compartments, and a colonic compartment. In each of the nine gastrointestinal compartments, intestinal scaling factors (ISFs) are used as multiplicative factors to permeability. ISFs have default values of 1 in the small intestinal compartments and 0.1 in the colon. A first-order rate constant, krenal, is calculated based on the glomerular filtration rate and fraction unbound in plasma. ka represents the rate of absorption for the different gastrointestinal compartments. A first-order biliary rate constant kbil accounts for the parent compound or its metabolite into bile. The enterohepatic recirculation (EHR) constant switches between 1 and zero to include or exclude emptying of the parent compound into the duodenal compartment. A nonzero value for CP is used to consider metabolite reconversion to the parent compound in the colon. Thus, the model provides for drug elimination through the intestine, kidney, and liver. The model does not incorporate differential enzyme expression levels in the gut compartments and therefore cannot be used to predict intestinal metabolism. However, it can be used to extract intestinal fg values from in vivo PK profiles by modulating ISFs to account for regional variation of intestinal availability.

Physicochemical Properties of the Tested Drugs Used as Input for the Model.

Table 2 shows the physicochemical properties of the compounds in this study.

View this table:
TABLE 2

Physicochemical properties of selected compounds

In vitro solubility data from in-house assays or literature were used as model input; pKa values were obtained using ACD 2011 software (ACD/Labs, Toronto, ON, Canada). Effective permeability (Peff) values were calculated from in vitro Caco-2 permeability, PCaco-2,pH6.5 in Eq. 8:Embedded Image(8)

In the absence of measured Caco-2 data, Peff was calculated using Eq. 9 (Winiwarter et al., 1998):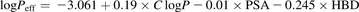Embedded Image(9)where C log P is the calculated octanol-water partitioning coefficient, PSA is the polar surface area, and HBD is the number of hydrogen bond donors, calculated using in-house routines.

Pharmacokinetic Data.

Pharmacokinetic data after i.v. and oral administration of a single dose of drug in healthy subjects and in rats (Table 3) were obtained for the selected compounds from the literature (Supplemental Table 1) or from AstraZeneca in-house databases. For every compound, the i.v. and oral data are from the same literature source.

PBPK Simulations to Extract fg from In Vivo PK Profiles.

The estimation of fg of a compound from its in vivo i.v. and oral concentration-time profiles using PBPK simulations was described by Peters (2008b). The shape of an i.v. pharmacokinetic profile of a compound is determined by the rates and extents of metabolism, distribution, EHR, and excretion. The parameters hepatic CLint, Kp factor, and kbil (determining hepatic metabolism, tissue distribution, and enterohepatic recirculation) were therefore modulated to get the best fit of the PBPK-simulated profile with the observed i.v. profile in the absence of renal and biliary excretion. These three parameters impact the line shape independent of each other. For example, distribution impacts the initial fall in concentration and the terminal phase of an i.v. profile, whereas a decrease or increase in CLint will displace the profile up or down, affecting its overall line shape very little. kbil impacts only the later phase of an i.v. profile. Thus, best-fit parameters are expected to be unique. If the fraction excreted unchanged in the urine (fe) is unknown, it is assumed that the compound has only hepatic clearance, as long as it is sufficiently lipophilic. If fe is known to be nonzero, the renal elimination rate constant, krenal, is modulated to reproduce the observed fe. The weighted squared residuals are minimized subject to variations in the mentioned parameters according to Eq. 10:Embedded Image(10)where Ci,observed and Ci,PBPKsimulated are the observed and PBPK-simulated concentrations, respectively, at same time point. The residual is weighted with the simulated concentration assuming that the variance is proportional to the concentrations. The predicted pharmacokinetic parameters for the best-fit profile such as area under the concentration-time profile (AUC), clearance (CL), and volume of distribution (Vd) matched with those observed. The absence of a good fit could be due to enterohepatic recirculation which leads to a higher than expected terminal concentrations in the observed profile. A good fit to the observed is then obtained by adjusting the first-order EHR rate constant.

When the best i.v. fit was obtained, the oral profile was simulated using the optimized values for CLint, Kp factor, and an EHR rate constant (where applicable), considering these to be invariant to the route of administration. Parameters affecting the oral profile are permeability, solubility, gastric emptying delay, and intestinal loss. Because compounds with good solubility and permeability are expected to show a complete absorption any observed reduction of the drug exposure (AUC) is likely to be due to intestinal loss. ISFs are modulated to minimize the weighted squared residuals as presented in Eq. 10, such that the model-simulated profile best fits the observed oral profile. The decision tree presented by Peters (2008b) has been used to analyze oral profile simulations with PBPK. For very low solubility compounds (nifedipine and tacrolimus), it was not possible to describe the upswing of the absorption phase using the measured solubility. In these cases, values that best described the initial upswing of the absorption phase were used. Indeed, it is well known that the conditions for an in vitro solubility experiment can be considerably different from those prevailing in vivo (Nicolaides et al., 1999). For compounds that cause an impairment of gastric emptying, an emptying rate that is lower than the average normal value has the effect of slowing the initial upswing of the absorption phase, but the terminal phase is characterized by higher than expected concentrations. Since intestinal loss, gastric emptying delay, and solubility impact different aspects of the oral PK profile, a unique set of best-fit parameters can be obtained. The intestinal availability corresponding to the best fit is taken as Fgr. Because the fraction absorbed (fa) is estimated by the program using measured solubility and permeability, the fraction escaping gut metabolism (fg) can also be estimated (Fg = fa × fg).

Estimation of Fg with the Indirect Method.

The traditional indirect method for estimating Fg uses hepatic availability (fh) and observed oral bioavailability (F) (Eqs. 11 and 12):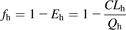Embedded Image(11)where Eh is hepatic extraction and Qh is the hepatic blood flow rate whose value is taken as 88.2 L/h in human and 1.2 L/h in rat, and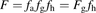Embedded Image(12)To estimate fg, fa is assumed to be 1, when an accurate measure of it is not available.

Assessment of Accuracy

Prediction accuracy was assessed with RMSE given by Eq. 13:Embedded Image(13)where predicted fg refers to fg derived from in vitro models or from rat in vivo models and observed fg refers to fg extracted by PBPK from human in vivo profiles.

Results

Comparisons of fg derived from different human in vitro systems have been made with fg extracted from human in vivo PK profiles using PBPK modeling. A comparison of fg extracted with PBPK from rat and human PK profiles is also reported.

Estimation of fg from In Vitro Systems.

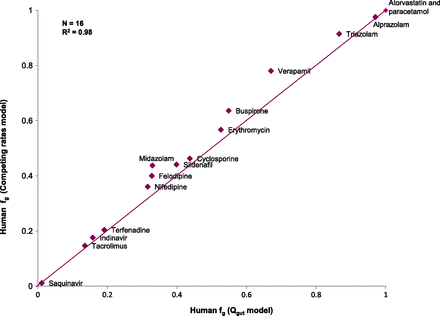
The relative rates of metabolism using expressed enzymes when scaled to the abundance of CYP3A4 in the liver showed a clear dominance of CYP3A4 contribution in the metabolism of the selected compounds, confirming the validity of using HLMs as a surrogate of CYP3A4-mediated intestinal metabolism for this dataset. Human intestinal clearance values for the selected compounds in the three different in vitro systems studied (HLM, intestinal S9 fraction, rCYP) are presented in Table 4. Figure 1 shows that fg estimates obtained from the competing rates model (Eq. 7) using intestinal S9 CLint,g compared well with those derived from the Qgut model (Eq. 2). A good agreement between both models (n = 16; RMSE = 0.057; R2=0.98) provided confidence in the use of the competing rate model (Eq. 7) to estimate human fg using CLint,g from in vitro systems. fg values derived from human in vitro systems as well as from human and rat in vivo PK profiles are presented in Table 5.

View this table:
TABLE 3

Pharmacokinetic data in humans and rats as used in the PBPK modeling

Rat and human PK data are from the literature (Supplemental Table 1).

View this table:
TABLE 4

Passive permeability (CLperm) and in vitro CLint from intestinal S9, HLM, and recombinant P450 and the scaled gut clearances (CLint,g) from HLM and rCYP

Fig. 1.
Fig. 1.

A comparison of fg derived from intestinal S9 using the Qgut and competing rates models.

View this table:
TABLE 5

Pharmacokinetic parameters, fraction of drug escaping intestinal metabolism (fg) derived from human in vitro systems using the model of competing rates (Eq. 7) and fg derived from in vivo pharmacokinetic profiles of rat and human

In vitro incubations in rat intestinal S9 preparations, freshly prepared in-house and obtained from commercial sources, did not produce significant substrate depletion over 60 minutes, and no in vitro CLint values were derived (data not shown). Although metabolite formation of hydroxymidazolam was detected in rat S9, any modifications to preparation procedures and incubation conditions did not recover reproducible substrate depletion comparable with human S9 material.

Extraction of Human fg from In Vivo PK Profiles Using PBPK.

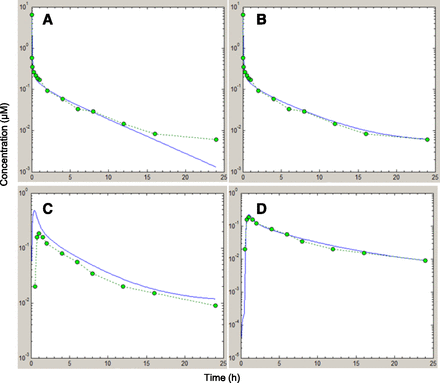
Figure 2 illustrates the PBPK simulation of human pharmacokinetic profile of midazolam, as an example. The i.v. profile of midazolam is simulated using the input data presented in Table 2. The Kp factor and intrinsic clearance are modulated until a best fit to the observed profile is obtained (Fig. 2A). The mismatch in the terminal phase is due to EHR. The biliary rate constant kbil is then adjusted until a best fit is observed (Fig. 2B). The parameters from this i.v. best fit are then employed for the oral profile simulation (Fig. 2C). The poor fit to the observed oral profile is due to intestinal loss and a possible lag time. The ISFs in the seven small intestinal and colonic compartments are then altered and a lag time of 30 minutes is introduced to get the best fit to the observed profile (Fig. 2D). The deviation from the default value of 1 in all of the small intestinal compartments suggests that there is a regional variation in the fg. Similarly, for all other compounds, the ISFs were adjusted to get the best fit to the observed profile. A good agreement between predicted and observed pharmacokinetic profiles guarantees an accurate estimation of fg. However, good fits were not obtained for all compounds. The poorest fit was obtained for triazolam (Supplemental Fig. 1). A possible explanation may lie in the existence of a nonlinear pathway in the range of 10−2 to 10−3 µM, which leads to a higher clearance at concentrations below 10−3 µM. For very low solubility compounds, such as nifedipine and tacrolimus, it was not possible to describe the upswing of the absorption phase using the measured solubility. In these cases, minimum in vivo solubility values that gave the best fit to the observed oral profile were used (170 and 70 µM for nifedipine and tacrolimus, respectively) after incorporating clearance and volume of distribution parameters extracted from fitting the i.v. profile. This is illustrated with nifedipine as an example (Supplemental Fig. 2). A reduction of gastric emptying rates was needed to simulate the PK profiles of verapamil (Supplemental Fig. 3). Saquinavir is a good example to demonstrate the value of the PBPK approach over the indirect method. PBPK simulations of saquinavir (Supplemental Fig. 4) show that a reduction in intrinsic clearance was needed in addition to a reduction in the ISFs for a good fit to be achieved. The i.v. best-fit intrinsic clearance was too high to simulate the oral profile, possibly due to saturation of hepatic uptake or metabolic clearance during oral administration, because the i.v. and oral doses are very different (12 and 600 mg, respectively). Because hepatic clearance affects the profile over the whole time course and gut metabolism affects only the absorption phase, it is possible to distinguish between the two with PBPK simulations. With the indirect method, the use of i.v. clearance exaggerates the role of hepatic extraction, leading to a large fg. The second peak in the oral profile for saquinavir after approximately 5 hours has been attributed to the intake of food, 4 hours after oral drug administration (Kupferschmidt et al., 1998). EHR of saquinavir is very unlikely since there is no such second peak in the intravenous profile. The inability to get a good fit in this case did not affect the estimation of fg to a great extent, because the AUC difference between the simulated and observed profiles is marginal. Alprazolam was fitted without any adjustments of intestinal loss. PBPK simulations in rats were also done similar to humans. As in humans, verapamil oral profiles were fitted with a reduced gastric emptying rate in rats.

Fig. 2.
Fig. 2.

PBPK simulations of midazolam in humans. The solid line represents PBPK simulation and markers represent observed data. (A) Best fit to observed i.v. PK profile of midazolam obtained by adjusting CLint and Kp factor. (B) The mismatch in the terminal phase due to EHR is addressed by using a first-order EHR rate constant that best fits the profile. (C) Simulated oral profile of midazolam using CLint, Kp factor, and EHR rate from i.v. best fit along with permeability and solubility. (D) Using a lag time of 30 minutes and reducing the ISFs from their default values of 1 in the seven small intestinal compartments and 0.1 in colon to 0.3, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, and 0.005 to account for intestinal loss provides a good fit to the observed oral profile.

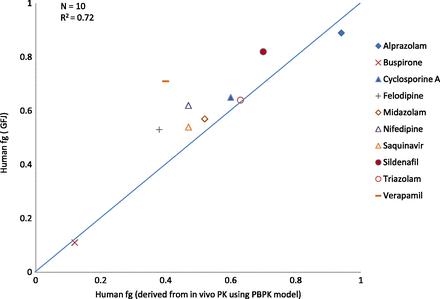
The fg values for humans and rats using PBPK simulations are presented in Table 5 along with literature-derived fg values for indirect method and a grapefruit juice (GFJ) approach (Gertz et al., 2008). In the GFJ approach, the intake of GFJ inhibits intestinal CYP3A without provoking hepatic interactions, thereby allowing discrimination between intestinal and hepatic clearances. Despite its limitations (Gertz et al., 2008), it is the only direct in vivo measure of human fg available. Human fg from the traditional indirect method and the PBPK approach have been compared with human fg from the GFJ method for the 10 compounds in which full i.v. and oral PK profiles were available. There is good agreement between the fg from PBPK and GFJ methods, with an RMSE of 0.12 (Fig. 3). The GFJ method provided higher fg values for felodipine, nifedipine, sildenafil, and verapamil. The RMSE for the same 10 compounds for fg from indirect and GFJ methods is 0.21. Thus, fg extracted by PBPK from human PK profiles was accepted as the best measure of human fg and was used to evaluate the in vitro models studied (intestinal S9, rCYP and HLM) and reported in the literature [human intestinal microsome (HIM)] as well as to evaluate rat fg extracted by PBPK from rat PK profiles.

Fig. 3.
Fig. 3.

A comparison of PBPK-derived fg with those from the GFJ method.

Evaluation of fg Derived from Human In Vitro Data and from Rat In Vivo PK Data as Models for Human fg.

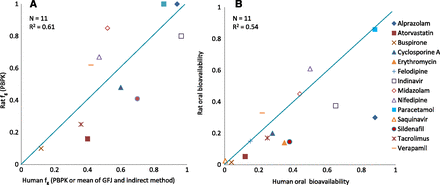
Validation of human in vitro systems has been done against the fg derived from PBPK simulations of human in vivo PK profiles. Figure 4 shows a comparative plot for the 11 test compounds that had fg values from all of the in vitro systems studied (intestinal S9, rCYP, and HLM) as well as in HIMs (Gertz et al., 2010). Ten of these 11 compounds had fg extracted by PBPK from human in vivo PK profiles. RMSE values for these 10 compounds are presented in Table 6. In general, all of the in vitro systems had comparable overall prediction performance, with RMSE ranging from 0.22 to 0.27. For the 14 compounds that had both human intestinal S9 and HIM data, RMSE was the same for both in vitro systems, against fg extracted from in vivo human PK profiles with PBPK simulations. However, fg extracted from in vivo rat PK profiles with PBPK simulations had the lowest RMSE (0.19) for the prediction of human fg (Fig. 5; Table 6). To summarize, all in vitro models evaluated are comparable in their ability to predict human fg. However, the rat fg is a better predictor of human fg.

Fig. 4.
Fig. 4.

A comparison of human fg values derived from in vitro systems using the model of competing rates with those derived from in vivo pharmacokinetic profiles using PBPK. Comparison of human fg derived from human S9 fraction, rCYP, HLM, and HIM (Gertz et al., 2010) with fg derived from PBPK.

View this table:
TABLE 6

Accuracy of predictions

Fig. 5.
Fig. 5.

A comparison of PBPK-derived fg (A) and systemic bioavailability (B) in rats and humans.

Discussion

This work presents a comparative overview of fg values derived from human and rat in vitro systems and validated against fg extracted from human pharmacokinetic profiles with a PBPK model for marketed drugs that are predominantly metabolized by CYP3A4.

fg from In Vivo Pharmacokinetic Profiles.

The GFJ method (Gertz et al., 2008) has been used to compare the fg from PBPK and indirect methods. The GFJ method assumes complete and selective inhibition of intestinal CYP3A, but additional inhibition of P-gp may explain the higher fg values with GFJ compared with PBPK (Fig. 3) for verapamil, nifedipine, and felodipine.

Human fg values derived from in vivo PK profiles using PBPK and indirect methods are usually similar (see Table 5) except for saquinavir. The PBPK method provides better estimates of fg compared with the indirect method for compounds with nonlinear PK in the therapeutic range. As illustrated with saquinavir, the indirect method may underestimate gut extraction when disregarding saturation of enzymes or uptake transporters at the higher hepatic concentrations after oral dosing. The indirect method provides a measure of intestinal availability, Fg, rather than fg, whereas PBPK modeling allows for estimation of fg, employing a calculated fa from solubility and permeability under physiologic conditions (Peters, 2008a). PBPK identifies in vivo solubility and therefore does not rely on in vitro solubility to predict fa. Because fa was assumed to be 1 for the estimation of fg with indirect method, the fg value for nifedipine (a compound whose absorption is limited by solubility) from indirect method compares well with that derived from PBPK. Nifedipine is a P-gp substrate but neither the PBPK nor the indirect method can distinguish between P-gp–mediated efflux and intestinal metabolism. P-gp–mediated intestinal efflux is often expected to be minimal due to high intestinal concentrations, especially for high-solubility drugs (Kwon et al., 2004; Cao et al., 2005) and a limited role of P-gp has been reported for cyclosporine A (Lee et al., 2005), tacrolimus (Saitoh et al., 2006), and verapamil (Cao et al., 2005).

PBPK simulations allow identification of regional variation in intestinal extraction, as demonstrated by variations in the ISFs along the gut to get the best fit to observed oral profile. This information can be important to assess the utility of extended release formulations to circumvent peak plasma concentrations arising from extensive jejunal metabolism. If metabolic extraction is extensive throughout the gut, or mediated by enzymes with high colonic abundance such as UGT2B7 and UGT2B15, an extended release formulation is unlikely to improve bioavailability. On the other hand, if metabolism is confined to the small intestinal region, like in CYP-mediated extraction, extended release formulations give the opportunity to improve gut bioavailability by targeting lower intestinal regions.

PBPK simulations can identify drug-induced gastric emptying delay (Peters, 2008a) as in the case of verapamil, which is known to delay gastric emptying (Yavorski et al., 1991). Gastric emptying delay may not impact fg but it has safety implications, because it reduces peak plasma concentrations by prolonging the absorption phase.

fg from In Vitro Systems.

Comparison of the model of competing rates (Eq. 7) and the Qgut model (Eq. 2) to obtain fg revealed that the Qgut model systematically predicts lower intestinal extraction from in vitro data. The average difference in fg was 0.04 and the highest difference was 0.11 for verapamil (Fig. 1). However, these differences appear marginal in the context of an experimental variation of up to 20%, thus justifying the use of Eq. 7.

Human fg values derived from all three in vitro systems correlate fairly well with fg derived from human in vivo pharmacokinetic profiles (Fig. 4). Conceptually, all three in vitro systems have their own strengths and limitations. Recombinant P450s and HLMs provide a convenient way to study P450-mediated metabolism, and provide phase I metabolism data without additional components of membrane permeation or phase II conjugations. Extended use of HLMs beyond the estimation of hepatic clearance to gut metabolism is justified only for compounds that are predominantly cleared by CYP3A4. Therefore, when CYP3A4 has been identified as the major metabolizing enzyme, HLM data can also be employed to compute the human gut clearance, and our results are in line with others (Gertz et al., 2010). However, phase II and cytosolic enzymes in the enterocyte is not reflected in microsomes or rCYPs. Therefore, intestinal S9 fractions provide a complement to the in vitro portfolio as they contain the membrane-bound enzymes of the FMO, CYP, and UGT families, often isolated as microsomal fractions, as well as all cytosolic enzymes such as esterases, amidases, hydrolases, SULTs, and GSTs (Jia and Liu, 2007). For CYP3A substrates, fg derived from human intestinal S9 and HIMs correlates equally well with in vivo fg. However, fg from human intestinal S9 fractions tends to be higher compared with that from HIM (Fig. 4) except for three compounds. This is in agreement with the literature showing that S9 fractions have a 3- to 4-fold lower P450 content than a microsome preparation (Jia and Liu, 2007). Such lower enzyme content per milligram of tissue preparation is usually compensated for with higher protein concentrations used in the in vitro incubation. The good agreement between human intestinal S9 and HLM derived estimates of the human fg of CYP3A substrates confirm the capability of S9 preparation to pick up the relevant reactions to a good extent. In contrast, subcellular preparations of rat intestine did not perform successfully in substrate depletion incubations. Neither rat intestinal S9 fractions obtained through different preparation methods (Bruyere et al., 2009) nor commercially available material produced reproducible compound turnover of the test compounds. Modifications of incubation conditions from phosphate buffers as used for human material to Tris buffers, with varied magnesium supplementation were also unsuccessful. This observation, although mechanistically unexplained, is in agreement with observations from other groups who also report that rat intestinal preparations show lower metabolite yields or less compound depletion than human preparations (van de Kerkhof et al., 2007; Komura and Iwaki, 2011; Bueters et al., 2013). The neglect of unbound fractions in vitro may affect the accuracy estimated of fg, particularly the lipophilic drugs felodipine, saquinavir, and tacrolimus, because nonspecific binding is correlated to lipophilicity (Austin et al., 2002).

Rat as a Model for CYP3A-Mediated Intestinal Metabolism in Human.

Preclinical species have been shown to be poor predictors of human bioavailability (Sietsema, 1989; Grass et al., 2002; Cao et al., 2006; Mitschke et al., 2008). It is also claimed that intestinal metabolism does not correlate between species (Takahashi et al., 2009; Akabane et al., 2010; Bueters et al., 2013). This lack of correlation is attributable to large species differences in the isoforms and expression levels of major intestinal drug-metabolizing enzymes such as P450s, UGTs, and SULTs (Glatt et al., 2001; Bock et al., 2002; Mackenzie et al., 2005; Mizuma et al., 2005; Ritter, 2007; van de Kerkhof et al., 2007; Komura and Iwaki, 2011). CYP3A9 is considered the ortholog of human CYP3A4 in the rat and the most abundant isoform in male rat intestine, whereas the female rat shows a preference of CYP3A62. CYP2C6 and CYP2C11 are additional CYP isoforms in the rat (Komura and Iwaki, 2011). Our study, however, shows a fairly good correlation between rat and human fg derived from the in vivo profiles of CYP3A substrates. In fact, the rat fg is associated with a lower RMSE (0.19) compared with fg derived from human in vitro systems (RMSE = 0.22–0.27). One possible explanation may be that compounds with high absorption rate constants have minimal contact with intestinal enzymes. For CYP3A (a low-affinity, high-capacity enzyme), this implies that differences in isoforms and enzyme abundances between the two species are likely to play a limited role. Intestinal availability of CYP3A substrates in humans have been shown to be closest to that in rats compared with other common preclinical species such as mice, dogs, and monkeys (Komura and Iwaki, 2008). The rat is also a good model for the human fraction absorbed (Cao et al., 2006). We therefore conclude that for compounds predominantly metabolized by CYP3A, the rat fg provides a reliable prediction of intestinal extraction in humans when the compounds have high fa (close to 1). For compounds that are additionally metabolized by CYP2C isoforms, a higher intestinal extraction may be observed in the rat, especially for compounds with lower permeability.

In conclusion, there is little risk of losing accuracy by employing the model of competing rates (Eq. 2) to estimate fg. Use of the PBPK method is preferable over the indirect method for deriving fg for compounds with nonlinear PK or having fa significantly < 1. In addition, PBPK simulations allow identification of regional variation in intestinal availability. The in vitro systems evaluated in this study were comparable in their predictive performance and the choice of method needs to be guided by type of metabolism, contribution of CYP3A to overall metabolism, and development stage. Finally, rat fg provides reliable prediction of intestinal extraction for compounds predominantly metabolized by CYP3A in humans.

Acknowledgments

The authors thank Åsa Sjöberg for skillful technical assistance with preparation of the biological systems, Drs. Mareike Lutz and Lena Brive for scientific support with the bioanalysis, and Anna-Lena Ungell for support.

Authorship Contributions

Participated in research design: Hilgendorf, Dolgos, Peters.

Conducted experiments: Karlsson, Bouchene.

Performed data analysis: Karlsson, Bouchene.

Wrote or contributed to the writing of the manuscript: Karlsson, Bouchene, Hilgendorf, Dolgos, Peters.

Footnotes

    • Received February 27, 2013.
    • Accepted August 5, 2013.

  • ↵1 Current affiliation: Chalmers University of Technology, Gothenburg, Sweden.

  • ↵2 Current affiliation: Uppsala University, Uppsala, Sweden.

  • ↵3 Current affiliation: Merck KGaA, Darmstadt, Germany.

  • dx.doi.org/10.1124/dmd.113.051664.

  • ↵Embedded ImageThis article has supplemental material available at dmd.aspetjournals.org.

Abbreviations

ACN
acetonitrile
AUC
area under the concentration-time profile
CL
clearance
CLint,g
intrinsic clearance in the gut
EHR
enterohepatic recirculation
F
bioavailability
Fg
intestinal availability
fg
fraction escaping gut metabolism
fu,p
fraction unbound in plasma
GFJ
grapefruit juice
HIM
human intestinal microsome
HLM
human liver microsome
ISF
intestinal scaling factor
P-gp
P-glycoprotein
P450
cytochrome P450
PBPK
physiologically-based pharmacokinetics
PK
pharmacokinetics
rCYP
recombinant cytochrome P450
RMSE
root mean square error
UGT
uridine 5′-diphospho-glucuronosyltransferase
Vd
volume of distribution

References

  1. ↵
    1. Akabane T,
    2. Tabata K,
    3. Kadono K,
    4. Sakuda S,
    5. Terashita S, and
    6. Teramura T
    (2010) A comparison of pharmacokinetics between humans and monkeys. Drug Metab Dispos 38:308–316.
    OpenUrlAbstract/FREE Full Text
  2. ↵
    1. Austin RP,
    2. Barton P,
    3. Cockroft SL,
    4. Wenlock MC, and
    5. Riley RJ
    (2002) The influence of nonspecific microsomal binding on apparent intrinsic clearance, and its prediction from physicochemical properties. Drug Metab Dispos 30:1497–1503.
    OpenUrlAbstract/FREE Full Text
  3. ↵
    1. Benet LZ,
    2. Cummins CL, and
    3. Wu CY
    (2004) Unmasking the dynamic interplay between efflux transporters and metabolic enzymes. Int J Pharm 277:3–9.
    OpenUrlCrossRefPubMed
  4. ↵
    1. Benet LZ,
    2. Izumi T,
    3. Zhang Y,
    4. Silverman JA, and
    5. Wacher VJ
    (1999) Intestinal MDR transport proteins and P-450 enzymes as barriers to oral drug delivery. J Control Release 62:25–31.
    OpenUrlCrossRefPubMed
  5. ↵
    1. Bock KW,
    2. Bock-Hennig BS,
    3. Münzel PA,
    4. Brandenburg JO,
    5. Köhle CT,
    6. Soars MG,
    7. Riley RJ,
    8. Burchell B,
    9. von Richter O,
    10. Eichelbaum MF,
    11. et al.
    (2002) Tissue-specific regulation of canine intestinal and hepatic phenol and morphine UDP-glucuronosyltransferases by beta-naphthoflavone in comparison with humans. Biochem Pharmacol 63:1683–1690.
    OpenUrlCrossRefPubMed
  6. ↵
    1. Bruyère A,
    2. Declevès X,
    3. Bouzom F,
    4. Proust L,
    5. Martinet M,
    6. Walther B, and
    7. Parmentier Y
    (2009) Development of an optimized procedure for the preparation of rat intestinal microsomes: comparison of hepatic and intestinal microsomal cytochrome P450 enzyme activities in two rat strains. Xenobiotica 39:22–32.
    OpenUrlCrossRefPubMed
  7. ↵
    1. Bueters T,
    2. Juric S,
    3. Sohlenius-Sternbeck AK,
    4. Hu Y, and
    5. Bylund J
    (2013) Rat poorly predicts the combined non-absorbed and presystemically metabolized fractions in the human. Xenobiotica 43:607–616.
    OpenUrlCrossRefPubMed
  8. ↵
    1. Cao X,
    2. Gibbs ST,
    3. Fang L,
    4. Miller HA,
    5. Landowski CP,
    6. Shin HC,
    7. Lennernas H,
    8. Zhong Y,
    9. Amidon GL,
    10. Yu LX,
    11. et al.
    (2006) Why is it challenging to predict intestinal drug absorption and oral bioavailability in human using rat model. Pharm Res 23:1675–1686.
    OpenUrlCrossRefPubMed
  9. ↵
    1. Cao X,
    2. Yu LX,
    3. Barbaciru C,
    4. Landowski CP,
    5. Shin HC,
    6. Gibbs S,
    7. Miller HA,
    8. Amidon GL, and
    9. Sun D
    (2005) Permeability dominates in vivo intestinal absorption of P-gp substrate with high solubility and high permeability. Mol Pharm 2:329–340.
    OpenUrlCrossRefPubMed
  10. ↵
    1. Court MH,
    2. Zhang X,
    3. Ding X,
    4. Yee KK,
    5. Hesse LM, and
    6. Finel M
    (2012) Quantitative distribution of mRNAs encoding the 19 human UDP-glucuronosyltransferase enzymes in 26 adult and 3 fetal tissues. Xenobiotica 42:266–277.
    OpenUrlCrossRefPubMed
  11. ↵
    1. Galetin A,
    2. Gertz M, and
    3. Houston JB
    (2008) Potential role of intestinal first-pass metabolism in the prediction of drug-drug interactions. Expert Opin Drug Metab Toxicol 4:909–922.
    OpenUrlCrossRefPubMed
  12. ↵
    1. Gammans RE,
    2. Mayol RF, and
    3. LaBudde JA
    (1986) Metabolism and disposition of buspirone. Am J Med 80 (3B):41–51.
    OpenUrlPubMed
  13. ↵
    1. Gertz M,
    2. Davis JD,
    3. Harrison A,
    4. Houston JB, and
    5. Galetin A
    (2008) Grapefruit juice-drug interaction studies as a method to assess the extent of intestinal availability: utility and limitations. Curr Drug Metab 9:785–795.
    OpenUrlCrossRefPubMed
  14. ↵
    1. Gertz M,
    2. Harrison A,
    3. Houston JB, and
    4. Galetin A
    (2010) Prediction of human intestinal first-pass metabolism of 25 CYP3A substrates from in vitro clearance and permeability data. Drug Metab Dispos 38:1147–1158.
    OpenUrlAbstract/FREE Full Text
  15. ↵
    1. Gertz M,
    2. Houston JB, and
    3. Galetin A
    (2011) Physiologically based pharmacokinetic modeling of intestinal first-pass metabolism of CYP3A substrates with high intestinal extraction. Drug Metab Dispos 39:1633–1642.
    OpenUrlAbstract/FREE Full Text
  16. ↵
    1. Glatt H,
    2. Boeing H,
    3. Engelke CE,
    4. Ma L,
    5. Kuhlow A,
    6. Pabel U,
    7. Pomplun D,
    8. Teubner W, and
    9. Meinl W
    (2001) Human cytosolic sulphotransferases: genetics, characteristics, toxicological aspects. Mutat Res 482:27–40.
    OpenUrlCrossRefPubMed
  17. ↵
    1. Goldin BR
    (1990) Intestinal microflora: metabolism of drugs and carcinogens. Ann Med 22:43–48.
    OpenUrlPubMed
  18. ↵
    Goodman L, Gilman A, Brunton LL, Lazo JS, Parker KL (2006) Goodman & Gilman's the Pharmacological Basis of Therapeutics, McGraw-Hill Companies, Inc., New York.
  19. ↵
    1. Grass S,
    2. Xu IS,
    3. Wiesenfeld-Hallin Z, and
    4. Xu XJ
    (2002) Comparison of the effect of intrathecal endomorphin-1 and endomorphin-2 on spinal cord excitability in rats. Neurosci Lett 324:197–200.
    OpenUrlCrossRefPubMed
  20. ↵
    1. Hellriegel ET,
    2. Bjornsson TD, and
    3. Hauck WW
    (1996) Interpatient variability in bioavailability is related to the extent of absorption: implications for bioavailability and bioequivalence studies. Clin Pharmacol Ther 60:601–607.
    OpenUrlCrossRefPubMed
  21. ↵
    1. Jia L and
    2. Liu X
    (2007) The conduct of drug metabolism studies considered good practice (II): in vitro experiments. Curr Drug Metab 8:822–829.
    OpenUrlCrossRefPubMed
  22. ↵
    1. Kadono K,
    2. Akabane T,
    3. Tabata K,
    4. Gato K,
    5. Terashita S, and
    6. Teramura T
    (2010) Quantitative prediction of intestinal metabolism in humans from a simplified intestinal availability model and empirical scaling factor. Drug Metab Dispos 38:1230–1237.
    OpenUrlAbstract/FREE Full Text
  23. ↵
    1. Kaminsky LS and
    2. Zhang QY
    (2003) The small intestine as a xenobiotic-metabolizing organ. Drug Metab Dispos 31:1520–1525.
    OpenUrlFREE Full Text
  24. ↵
    1. Komura H and
    2. Iwaki M
    (2008) Species differences in in vitro and in vivo small intestinal metabolism of CYP3A substrates. J Pharm Sci 97:1775–1800.
    OpenUrlCrossRefPubMed
  25. ↵
    1. Komura H and
    2. Iwaki M
    (2011) In vitro and in vivo small intestinal metabolism of CYP3A and UGT substrates in preclinical animals species and humans: species differences. Drug Metab Rev 43:476–498.
    OpenUrlCrossRefPubMed
  26. ↵
    1. Kupferschmidt HH,
    2. Fattinger KE,
    3. Ha HR,
    4. Follath F, and
    5. Krähenbühl S
    (1998) Grapefruit juice enhances the bioavailability of the HIV protease inhibitor saquinavir in man. Br J Clin Pharmacol 45:355–359.
    OpenUrlCrossRefPubMed
  27. ↵
    1. Kwon H,
    2. Lionberger RA, and
    3. Yu LX
    (2004) Impact of P-glycoprotein-mediated intestinal efflux kinetics on oral bioavailability of P-glycoprotein substrates. Mol Pharm 1:455–465.
    OpenUrlCrossRefPubMed
  28. ↵
    1. Lee YJ,
    2. Chung SJ, and
    3. Shim CK
    (2005) Limited role of P-glycoprotein in the intestinal absorption of cyclosporin A. Biol Pharm Bull 28:760–763.
    OpenUrlCrossRefPubMed
  29. ↵
    1. Mackenzie PI,
    2. Gregory PA,
    3. Lewinsky RH,
    4. Yasmin SN,
    5. Height T,
    6. McKinnon RA, and
    7. Gardner-Stephen DA
    (2005) Polymorphic variations in the expression of the chemical detoxifying UDP glucuronosyltransferases. Toxicol Appl Pharmacol 207 (Suppl):77–83.
    OpenUrlCrossRefPubMed
  30. ↵
    1. Markwell MA,
    2. Haas SM,
    3. Bieber LL, and
    4. Tolbert NE
    (1978) A modification of the Lowry procedure to simplify protein determination in membrane and lipoprotein samples. Anal Biochem 87:206–210.
    OpenUrlCrossRefPubMed
  31. ↵
    1. Mitschke D,
    2. Reichel A,
    3. Fricker G, and
    4. Moenning U
    (2008) Characterization of cytochrome P450 protein expression along the entire length of the intestine of male and female rats. Drug Metab Dispos 36:1039–1045.
    OpenUrlAbstract/FREE Full Text
  32. ↵
    1. Mizuma T,
    2. Kawashima K,
    3. Sakai S,
    4. Sakaguchi S, and
    5. Hayashi M
    (2005) Differentiation of organ availability by sequential and simultaneous analyses: intestinal conjugative metabolism impacts on intestinal availability in humans. J Pharm Sci 94:571–575.
    OpenUrlCrossRefPubMed
  33. ↵
    1. Nicolaides E,
    2. Galia E,
    3. Efthymiopoulos C,
    4. Dressman JB, and
    5. Reppas C
    (1999) Forecasting the in vivo performance of four low solubility drugs from their in vitro dissolution data. Pharm Res 16:1876–1882.
    OpenUrlCrossRefPubMed
  34. ↵
    1. Obach RS,
    2. Lombardo F, and
    3. Waters NJ
    (2008) Trend analysis of a database of intravenous pharmacokinetic parameters in humans for 670 drug compounds. Drug Metab Dispos 36:1385–1405.
    OpenUrlAbstract/FREE Full Text
  35. ↵
    1. Ohno S and
    2. Nakajin S
    (2009) Determination of mRNA expression of human UDP-glucuronosyltransferases and application for localization in various human tissues by real-time reverse transcriptase-polymerase chain reaction. Drug Metab Dispos 37:32–40.
    OpenUrlAbstract/FREE Full Text
  36. ↵
    1. Paine MF,
    2. Hart HL,
    3. Ludington SS,
    4. Haining RL,
    5. Rettie AE, and
    6. Zeldin DC
    (2006) The human intestinal cytochrome P450 “pie”. Drug Metab Dispos 34:880–886.
    OpenUrlAbstract/FREE Full Text
  37. ↵
    1. Paine MF,
    2. Khalighi M,
    3. Fisher JM,
    4. Shen DD,
    5. Kunze KL,
    6. Marsh CL,
    7. Perkins JD, and
    8. Thummel KE
    (1997) Characterization of interintestinal and intraintestinal variations in human CYP3A-dependent metabolism. J Pharmacol Exp Ther 283:1552–1562.
    OpenUrlAbstract/FREE Full Text
  38. ↵
    1. Peters SA
    (2008a) Evaluation of a generic physiologically based pharmacokinetic model for lineshape analysis. Clin Pharmacokinet 47:261–275.
    OpenUrlCrossRefPubMed
  39. ↵
    1. Peters SA
    (2008b) Identification of intestinal loss of a drug through physiologically based pharmacokinetic simulation of plasma concentration-time profiles. Clin Pharmacokinet 47:245–259.
    OpenUrlCrossRefPubMed
  40. ↵
    1. Peters SA,
    2. Schroeder PE,
    3. Giri N, and
    4. Dolgos H
    (2012) Evaluation of the use of static and dynamic models to predict drug-drug interaction and its associated variability: impact on drug discovery and early development. Drug Metab Dispos 40:1495–1507.
    OpenUrlAbstract/FREE Full Text
  41. ↵
    1. Ritter JK
    (2007) Intestinal UGTs as potential modifiers of pharmacokinetics and biological responses to drugs and xenobiotics. Expert Opin Drug Metab Toxicol 3:93–107.
    OpenUrlCrossRefPubMed
  42. ↵
    1. Rodgers T,
    2. Leahy D, and
    3. Rowland M
    (2005) Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J Pharm Sci 94:1259–1276.
  43. ↵
    1. Rodgers T and
    2. Rowland M
    (2006) Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci 95:1238–1257.
    OpenUrlCrossRefPubMed
  44. ↵
    1. Rowland M,
    2. Benet LZ, and
    3. Graham GG
    (1973) Clearance concepts in pharmacokinetics. J Pharmacokinet Biopharm 1:123–136.
    OpenUrlCrossRefPubMed
  45. ↵
    1. Saitoh H,
    2. Saikachi Y,
    3. Kobayashi M,
    4. Yamaguchi M,
    5. Oda M,
    6. Yuhki Y,
    7. Achiwa K,
    8. Tadano K,
    9. Takahashi Y, and
    10. Aungst BJ
    (2006) Limited interaction between tacrolimus and P-glycoprotein in the rat small intestine. Eur J Pharm Sci 28:34–42.
    OpenUrlCrossRefPubMed
  46. ↵
    1. Sietsema WK
    (1989) The absolute oral bioavailability of selected drugs. Int J Clin Pharmacol Ther Toxicol 27:179–211.
    OpenUrlPubMed
  47. ↵
    1. Siissalo S and
    2. Heikkinen AT
    (2013) In vitro methods to study the interplay of drug metabolism and efflux in the intestine. Curr Drug Metab 14:102–111.
    OpenUrlCrossRefPubMed
  48. ↵
    1. Sjöberg Å,
    2. Lutz M,
    3. Tannergren C,
    4. Wingolf C,
    5. Borde A, and
    6. Ungell AL
    (2013) Comprehensive study on regional human intestinal permeability and prediction of fraction absorbed of drugs using the Ussing chamber technique. Eur J Pharm Sci 48:166–180.
    OpenUrlCrossRefPubMed
  49. ↵
    1. Takahashi M,
    2. Washio T,
    3. Suzuki N,
    4. Igeta K, and
    5. Yamashita S
    (2009) The species differences of intestinal drug absorption and first-pass metabolism between cynomolgus monkeys and humans. J Pharm Sci 98:4343–4353.
    OpenUrlCrossRefPubMed
  50. ↵
    1. Taketani M,
    2. Shii M,
    3. Ohura K,
    4. Ninomiya S, and
    5. Imai T
    (2007) Carboxylesterase in the liver and small intestine of experimental animals and human. Life Sci 81:924–932.
    OpenUrlCrossRefPubMed
  51. ↵
    1. Thelen K and
    2. Dressman JB
    (2009) Cytochrome P450-mediated metabolism in the human gut wall. J Pharm Pharmacol 61:541–558.
    OpenUrlCrossRefPubMed
  52. ↵
    1. van de Kerkhof EG,
    2. de Graaf IA, and
    3. Groothuis GM
    (2007) In vitro methods to study intestinal drug metabolism. Curr Drug Metab 8:658–675.
    OpenUrlCrossRefPubMed
  53. ↵
    1. van de Kerkhof EG,
    2. Ungell AL,
    3. Sjöberg AK,
    4. de Jager MH,
    5. Hilgendorf C,
    6. de Graaf IA, and
    7. Groothuis GM
    (2006) Innovative methods to study human intestinal drug metabolism in vitro: precision-cut slices compared with ussing chamber preparations. Drug Metab Dispos 34:1893–1902.
    OpenUrlAbstract/FREE Full Text
  54. ↵
    1. Winiwarter S,
    2. Bonham NM,
    3. Ax F,
    4. Hallberg A,
    5. Lennernäs H, and
    6. Karlén A
    (1998) Correlation of human jejunal permeability (in vivo) of drugs with experimentally and theoretically derived parameters. A multivariate data analysis approach. J Med Chem 41:4939–4949.
    OpenUrlCrossRefPubMed
  55. ↵
    1. Wishart DS,
    2. Knox C,
    3. Guo AC,
    4. Cheng D,
    5. Shrivastava S,
    6. Tzur D,
    7. Gautam B, and
    8. Hassanali M
    (2008) DrugBank: a knowledgebase for drugs, drug actions and drug targets. Nucleic Acids Res 36 (Database issue):D901–D906.
    OpenUrlAbstract/FREE Full Text
  56. ↵
    1. Yang J,
    2. Jamei M,
    3. Yeo KR,
    4. Tucker GT, and
    5. Rostami-Hodjegan A
    (2007) Prediction of intestinal first-pass drug metabolism. Curr Drug Metab 8:676–684.
    OpenUrlCrossRefPubMed
  57. ↵
    1. Yavorski RT,
    2. Hallgren SE, and
    3. Blue PW
    (1991) Effects of verapamil and diltiazem on gastric emptying in normal subjects. Dig Dis Sci 36:1274–1276.
    OpenUrlCrossRefPubMed
  58. ↵
    1. Zahir H,
    2. Nand RA,
    3. Brown KF,
    4. Tattam BN, and
    5. McLachlan AJ
    (2001) Validation of methods to study the distribution and protein binding of tacrolimus in human blood. J Pharmacol Toxicol Methods 46:27–35.
    OpenUrlCrossRefPubMed
Back to top

In this issue

Download PDF
Article Alerts
Email Article
Citation Tools

Research ArticleSpecial Section on Prediction of Human Pharmacokinetic Parameters from In Vitro Systems

Prediction of Human Intestinal First-Pass Metabolism

Fredrik H. Karlsson, Salim Bouchene, Constanze Hilgendorf, Hugues Dolgos and Sheila Annie Peters
Drug Metabolism and Disposition December 1, 2013, 41 (12) 2033-2046; DOI: https://doi.org/10.1124/dmd.113.051664
Twitter logo Facebook logo Mendeley logo

Jump to section

Advertisement