Experimental Procedures

Materials.

Compounds A and B and all internal standards were obtained from Pfizer's proprietary sample bank (Groton, CT). The physiochemical properties of these two compounds are reported in Table1. All compounds were >99% pure, as determined by high-pressure liquid chromatography. Pooled human liver microsomes (n > 56) were obtained from an in-house bank of liver microsomes maintained at Pfizer Global Research and Development (Groton, CT). Microsomal CYP content, estimated as described previously (Omura and Sato, 1964), was 0.43 nmol/mg of protein. Solvents and other reagents were obtained from common sources and were of reagent grade or better. NADPH (97% purity) was obtained from Sigma Chemical Co. (St. Louis, MO).

Theoretical Impact of Microsomal Concentration on Free Fraction.

Assuming equilibrium kinetics and nonsaturable binding, the relationship between free fraction (fu_mic), dissociation constant (K_d), and binding component concentration (B) can be written in a manner consistent with that previously described in the literature (Romer and Bickel, 1979).fumic=Kd[B]+Kd Equation 1Using eq. 1 to define the ratio of free fractions expected at two different concentrations of nonspecific binding components, [B₁] and [B₂], we obtain eq. 2.fumic,1fumic,2=[B2]+Kd[B1]+Kd Equation 2Close examination of eq. 2 reveals two distinct possibilities for the effect of nonspecific binding components on free fraction. When the concentrations of these components are much less thanK_d, the fraction unbound is expected to be constant. When the concentrations of these components are much greater than K_d, the change in free fraction is expected to be inversely proportional to the changes in their concentration.

Theoretical Impact of Microsomal Concentration on Half-Life.

Assuming that only free substrate fu_mic · [S] is able to be acted upon by enzyme [E], and V_max is expressed in terms of a catalysis rate constant (k_cat) and the total mass of enzyme (E_total), the velocity (v) is defined in eq. 3 by the Michaelis-Menten equation.v=Etotal·kcat·[S]·fumicKm+[S]·fumic Equation 3Assuming first order conditions (i.e.,K_m ≫ fu_mic · [S]) and expressing velocity in terms of half-life (t_1/2) and total mass of substrate (S_total), one obtains eq. 4.v=ln(2)·Stotalt1/2 Equation 4Substituting eq. 3 for velocity and simplifying, one obtains eq.5. It should be noted that eq. 5 represents an illustration of the factors that influence half-life under the assumed conditions, not the method by which V_max andK_m were determined.t1/2=ln(2)·Stotal·KmEtotal·kcat·[S]·fumic Equation 5Taking the ratio of half-life at two different enzyme concentrations [E₁] and [E₂], one obtains eq. 6.t1/2,1t1/2,2=[E2][E1]·fumic,1fumic,2 Equation 6Substituting eq. 2 for the ratio of fu_mic,1 and fu_mic,2 and simplifying, one obtains eq. 7.t1/2,1t1/2,2=[E2][E1]·[B1]+Kd[B2]+Kd Equation 7It is important to note that, in the current examination, the concentrations of enzyme and nonspecific binding components are altered concurrently. Under these conditions, close examination of eq. 7reveals two distinct possibilities for the effect of nonspecific binding components on half-life. When the concentrations of these components are much less than K_d, the half-life is expected to be inversely proportional to the simultaneous changes with enzyme concentration. When the concentrations of these components are much greater than K_d, half-life is expected to be independent of simultaneous changes with enzyme concentration.

Theoretical Impact of Microsomal Concentration onK_m.

The definition of apparent K_m is provided in eq. 8.Km,app=Kmfumic Equation 8The ratio of apparent K_m determined at two different microsomal concentrations is defined in eq. 9.Km1,appKm2,app=fumic,2fumic,1=[B1]+Kd[B2]+Kd Equation 9Close examination of eq. 9 reveals two distinct possibilities for the effect for the effect of nonspecific binding components on apparent K_m. When the concentrations of these components are much less than K_d, the apparent K_m is expected to be constant. When the concentrations of these components are much greater thanK_d, the apparentK_m is expected to be proportional to simultaneous changes with enzyme concentration.

Metabolic Incubations.

The microsomal clearances of compounds A and B were examined in pooled human liver microsomes at total protein concentrations of 0.46 and 2.3 mg/ml, corresponding to total CYP concentrations of 0.20 and 1.0 μM, respectively. These concentrations were achieved through dilution of a stock suspension of microsomes with sodium phosphate buffer (pH 7.4, 100 mM) to assure a 5-fold difference in the concentration of all nonspecific binding components. Selected substrate concentrations (0.1–300 μM) were incubated with magnesium chloride (5 mM) and NADPH (2 mM) in 0.75 ml of sodium phosphate buffer (pH 7.4, 100 mM) at 37°C. Microsomes were preincubated for approximately 5 min before the reaction was initiated by the addition of NADPH. Aliquots of 100 μl were removed from the incubations at 0, 5, 10, 15, 30, and 45 min and added to 100 μl of acetonitrile to terminate further metabolism. All incubations were conducted in triplicate.

Equilibrium Dialysis.

Compounds A and B (3.0 μM) were mixed with the indicated pooled human liver microsomes suspended in magnesium chloride (5 mM) and sodium phosphate buffer (pH 7.4, 100 mM). The mixture (1.0 ml) was subject to equilibrium dialysis versus 1.0 ml of sodium phosphate buffer (pH 7.4, 100 mM) at 37°C using a Spectrum semi-micro apparatus (Spectrum Industries, Los Angeles, CA) and Spectra-Por no.2 membranes with molecular weight cutoff of 12 to 14 kDa. Equilibrium was achieved by rotating the cells at 25 rpm for 4.5 h (Obach, 1997). All experiments were performed in triplicate.

High-Pressure Liquid Chromatography Analysis.

Quantitation of compound A was accomplished using an LC-MS assay. Samples were injected (1–5 μl; HTSPal Autosampler, CTC Analytics, Carrboro, NC) onto a Primesphere 2.0- × 30-mm 5-μm C₁₈ column (Phenomenex, Torrance, CA) with a run time of 2.0 min. Analytes were eluted with acetonitrile/ammonium acetate (pH 6.8, 10 mM)/isopropanol (60:39:1, v/v/v) at a flow rate of 0.550 ml/min produced by a Shimadzu LC-10ADVP binary pump (Shimadzu, Kyoto, Japan). From 0.4 to 2.0 min the entire column effluent entered the Turbo Ionspray source (500°C, 7 liters/min nitrogen) of a PE-Sciex API-150 single quadrupole mass spectrometer (Concord, ON, Canada). Compound A and the internal standard were measured using single ion monitoring (m/z = 442.2 and 480.2, respectively) with positive ionization at a retention time of 0.7 min.

Quantitation of compound B was accomplished using an LC-MS/MS assay. Samples were injected (1–5 μl; HTSPal Autosampler) onto a monitor 3.0- × 30-mm 3-μM C₁₈ column (Column Engineering, Ontario, Canada) maintained a 37°C with a run time of 4.5 min. Analytes were eluted with a high-pressure linear gradient program consisting of methanol (“A”) and ammonium acetate (pH 6.8, 10 mM)/isopropanol (99:1, v/v) (“B”) produced by two Shimadzu LC-10ADVP binary pumps and a 10-μl static mixer with a combined flow rate of 0.300 ml/min. An initial concentration of 20% A was immediately ramped to 100% A in 3 min and held for 0.5 min. The system was returned to the initial conditions in a single step and allowed to equilibrate for 1 min. From 1.5 to 4.0 min the entire column effluent entered the Turbo Ionspray source (500°C, 8 liters/min nitrogen) of a PE-Sciex API-3000 triple quadrupole mass spectrometer. Compound B and the internal standard were measured using multiple reaction monitoring (m/z = 411.2–339.2 and 466.1–380.1, respectively) with negative ionization at a retention time of 2.3 and 2.4 min, respectively.

Standard curves were used for analysis of equilibrium dialysis, and microsomal incubation samples were used for enzyme kinetic calculations. Equilibrium dialysis samples were prepared by mixing microsome samples with control buffer or buffer samples with control microsomes to yield an identical matrix, which were combined with internal standard in acetonitrile to precipitate proteins prior to analysis of supernatant. Samples from microsomal incubations were vortexed and centrifuged, and an aliquot of supernatant was combined with internal standard for analysis.

Calculations.

The initial reaction velocity (v₀) was calculated by multiplying the nominal substrate concentration at time 0 ([S]₀) by the slope of the log-linear regression from the concentration versus time relationship (k) and dividing by the protein concentration of the incubation, v₀ = −k · [S]₀/[P]. The velocity data were plotted in double reciprocal and Eadie-Hofstee plots to confirm enzyme kinetics consistent with a single metabolic site. Apparent K_m andV_max were estimated by modeling velocity versus substrate concentration using the Michaelis-Menten equation and WinNonlin 2.1 (Pharsight Inc., Palo Alto, CA). In contrast, microsomal half-lives were calculated using the slope of the log-linear regression from the concentration versus time relationship (k),t_1/2 = −ln(2)/k. Consistent with the required assumptions outlined in the theoretical section, half-life was reported for the lowest concentration examined (such that S ≪ K_m). Intrinsic clearance was calculated from half-life using the following formula (Obach et al., 1997).CLint,app=0.693in vitro t1/2·ml incubationmg microsomes·45 mg microsomeg liver·20 g liverkg per body weight

Results

Effect of Microsomal Concentration on Free Fraction (Table 2).

A 5-fold increase in microsomal concentration was associated with an equivalent 5-fold decrease in free fraction of compound A (high nonspecific binding) from 0.055 to 0.012 (Table2). In contrast, the free fraction of compound B (low nonspecific binding) was not proportionally influenced by microsomal concentration (Table 2).

Effect of Microsomal Concentration on Half-Life and CL_int,app (Table 2).

The half-life of compound A was independent of microsomal concentration. In this case, the decrease in CL_int,app from 80 to 17 ml/min/kg was proportional to the increase in microsomal concentration. For compound B, the 5-fold increase in microsomal concentration was associated with a decrease in half-life from 19 to 5.9 min. In this case, there was no proportional change in CL_int,app. Correction of CL_int,app for the free fraction yielded estimates that were independent of microsomal concentration for both compounds.

Effect of Microsomal Concentration onK_m,app.

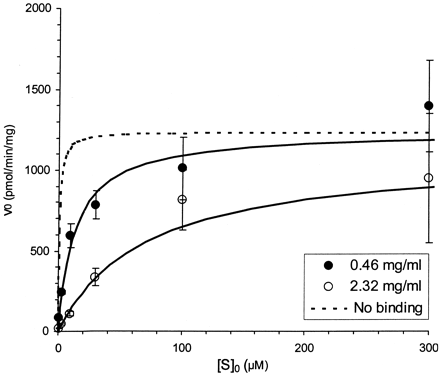
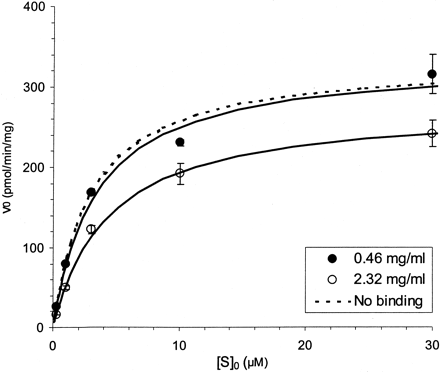
The K_m,app of compound A increased proportionally to the 5-fold increase in microsomal concentration. In this case, a 5-fold increase in microsomal concentration was associated with an equivalent increase in K_m,app from 13 to 70 μM (Fig. 1, Table 2). In contrast, the K_m,app of compound B was not proportionally influenced by changes in microsomal concentration (Fig.2, Table 2). SinceV_max is normalized to total protein concentration it was unaffected for both compounds A and B (Fig. 2, Table 2). In addition, correction of K_m,appfor free fraction yielded estimates that appeared to be independent of microsomal concentration for both compounds.

• Download figure
• Open in new tab
• Download powerpoint

Figure 1

Saturation plot for compound A at two different microsomal protein (0.46 and 2.3 mg/ml) and enzyme (0.25 and 1.0 μM CYP) concentrations.

Solid lines represent the best fit to the data from individual runs using the Michaelis-Menten equation. The dashed line represents a simulation using the estimated parameters, following correction for nonspecific microsomal binding. Error bars represent standard deviation.

• Download figure
• Open in new tab
• Download powerpoint

Figure 2

Saturation plot for compound B at two different microsomal protein (0.46 and 2.3 mg/ml) and enzyme (0.25 and 1.0 μM CYP) concentrations.

Solid lines represent the best fit to the data from individual runs using the Michaelis-Menten equation. The dashed line represents a simulation using the estimated parameters, following correction for nonspecific microsomal binding. Error bars represent standard deviation.

Discussion

Hepatic microsomal lability represents one of the simplest and most widely used tools to predict human clearance during the drug discovery process (Iwatsubo et al., 1997; Rodrigues, 1997; Obach, 1999). Two methods are commonly employed, including thet_1/2 method, in which the first order rate of metabolism is determined at low substrate concentrations, and the enzyme kinetic method, in which V_max andK_m are determined (Rane et al., 1977; Obach et al., 1997). Estimates of in vivo intrinsic clearance are typically made through the use of scaling factors applied to the observed in vitro data on the basis of protein concentration (Houston, 1994). As previously reviewed, this use of microsomes requires many assumptions, including one that the substrate is freely available for metabolism (Houston and Carlile, 1997). Many compounds can bind nonspecifically to microsomes, thereby invalidating this assumption (Obach, 1996, 1997,1999; Obach et al., 1997; Venkatakrishnan et al., 2000). In these cases, increasing concentrations of nonspecific binding components within the incubation will decrease the apparent intrinsic clearance of compounds that bind to liver microsomes (Gillette, 1963; Obach, 1997;McLure et al., 2000). Despite the clear implications of these findings for scaling intrinsic clearance, methods disregarding all protein binding considerations can yield clearance projections of the same accuracy as those that account for the extent of plasma and microsomal binding (Obach, 1999). Discussion of this phenomenon in the literature frequently follows a delineation of the impact of binding corrections and experimental outcomes around physiochemical properties (Obach, 1999; McLure et al., 2000). Although the conclusions of these analyses may have empiric value, they do not directly relate the underlying factors known to influence free fraction to the experimental outcomes in a quantitative manner. As such, relationships between the necessity of nonspecific binding considerations and physiochemical properties should be tenuously considered when conducting studies to characterize additional compounds. Herein, we have theoretically and experimentally illustrated the expected impact of microsomal concentration on several parameters that are commonly reported as measures of microsomal lability. Projected and observed results were quantitatively compared in terms of -fold changes to fu_mic,t_1/2, CL_int,app, andK_m,app. The theories were derived from very simple rearrangements of the relationship between free fraction and binding component concentration (Romer and Bickel, 1979). Two proprietary compounds were chosen to experimentally illustrate two extremes depicted by the derived theories, viz.; high nonspecific binding and low nonspecific binding. The highly bound representative (compound A, fu_mic = 0.055) was a basic and highly lipophilic compound, whereas the compound representative of low binding (compound B, fu_mic = 0.86) was a slightly less lipophilic acid (Table 1). Although the structures of these compounds are not revealed, we submit that the conclusions have general applicability to other compounds regardless of specific chemical structures or physiochemical characteristics.

High Nonspecific Binding.

A 5-fold increase in microsomal concentration was associated with a proportional decrease in the free fraction of compound A (Table 2). No difference in metabolic half-life was observed; however, scaling of the observed microsomal t_1/2 to an estimate of apparent intrinsic clearance resulted in a 5-fold lower value at the higher microsomal concentration (Table 2). Consistent with this result, the K_m,app of compound A increased proportionally to the increase in microsomal concentration (Table 2, Fig. 1). Each of these observations is consistent with the expected behavior for a highly bound compound predicted by eqs. 2, 7, and 9. We conclude that the 5-fold difference in CYP concentration is offset by an inversely proportional change in free fraction. This conclusion was supported when correction for the free fraction available for metabolism resulted in virtually identical estimates of intrinsic clearance under both conditions (Table 2). Although these findings are in general agreement with recent simulations published by McLure et al. (2000), the lack of a direct quantitative relationship between these variables in that study prevents a detailed comparison. We expect that this class of compounds will frequently require the correction factor previously proposed by Obach (1996) for free fraction differences between plasma and microsomes to accurately predict clearance in vivo. In this circumstance, the quantitative differences in protein and lipid content between microsomes and plasma alone could reasonably be expected to result in significant differences in the free fraction between these two matrices. Since the free fraction in microsomes is determined, in part, by the choice of microsomal concentration in the incubation, equivalent free fractions between plasma and microsomes should be considered coincidental. It is therefore unlikely that the clearance of these compounds will be accurately predicted by disregarding all binding. These data also suggest that one could avoid indiscriminate and labor intensive protein binding studies by determining the metabolic half-life at two different microsomal concentrations. If half-life is unchanged, then the compound may be highly bound. If half-life is changed proportionally then the compound is expected to have a low extent of nonspecific binding as described below.

Low Nonspecific Binding.

Less than proportional changes in the free fraction of compound B were observed relative to microsomal concentration (Table 2). It is important to note that a nonlinear decrease in free fraction was observed at the higher microsomal concentration. This is consistent with eq. 1, which predicts that compounds with high free fractions will be influenced nonlinearly by changes in the concentrations of nonspecific binding components. At 5-fold higher microsomal concentration, the t_1/2 of compound B was decreased by greater than 3-fold (Table 2). The slight difference in free fraction, observed in this case, contributes to the slightly less than proportional difference in t_1/2 (Table2). Scaling of the observed microsomal t_1/2to CL_int,app, resulted in estimates that were relatively independent of microsomal concentration (Table 2). Consistent with this result, the K_m,app of compound B was also relatively independent of microsomal concentration (Table 2, Fig. 2). Again, the slight difference in free fraction may account for the small differences in CL_int,appand K_m,app. This is evidenced by the even smaller differences in these parameters when corrected for free fraction (Table 2). Each of these observations is consistent with the expected behavior predicted by eqs. 2, 7, and 9 for a compound with low nonspecific binding. In this case, we conclude that the increase in CYP afforded by increasing the microsomal concentration within the incubation is accomplished without a significant effect on the free fraction of substrate available for metabolism. Becauset_1/2 from the microsomes decreases proportionally, scaling of intrinsic clearance results in estimates that are independent of microsome concentration. We expect that this class of compounds may not require the correction factor previously proposed by Obach (1996) for free fraction differences between plasma and microsomes to accurately predict clearance in vivo. However, it is important to note that highly free compounds in microsomes may still be highly bound to plasma proteins. In such cases, it may be possible to ignore in vitro microsomal protein binding but necessary to account for plasma protein binding when predicting clearance.

In summary, we have derived a series of companion equations that quantitatively illustrate the combined influences of nonspecific binding component and enzyme concentration on several relevant kinetic endpoints in a manner that is intuitively understood. Two compounds were chosen to experimentally illustrate the expected results under two distinct situations, namely a high and low degree of nonspecific microsomal binding. These results illustrate that, regardless of physiochemical properties themselves, compounds with a high degree of nonspecific binding to microsomes are likely to require additional considerations for free fraction when predicting clearance in vivo. We believe this work offers additional theoretical and practical clarity to the appropriate design and interpretation of microsomal lability assays.