Abstract
A data-driven approach was adopted to derive new one- and two-species-based methods for predicting human drug clearance (CL) using CL data from rat, dog, or monkey (n = 102). The new one-species methods were developed as CLhuman/kg = 0.152 · CLrat/kg, CLhuman/kg = 0.410 · CLdog/kg, and CLhuman/kg = 0.407 · CLmonkey/kg, referred to as the rat, dog, and monkey methods, respectively. The coefficient of the monkey method (0.407) was similar to that of the monkey liver blood flow (LBF) method (0.467), whereas the coefficients of the rat method (0.152) and dog method (0.410) were considerably different from those of the LBF methods (rat, 0.247; dog, 0.700). The new rat and dog methods appeared to perform better than the corresponding LBF methods, whereas the monkey method and the monkey LBF method showed improved predictability compared with the rat and dog one-species-based methods and the allometrically based “rule of exponents” (ROE). The new two-species methods were developed as CLhuman = arat-dog · W human0.628 (referred to as rat-dog method) and CLhuman = arat-monkey · W human0.650 (referred to as rat-monkey method), where arat-dog and arat-monkey are the coefficients obtained allometrically from the corresponding two species. The predictive performance of the two-species methods was comparable with that of the three-species-based ROE. Twenty-six Wyeth compounds having data from mouse, rat, dog, monkey, and human were used to test these methods. The results showed that the rat, dog, monkey, rat-dog, and rat-monkey methods provided improved predictions for the majority of the compounds compared with those for the ROE, suggesting that the use of three or more species in an allometrically based approach may not be necessary for the prediction of human exposure.
Allometric scaling has been one of the most widely used approaches for predicting human drug clearance (CL) based upon measured values of CL in animal species (Boxenbaum, 1982). Because of its empirical nature and the numerous observed failures in predicting human CL, various modified allometrically based scaling methods have been proposed with the intent of improving predictability in humans. These methods primarily include corrections for maximum life-span potential (MLP) (Boxenbaum, 1982), corrections for brain weight (BrW) (Mahmood and Balian, 1996b), corrections for un-bound fraction of drug in plasma (fu) (Feng et al., 2000), the “rule of exponents” (ROE) (Mahmood and Balian, 1996a), liver blood flow (LBF) methods (Nagilla and Ward, 2004), corrections for in vitro metabolic CL (Lave et al., 1996), and empirical models correcting for plasma binding differences between animals and humans (Tang and Mayersohn, 2005c). The ROE technique has gained considerable support because of the soundness and practicality of the approach in correcting for MLP or BrW in each animal species; these correction procedures lower the prediction of human CL when a relatively high exponent is obtained from simple allometry (SA). Recently, Ward and Smith (2004) challenged the ROE approach after analyzing 103 sets of allometric data from the rat, monkey, and dog. They concluded that the ROE method provided no significant improvement for human predictions of CL compared with SA. Furthermore, they recommended that the monkey LBF method be used for the most accurate and reliable estimation of human clearance based on the results they obtained with various methods including three-species allometry. The controversy concerning which animal species to use, which criteria to use for assessing prediction performance, and issues of data quality, has been discussed recently in a commentary by Mahmood (2005a) and correspondence by Nagilla and Ward (2005).
More recently, a general allometric equation (GAE), which provides predictions based on log-log transformation followed by linear regression of the allometric power function, has been derived to illustrate the role of species selection in allometric scaling. The GAE demonstrated that the predictions in humans are highly species-dependent. Most interestingly, the GAE revealed that some species made little or no contribution to the predicted value in humans when a combination of animal species is used in allometric scaling. For example, the rat contributes little to the predicted value in humans as long as the rat is not the species having the lowest body weight in a combination of three or more species (Tang and Mayersohn, 2005a). In addition, the functionality of applying correction factors in allometric scaling was found to be equivalent to applying certain constant values that are predetermined on the basis of the species used and bear no relationship to values of CL in the animals (Tang and Mayersohn, 2005b). Tang and Mayersohn (2006) further proposed fixing exponents in allometry as an alternative to the ROE. In summary, there is some evidence to suggest that using three or more animal species in an allometrically based prediction may not be necessary.
In this report, using the published intravenous CL data sets (n = 102) in rat, dog, monkey, and human (Jolivette and Ward, 2005), we derived, based on a data-driven approach, new one-species methods for predicting human CL and compared them to the LBF methods and the allometrically based ROE. In addition, allometrically based two-species methods with fixed exponents, which were optimized from the above data sets, were derived and compared with the allometrically based ROE. These methods were further tested using compounds (n = 26) developed at Wyeth.
Materials and Methods
Model Development and Internal Validation. Intravenous CL data for the rat, dog, monkey, and human used for the development of the LBF methods (Jolivette and Ward, 2005) were used in developing the new methods proposed here. This data set, to the authors' knowledge, is the largest data set published for commercial drugs, which are pharmacokinetically diverse. For the model building, data for iododoxorubicin from the original data set were not used because it was an obvious outlier. The LBF method is described as 
where coefficientLBF = (LBFhuman/LBFanimal).
Similar to the LBF method, the one-species method proposed here is based on the following relationship: 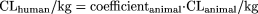
The coefficientanimal was obtained by minimizing the objective function of average absolute fold-error (AAFE) and by optimizing the objective function of AFE (average fold-error) at 1, where 

and 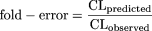
AAFE (Obach et al., 1997) and AFE are measures of precision and accuracy of the overall prediction, respectively, and N represents the total number of compounds. Note that AFE, which does not take the absolute values of sum of log(fold-error), is the geometric mean of fold-errors and allows measurement of the overall bias (difference from the reference value at 1) in both directions; less than or greater than 1 indicates an overall under- or overprediction, respectively. The prediction performance was also assessed using the percentage of outliers falling out of the preselected fold-error ranges of [0.5-2.0] or [0.33-3.0].
The same set of data was used to develop the two-species methods using a combination of rat and dog or rat and monkey described as 
where atwo-species is the coefficient obtained from conventional allometric scaling of the two-species data and bfixed is a fixed value that was obtained by minimizing the objective function of AAFE and optimizing the objective function of AFE at 1.
The optimizations were carried out with S-PLUS (version 6.1; Insightful Corporation, Seattle, WA) with tolerance set at 0.00001. The nonparametric bootstrap approach was applied for the internal validation of the one- and two-species models. Five hundred resamplings were performed and the resulting distributions, mean, bias, and standard error of the coefficients (for the one-species methods) and exponents (for the two-species methods) were computed.
Testing New Methods with Wyeth Compounds. Animal and human data for 26 Wyeth compounds were used to test the new methods. Among the 26 compounds having both i.v. and p.o. data, 26 were in mice (CL ranged from approximately 3.03 to 242 ml/min/kg), 26 were in rats (CL ranged from approximately 3.19 to 299 ml/min/kg), 21 were in dogs (CL ranged from approximately 0.405 to 116 ml/min/kg), and 9 were in monkeys (CL ranged from approximately 3.63 to 32.7 ml/min/kg), whereas in humans, only 6 compounds had i.v. data as the majority of the compounds were developed for oral administration. For the compounds that were intended for oral administration, the human clearance was predicted from the clearance in animals after i.v. administration. The predicted human exposure based on i.v. clearance was then corrected for the anticipated human bioavailability to obtain the predicted oral exposure after oral administration. Therefore, the prediction performance was assessed using the fold-errors of i.v. or p.o. exposure [area under the concentration-time curve (AUC)] between predicted and observed values. The prediction of bioavailability (F) in humans was based on the average of F in two animal species for both the one- and two-species methods, as we speculate from a prospective point of view that oral bioavailability data will be available in two animal species (rat and dog or rat and monkey). The average of F in all species (three or more) was used as the predicted F in humans for the SA and ROE methods. The predicted F and the predicted systemic CL in humans were used to predict the p.o. AUC in humans. It is noted that for compounds administered orally, the results of this analysis contain combined prediction errors for CL and bioavailability.
The calculated molar refractivity and the calculated log(octanol/water partition coefficients) (ClogP) were obtained using the cmr and clogp utilities from Daylight Chemical Information Systems (Aliso Viejo, CA). The hydrogen bond donor, hydrogen bond acceptor, and rotational bonds were obtained using internally developed code. Polar surface area was calculated by the method of Ertl et al. (2000).
Rule of Exponents. The ROE was applied as described by Mahmood and Balian (1996a): 1) if the exponent from SA is between 0.55 and 0.70, SA is applied; 2) if the exponent is between 0.70 and 1.0, the CL · MLP correction approach is applied; 3) if the exponent is greater than 1.0, the CL · BrW correction approach is applied; or 4) if the exponent is less than 0.50, SA is applied because none of the approaches could improve the prediction. Mahmood (2006) further indicated that the ROE does not apply to compounds which are eliminated via biliary excretion and that the ROE could not correct the large prediction errors for compounds with allometric exponents greater than 1.3. Because no correction method has been proposed for SA with exponents greater than 1.3, the CL·BrW correction approach was used for cases with exponents greater than 1.3, as the CL·BrW correction yields a greater downward correction than the CL·MLP correction (Tang and Mayersohn, 2005b). During drug development (phase 0), the information on whether a compound undergoes predominantly biliary excretion in animals or humans may not be available until the compound is in late development; therefore, no subsequent correction factors such as those described by Mahmood (2005b) for biliary excretion drugs were applied as the analysis was carried out as a prospective approach.
Results
The coefficients/exponents based on minimization of AAFE were 0.161, 0.429, 0.466, 0.633, and 0.650 for the rat, dog, monkey, rat-dog, and rat-monkey methods, respectively. The corresponding coefficients/exponents based on the optimization of AFE at 1 were 0.152, 0.410, 0.407, 0.628, and 0.650, respectively. Because these two sets of values were close, only optimized coefficients or exponents based on the optimization of AFE of 1, which have been successfully achieved for all the models, are reported. The new one- or two-species methods with optimized coefficients or exponents are as follows: 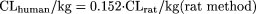



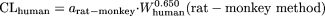
The bootstrap coefficients for the one-species methods and exponents for the two-species methods were symmetrically distributed around the observed values (data not shown). The bootstrap means (relative standard errors, defined by the standard errors divided by the means) for the coefficients of the rat, dog, and monkey methods and the exponents of the rat-dog and rat-monkey methods were 0.153 (11.0%), 0.412 (13.6%), 0.409 (9.5%), 0.650 (3.2%), and 0.628 (4.3%), respectively. The facts that the bootstrap means are very close to the corresponding observed values (0.152, 0.410, 0.407, 0.650, and 0.628, respectively) and the relative standard errors are small indicate that these are robust models. The value for the coefficient of the monkey method (0.407) is close to that of the monkey LBF method (0.467). However, the values for the coefficients of the rat and dog methods are approximately 1.6-fold lower than those of the corresponding LBF methods (Table 1), indicating that the predictions of CL in humans based on the rat or dog method are approximately 1.6-fold lower than those based on the LBF methods. The exponents for the rat-dog method and rat-monkey method were 0.628 and 0.650, respectively.
The predictability of various methods for the literature data (training data for the development of new methods, n = 102)
The AFE values for the rat and dog LBF methods were 1.63 and 1.71, respectively, indicating that the rat and dog LBF methods tend to overpredict CL in humans compared with the rat method and dog method (which have optimized AFE values at 1). The values of AAFE for the rat and dog methods were lower than those of the corresponding LBF methods. For both the new and LBF one-species methods using rat or dog, the percentages of outliers falling out of the fold-error ranges of 0.5 to 2 and 0.33 to 3 were approximately 50 and 30%, respectively, with the outlier percentages being slightly higher for the LBF methods. The AFE and AAFE values for the monkey method and monkey LBF method were similar because of the similar coefficients of the two types of methods. In comparison with the rat or dog one-species methods, both the monkey method and the monkey LBF method substantially improved the prediction performance; the AAFE values decreased to approximately 1.9, and the percentages of outliers falling outside the fold-error ranges of 0.5 to 2 and 0.33 to 3 decreased to approximately 30 and 20%, respectively.
The AFE value for the allometrically based ROE was 0.89, indicating that this method tended to slightly underpredict CL in humans compared with the new methods (which have optimized AFE values at 1). The value of AAFE for the ROE was lower than that for the rat and dog methods (suggesting better performance by the ROE), similar to that for the rat-dog method but higher than that for the new rat-monkey and monkey methods (suggesting better performance by the new one- and two-species methods that include monkey). The percentages of outliers falling outside of the fold-error range of 0.5 to 2 were similar for the ROE, the rat and dog one-species methods, and the rat-dog and rat-monkey two-species methods (range 43-50%) but clearly lower for the monkey one-species method (29%). The percentages of outliers falling outside of the fold-error range of 0.33 to 3 were similar for the rat and dog one-species methods and the rat-dog two-species method (range 24-28%) but lower for the ROE, the rat-monkey two-species method, and the monkey one-species method (range 16-20%). Collectively, the data suggest that the monkey LBF method and the new monkey method provide the best overall prediction performance.
The molecular properties (median, range) of the Wyeth compounds versus training sets are, respectively, calculated molar refractivity (10.5, 6-22.4) versus (9, 2.5-23.9); ClogP (4, -2.3 to 10.7) versus (0.9, -7.21 to 5.82); hydrogen bond donor (2, 0-7) versus (2, 0-12); hydrogen bond acceptor (6, 2-15) versus (6, 1-18); polar surface area (88, 15.2-258.8) versus (91.7, 3.2-319.6); number of rotational bonds (6, 0-16) versus (5, 0-16). In general, the distributions of the computational molecular properties of the Wyeth compounds and the training data set are similar except for ClogP, which appeared to have a distribution towards higher values for the Wyeth compounds compared to the compounds in the training data sets. The occurrence of higher ClogP values for Wyeth compounds than those for the compounds in the training data sets (most are marketed drugs) is not unusual, as the current high-throughput technologies tended to produce more lipophilic drug candidates. Although certain observations have been made by Jolivette and Ward (2005) on the associations between the molecular properties and the prediction performance, particularly for ClogP values at 0 and 1 for the rat and dog LBF methods, respectively, the existence of ClogP as a significant covariate for the one-species-based model was lacking. Additionally there were no correlations between the ClogP values and the prediction fold-errors of any one-species-based methods for the training data sets (data not shown). Therefore, the apparent difference in the distributions of ClogP values between the training and test data sets was considered to have no major effect on the application for testing the new one-species methods with the Wyeth compounds.
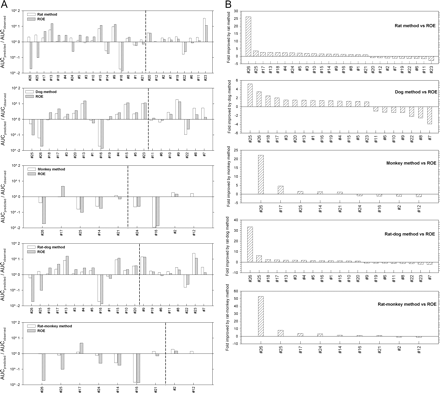
The prediction fold-errors (AUCpredicted/AUCobserved) for the Wyeth test compounds are shown in Table 2. Predictions for the 6 i.v. compounds were within a 3-fold error for all the methods, with the new one- or two-species methods generally having slightly lower prediction fold-errors than the ROE. The comparisons of predictability between ROE and each new method are shown in Fig. 1, A and B. The rat, dog, monkey, rat-dog, and rat-monkey methods provided improved predictions relative to the ROE for 17 of 26, 14 of 21, 5 of 9, 14 of 21, and 7 of 9 compounds, respectively. These data suggest that comparable or improved predictability can be achieved with the new methods using fewer species than required by the ROE. In addition, the new methods showed considerable improvement in the predictions for a few compounds; for example, the AUC prediction in humans for Wyeth compound #26 based on rat, monkey, rat-dog, or rat-monkey methods was considerably improved (∼20-fold) compared with that based on ROE. Indeed, Mahmood (2006) has indicated that the ROE could not correct the large prediction errors for such examples (exponent >1.3) and suggested that other approaches are needed. It appears that the new methods can be applied with adequate results.
Comparisons of the prediction fold-error by SA, ROE, and the new methods for Wyeth compounds (test data, n = 26)
Discussion
Prediction of Oral Exposure. The proposed new methods for examining species scaling reported here were developed using i.v. CL data in each species, whereas most of the data from the Wyeth test compounds were based on oral dosing in humans. We have attempted to examine the new models based on the i.v. data and then use those models to test the Wyeth compounds, regardless of route of administration. Although the ROE and LBF methods have historically been developed and evaluated in terms of predicting human CL, in practice most pharmaceutical products are developed for oral delivery, and, hence, from a drug development perspective these methods are most useful when applied in combination with a prediction of bioavailability to predict human exposure (AUC). It is recognized that when one is dealing with the compounds still in early development, it is not feasible to obtain the bioavailability in humans and, as a result, that parameter was considered a covariate in comparing the performance of the methods (oral exposure) for the Wyeth compounds. However, for the purpose of comparing the new methods against the ROE or SA, F would not have a significant effect on the interpretation of the performance of the methods as long as the estimates of F for the new methods and ROE/SA are comparable. As shown in Fig. 2, the F estimates for the new methods based on two species (rat and dog or rat and monkey) were similar to those for the ROE and SA based on all animal species (mouse, rat, dog, or monkey). Using the F estimates based on all animal species for the new methods generally did not improve the predictions in humans compared with using the F estimates based on two species (data not shown).
Rationale for the Development of One-Species Methods. The idea behind the development of the new one-species methods was that because the LBF methods are empirical in nature, an optimized (or data-driven) empirical method might be more predictive than the LBF-based empirical method. The optimized coefficient for the rat or dog methods was approximately 1.6-fold lower than that of the corresponding LBF methods. It is noteworthy that the coefficient obtained for the rat method agreed with that for the previously reported one-species allometric scaling method with the mean exponent of 0.66 based on 54 extensively metabolized drugs (Chiou et al., 1998); the rat method, CLhuman/kg = 0.152 · CLrat/kg, is very similar to 
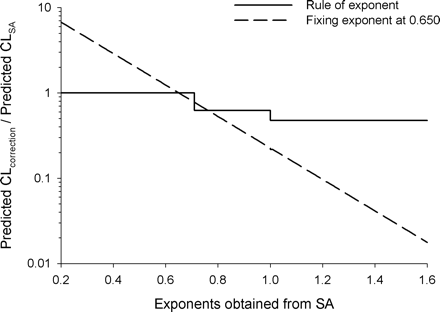
Advantages of Fixing the Exponent in the Two-Species Methods. The ROE has been shown to improve the predictions in humans compared with SA in this work as well as that of others (Mahmood and Balian, 1996a; Tang and Mayersohn, 2005c). This improvement is considered to be the result of downward adjustments of CL predictions in humans based on SA by the MLP or BrW correction. However, the ROE has been shown to function as a set of constants that are predetermined based on species used and that bear no relationship to the values of CL in animals. The magnitude of correction by MLP and BrW varied, approximately 0.326 to 0.622 and 0.172 to 0.474, respectively, for the common combinations of species (Tang and Mayersohn, 2005b). The investigators further proposed that, unlike the stepwise corrections based on the ROE, fixing the exponent would result in a correction magnitude that increases (or decreases) continuously with the exponent value obtained from SA and may provide improved predictability in humans (Tang and Mayersohn, 2006). Figure 3 shows the magnitude of correction using the ROE and a fixed exponent of 0.650 for the combination of species, mouse, rat and monkey. The correction magnitude from fixing the exponent at 0.650 is given by 70(0.65-b), where b is the exponent from SA. In contrast, the correction magnitude from the ROE is a stepwise function (1.0 when b < 0.70, 0.622 when 0.70 < b < 1.0, and 0.474 when b > 1.0). From this analysis, what is of concern is that for the ROE the correction magnitude is bounded at 0.474 no matter how questionable the values of the exponents obtained are. For example, the exponent for Wyeth compound 26 was 1.589, resulting in a prediction fold-error of 0.018 based on the ROE, whereas fixing the exponent at 0.650 resulted in a prediction fold-error close to 1. It is noted that Mahmood (2006) has suggested that the ROE could not correct the large prediction errors for cases in which the exponent is >1.3, whereas it seems, based on the two examples in the Wyeth data set, that the new methods can be applied in these circum-
stances with some success. Additional testing in this area is clearly warranted.
A, pair-wised comparisons of prediction fold-errors (AUCpredicted/AUCobserved) between each of the new methods and the ROE for the Wyeth test compounds. Note that to the left or right of the dashed vertical line are compounds whose predicted AUCs in humans were predicted better by the new methods or the ROE, respectively. B, fold improvement by the new methods compared with the ROE, defined as 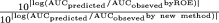 when the new methods provided better predictions, and
when the new methods provided better predictions, and 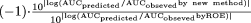 when the new methods provided worse predictions. For example, for compound 26, because the prediction fold-error by the rat method and the ROE were 2.070 and 0.018, respectively, the fold improvement by the rat method was 26.8. Positive or negative values indicate that the predictions were improved or worsened, respectively, by the new methods compared with ROE.
when the new methods provided worse predictions. For example, for compound 26, because the prediction fold-error by the rat method and the ROE were 2.070 and 0.018, respectively, the fold improvement by the rat method was 26.8. Positive or negative values indicate that the predictions were improved or worsened, respectively, by the new methods compared with ROE.
Comparisons of predicted oral bioavailability in humans (Fhuman) based on the average bioavailability of two animal species (A, rat and dog; B, rat and monkey) and all animal species (at least with the addition of the mouse). The solid line is the line of identity.
Comparisons of correction magnitudes by ROE and that from fixing the exponent at 0.650 for the combination of mouse, rat, and monkey.
In addition, by theory, the variability of predicted values in humans using the model  (fixed-exponent model) is less severe compared with extrapolating the power function
(fixed-exponent model) is less severe compared with extrapolating the power function 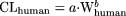 (allometric model), where b is a variable. The predicted value in humans using the former model is also less dependent on any one species compared with extrapolating the latter model. These two points can be illustrated in the following example. The general allometric equation (Tang and Mayersohn, 2005a) is described as
(allometric model), where b is a variable. The predicted value in humans using the former model is also less dependent on any one species compared with extrapolating the latter model. These two points can be illustrated in the following example. The general allometric equation (Tang and Mayersohn, 2005a) is described as 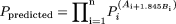
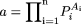
where n different animal species are used in allometric scaling, Pi is the value of the pharmacokinetic parameter in the ith animal species, 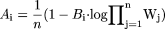
and 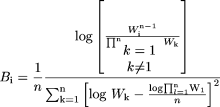
where W is the body weight of a specified animal species.
Using the typical body weight of mouse (0.03 kg), rat (0.3 kg), monkey (5 kg), and human (70 kg), then 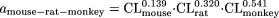
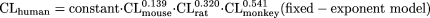
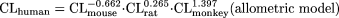
It is obvious that the variability of the fixed-exponent model is less than that associated with the allometric model, because the range of the exponents [0.139 to 0.541] of CL for each species in the fixed-exponent model is much narrower than that [-0.662 to 1.397] for the allometric model. In addition, the differences in the absolute values of the exponents in the fixed-exponent model are much smaller than those in the allometric model; thus, the CL predicted in humans is less dependent on any one species (for example, monkey CL in this example is the major determinant of predicted human CL for this combination of species).
The Coefficient,a, Obtained from a Combination of Two Species Is Comparable to That from Three Species. The coefficient, a, obtained from the combination of two species should, by theory, be close to that obtained from the combination of three species; this is the reason that the coefficient obtained from two species can be used in the new proposed two-species method. For example, based on the general allometric equation given above, the coefficient obtained from rat and monkey is given by 
Together with the previous expression for amouse-rat-monkey, 
Because the body weight between mouse and rat or between rat and monkey differs by more than 10-fold, it is safe to assume that for the majority of compounds, the total body CL will follow the order, CLmonkey > CLrat > CLmouse. It is also reasonable to assume that for the majority of compounds, CLmonkey < 1000 · CLrat and CLrat < 1000 · CLmouse, given only approximately a 10-fold difference in body weights. Then 
Therefore, the coefficient obtained using rat and monkey will not be much different from that obtained using mouse, rat, and monkey. Even in some extreme situations, for example, when CLmonkey = CLrat = 1000 · CLmouse (note: Wmonkey ≅ 17 · Wrat ≅ 170 · Wmouse), the resulting ratio, amouse-rat-monkey/arat-monkey, is only approximately 0.382. For the vast majority of situations, the values of amouse-rat-monkey/arat-monkey should be very close to 1. The comparable values of the observed coefficients based on two species (rat and dog or rat and monkey) and three species (mouse, rat, and dog or mouse, rat, and monkey) for the Wyeth compounds agreed with the above theory (Fig. 4).
Comparisons of the coefficients obtained based on two species (A, rat and dog; B, rat and monkey) and three species (with the addition of the mouse) for the Wyeth compounds. The solid line is the line of identity.
It should be noted that the one- or two-species-based methods do not invalidate the principle of allometry (Boxenbaum, 1982); in fact, they conform with the principle of allometry. The allometric relationships of various physiological relationships (metabolic rate, tissue weight, blood flow rate, blood volume, etc.) have been well established with data from many species (Mordenti, 1986). However, the existence of an allometric relationship for a physiological parameter does not mean that a similar allometric relationship can be established with a limited number of species. The allometric exponent of 0.67 (⅔ power law) or 0.75 (¾ power law) for the metabolic rate has been established with hundreds of species (White and Seymour, 2005); using a limited number of species, for example, three species, may result in an allometric relationship of metabolic rate that is very different from that obtained from hundreds of species. The same logic can be applied to the application of allometric scaling for predicting human CL: using a limited number of animal species may result in an allometric relationship that has an exponent deviating from approximately 0.6 to 0.9 and extrapolation based on such a relationship to humans over a wide range of body weights may be risky. Thus, allometric relationships of CL having exponents deviating considerably from 0.6 to 0.9 while providing successful predictions in humans are rare. This observation is also consistent with those of Mahmood and Balian (1996b) that the ROE, which lowers the predictions by SA when a relatively high exponent is obtained, can improve the predictions over SA. Therefore, fixing the coefficients (one-species methods) or the exponents (two-species methods) that had reasonable values around approximately 0.6 to 0.7 actually abides by the principle of allometry.
In summary, this work presents the logic of how the allometrically based approach using CL data from three or more species can be reduced to an approach that uses one or two species for predicting human CL and derives new methods for predicting human CL (using one or two animal species) based on a data-driven approach. The new one-species methods generally agree with the empirical one-species LBF methods, particularly the monkey method. The coefficients of the rat and dog methods differ approximately 1.6-fold from those of the corresponding LBF methods and appeared to have better predictability than the corresponding LBF methods. This finding, however, should be subjected to further testing. The new two-species methods with the optimized exponents can be considered as variants of the allometrically based ROE using three or more species. Fixing the exponents in the new two-species methods provides continuous corrections (either up or downward), contrasting with fixed stepwise downward corrections with the ROE. Furthermore, the latter method provides no solution to correct for exponents smaller than 0.55 or greater than 1.3. Based on the training data sets, both the new monkey method and the monkey LBF method were shown to provide improved predictability compared with the other methods, including the rat or dog one-species-based methods and the ROE. On the basis of the Wyeth compounds used in this analysis, the presence of the mouse data did not provide any advantage, and thus the mouse is considered to be an unnecessary species, as the new one- or two-species approaches generally appeared to be as predictive as or more predictive than the ROE or SA, which used three species, including the mouse.
It should be noted that the application and choice of the new methods will depend on the available data and the exceptional characteristics of a compound being investigated. The real circumstances that are needed to be dealt with are often more complicated than just using an equation; for example, the in vitro metabolism data, plasma protein binding, and prediction of bioavailability, are always important factors that need to be considered to optimize the predictions. A further analysis of the prediction outliers of the Wyeth compounds with regard to the effect of these factors on the predictions will be detailed in another report.
Footnotes
-
doi:10.1124/dmd.107.016188.
-
ABBREVIATIONS: CL, clearance; MLP, maximum life-span potential; BrW, brain weight; ROE, “rule of exponent”; LBF, liver blood flow; SA, simple allometry; GAE, general allometric equation; AAFE, absolute average-fold error; AFE, average-fold error; AUC, area under the concentration-time curve; ClogP, calculated log(octanol/water partition coefficient); F, bioavailability.
- Received April 10, 2007.
- Accepted July 19, 2007.
- The American Society for Pharmacology and Experimental Therapeutics