The use of in vitro data to predict in vivo clearance or assess drug-drug interaction potential is well established (Bjornsson et al., 2003; Ito and Houston, 2005; Galetin et al., 2006; Huang et al., 2007; Rostami-Hodjegan and Tucker, 2007). Binding to microsomal protein and phospholipids has been recognized as an important parameter in the in vitro-in vivo extrapolation strategies (Obach, 1999; McLure et al., 2000; Tucker et al., 2001; Margolis and Obach, 2003; Galetin et al., 2005; Ito and Houston, 2005; Brown et al., 2006). Nonspecific binding to microsomes may lead to underestimation of in vivo clearance (Obach, 1996, 1999; Ito and Houston, 2005; Grime and Riley, 2006) or can result in significantly higher IC₅₀ or K_i values in the assessment of inhibition interaction potential (Margolis and Obach, 2003; Brown et al., 2006). Although generally accepted to improve the accuracy of in vitro-in vivo predictions (in conjunction with other in vitro parameters), the assessment of microsomal binding in the form of fu_inc is still challenging.

One way to avoid the complications of nonspecific binding is to use very low microsomal concentrations, a common practice in high-throughput screening, in particular with recombinant enzymes showing high enzyme activity (Obach et al., 2006). This is also consistent with recommendations that depletion incubations should be carried out at microsomal protein concentrations below 0.5 mg/ml (Jones and Houston, 2004). However, higher microsomal protein concentrations are required under certain conditions, such as when studying phase II metabolic reactions (Soars et al., 2002; Mohutsky et al., 2006) or intestinal metabolism (Galetin and Houston, 2006). In addition, most of the in vitro assessment of the time-dependent inhibition potential is based on the use of high protein concentrations (1–2 mg/ml) in order to allow adequate dilution in the two-step experimental procedure (Ghanbari et al., 2006). It should also be noted that highly lipophilic drugs might show significant nonspecific binding even at low microsomal protein concentration.

Recently, two algorithms have been introduced by Austin et al. (2002) and Hallifax and Houston (2006) for the prediction of fu_inc. Both predictive tools are based on the lipophilicity of the compounds investigated, as defined by either logD_7.4 (for acidic and neutral compounds) or logP for bases and the microsomal protein concentration (see Materials and Methods). Austin et al. (2002) compiled a data set of 41 fu_inc values in rat liver microsomes and 15 fu_inc values in human liver microsomes at a concentration of 1 mg/ml. The data set included compounds from different chemical classes and covered a wide range of logP/D values.

Hallifax and Houston (2006) extended the Austin et al. (2002) data set by incorporating 36 additional drugs. The resulting data set of 92 drugs covered a range of lipophilicity from logP/D =-2.11 to 7.2. The authors proposed that the relationship between logP/D and microsomal binding [log([1 - fu_inc]/fu_inc)] was nonlinear, in contrast to the linear relation defined by Austin et al. (2002). Hallifax and Houston (2006) concluded that the latter empirical equation gave more unbiased predictions of fu_inc for drugs with low binding affinity (fu_inc > 0.9) when compared with Austin et al. (2002).

The aim of this study was to identify limitations within these empirical methods and differences between the respective predictions in order to assess their general applicability. A systematic comparison of predicted and observed fu_inc for a large data set of compounds at different microsomal protein concentrations is currently lacking in the literature. In addition, the source of logP/D (experimental or predicted value) and the impact of its variability on the prediction of fu_inc were also investigated.

The impact of lipophilicity and microsomal protein concentration was assessed using a data set of 127 compounds [35 from our own investigation data and 92 from the data set of Austin et al. (2002) and Hallifax and Houston (2006)]. The fu_inc values were experimentally determined using high-throughput dialysis (Banker et al., 2003) at three protein concentrations (0.1, 0.5, and 1.0 mg/ml). The observed fu_inc values were compared with the values predicted by the Austin and Hallifax equations. The impact of lipophilicity was examined at a 0.1 to 1.0 mg/ml microsomal concentration, covering a representative range of logP/D values from low (<2.5), to medium (2.5–5), to high (>5). The implications of these findings on the prediction of fu_inc, in particular for medium and highly lipophilic compounds, are discussed.

Materials and Methods

Sensitivity Analysis. A simulated fu_inc data set was generated using the Austin and Hallifax equations (eqs. 1 and 2, respectively) over a range of lipophilicity (logP/D = 0–8) and varying microsomal protein concentration (C) from 0.05 to 2 mg/ml. Comparison of the two equations was performed at four distinct areas of lipophilicity, namely logP/D = 0 to 2.5, 2.5 to 5, 5 to 7, and >7, 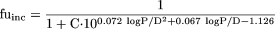where logD_7.4 represents the logarithm of the ratio of the concentration of all drug species (ionized and unionized drugs) distributed between octanol and water at pH = 7.4 (used for acidic and neutral drugs) and logP represents the logarithm of the ratio of the concentration of unionized drug partitioned between octanol and water (used for basic drugs).

Experimental fu_inc Data Set. The fu_inc values were experimentally determined for 35 compounds at microsomal protein concentrations of 0.1, 0.5, and 1.0 mg/ml using the high-throughput dialysis method as described by Banker et al. (2003). All compounds were purchased from Sigma Chemicals Co. (Poole, Dorset, UK), apart from carvedilol, indinavir, ritonavir, and zidovudine, which were obtained from Sequoia Research Products (Pangbourne, West Berkshire, UK). Microsomal binding was determined using pooled human liver microsomes (n = 22) obtained from BD Gentest (Woburn, MA). Dialysis membranes had a 12 to 14 kDa molecular mass cutoff and were purchased from HTDialysis, LLC (Gales Ferry, CT). Phosphate buffer was added to the acceptor chamber with substrate (5 or 10 μM), and microsomes were added to the donor chamber at three protein concentrations (0.1, 0.5, and 1.0 mg/ml). The dialysis plate was left to equilibrate for 20 h on a plate shaker (450 rpm) at 37°C. At the end of the experiment, samples were transferred to a 96-well plate with acetonitrile containing the corresponding internal standard.

Linearity. Peak areas for drugs with relatively low lipophilicity (logP/D < 2.5) were considered to be comparable in the donor and acceptor chamber. Additional in-house calibration data over the appropriate concentration range was available for buspirone, warfarin, mycophenolic acid, codeine, diclofenac, repaglinide, indinavir, and nifedipine. In the range of logP/D 2.5 to 5, linearity data were available for 13 of the 17 drugs investigated; therefore, for the remaining drugs, linearity, when comparing the area of the peaks, was assumed. For the compounds with high lipophilicity, in-house linearity was available for terfenadine, raloxifene, and troglitazone but not for mibefradil, ritonavir, and tamoxifen.

Literature fu_inc Data Set. A data set of fu_inc values for 92 compounds was collated from Austin et al. (2002) and Hallifax and Houston (2006). As the fu_inc values were determined at different microsomal protein concentrations, reported values were standardized to give fu_inc values at 0.1, 0.5, and 1.0 mg/ml using eq. 3, where K_a is the microsomal protein binding affinity.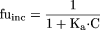

LC-MS/MS. The LC-MS/MS system used consisted of a Waters 2790 with a Micromass Quattro Ultima triple quadruple mass spectrometer (Waters, Milford, MA). Samples were centrifuged at 2500 rpm for 10 min, and an aliquot of 10 μl of both the dialysate and buffer was analyzed by LC-MS/MS. Varying gradients of four mobile phases were used, the compositions of which were 1) 90% water and 0.05% formic acid with 10% acetonitrile, 2) 10% water and 0.05% formic acid with 90% acetonitrile, 3) 90% water and 10 mM ammonium acetate with 10% acetonitrile, and 4) 10% water and 10 mM ammonium acetate with 90% acetonitrile. For all compounds except carvedilol and buspirone, a Luna C18 column (3 μm, 50 × 4.6 mm) was used for chromatographic separation of analytes. For carvedilol and buspirone, a Luna Phenyl-Hexyl column (Phenomenex, Torrance, CA) (5 μm, 30 × 4.6 mm) was used for chromatographic separation of analytes. The flow rate was set at 1 ml/min, and this was split to 0.25 ml/min before entering the mass spectrometer. Further analytical parameters are described in Table 1.

Calculations. The fraction unbound was calculated using eq. 4.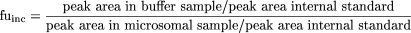

The experimentally determined fu_inc values at microsomal protein concentrations ranging from 0.1 to 1.0 mg/ml for the current data set (n = 35) were compared with the predicted values by both Austin and Hallifax equations. The experimental data set in the current study was expanded by including the fu_inc values for 92 drugs from previous publications (Austin et al., 2002; Hallifax and Houston, 2006), covering a lipophilicity range from -2.1 to 7.2. The bias of experimental fu_inc was assessed from the geometric mean of the ratio of predicted and actual value [average-fold error (afe), eq. 5]. The root mean squared prediction error (rmse) (eq. 6) provided a measure of precision for the predictions of the fu_inc values (Sheiner and Beal, 1981; Obach et al., 1997).

Prediction of LogP Values. Experimental logP data were obtained from the online database ChemIDplus Advanced (http://chem.sis.nlm.nih.gov/chemidplus) for 20 of the investigated 35 drugs. As experimental logP data were not available for all drugs investigated, five online predictive software packages [DrugBank (http://redpoll.pharmacy.ualberta.ca/drugbank), Sparc version 3.1 (http://ibmlc2.chem.uga.edu/sparc/smiles/smiles.cfm), Syracuse Research Corporation (http://www.syrres.com/esc/est_kowdemo.htm), ACD LogP (http://www.emolecules.com/index.php), and Interactive Analysis LogP (http://www.chemsilico.com)] were evaluated for their prediction accuracy. The evaluation was undertaken by comparing experimentally determined logP values for 49 drugs collated from the online database ChemIDplus Advanced to the predictions obtained by the aforementioned software packages. Consequently, the mean of the Syracuse Research Corporation, ACD, and Interactive software packages was used to predict the values for the 15 drugs with unknown logP. The pK_a values for the acids investigated were obtained from the online database ChemIDplus Advanced or from Sparc version 3.1. The logD_7.4 values were then calculated for the acidic drugs using eq. 7:

The impact of variability in logP estimates on the fu_inc predictions by both predictive equations was assessed by propagating a 20% variation in the predictions of logP.

Results

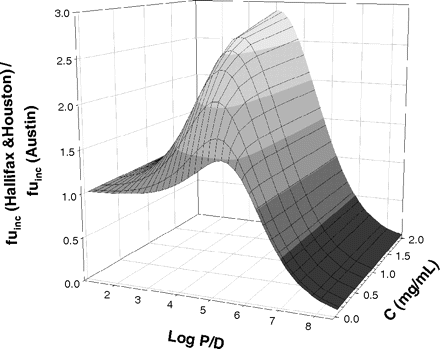
Sensitivity Analysis. A simulated fu_inc data set generated by both Austin and Hallifax equations was compared over a range of microsomal protein concentrations (C = 0.05 - 2 mg/ml). At logP/D ≥ 0, lipophilicity had a greater influence on the fu_inc prediction than the microsomal protein concentration for both equations. This effect was more pronounced for the Hallifax equation. Both equations predicted drugs with very high lipophilicity (logP/D ≥ 7) to be bound >90% to microsomal protein, even at C as low as 0.05 mg/ml (Fig. 1).

Four distinct areas of lipophilicity were investigated: low (logP/D = 0–2.5), intermediate (logP/D = 2.5–5), high (logP/D = 5–7), and very high lipophilicity (logP/D ≥ 7). No major difference between the two equations was observed for the areas of low and high lipophilicity. However, for logP/D values between 2.5 and 5, the Hallifax equation showed up to 3-fold higher predictions in comparison with Austin (Fig. 1). At very high lipophilicity (logP/D ≥ 7), the largest discrepancy between the two equations was observed. Inversely to the situation at medium lipophilicity, predictions of fu_inc by the Austin equation were higher than predictions by the Hallifax equation, and the ratio of the two equations tended toward 0 (Fig. 1). Throughout the range of lipophilicity, minimal difference in the predicted fu_inc values was observed at low microsomal protein concentration.

Prediction of LogP Values. Due to the lack of availability of experimentally determined logP values for 15 of the 35 drugs investigated, a prediction-based approach was used to obtain the unknown logP values. Of the five software packages investigated, Syracuse Research Corporation, ACD, and Interactive showed the highest prediction accuracy and were ultimately chosen. Each of the individual predictive software tools gave logP predictions with low bias and high precision (data not shown). However, the mean of the three selected tools showed the highest prediction accuracy, as indicated by the correlation coefficient (r² = 0.957), bias (afe = 1.07), and precision (rmse = 0.52) (Fig. 2). From the evaluation data set, 78% of the predicted logP estimates were within 20% of the experimental values. Especially good predictions were observed for drugs with logP/D ≥ 2, where 26/29 of the predictions were within 20% and 18/29 of the predictions were within 10% of the experimental values.

Impact of Microsomal Protein Concentration on the Predictions of fu_inc. To investigate the impact of microsomal protein concentration, the fu_inc values of 35 drugs were experimentally determined at three different microsomal protein concentrations—0.1, 0.5, and 1.0 mg/ml. The experimental fu_inc values obtained were compared with the estimates predicted by both Austin and Hallifax equations, as shown in Table 2. In addition to these, fu_inc values for 92 drugs previously published by Austin et al. (2002) and Hallifax and Houston (2006) were included in the analysis, resulting in the data set of 127 compounds. Overall, a decrease in prediction accuracy was observed with increasing microsomal protein concentration (Table 3). This effect was more noticeable for the equation of Austin, whereas the equation of Hallifax resulted in comparable bias in the predictions regardless of the microsomal protein concentration. Particularly high discrepancy between predicted and experimentally obtained values was observed for the fu_inc prediction of felodipine with the Hallifax equation (6-fold over-prediction at C ≥ 0.5 mg/ml). Conversely, the fu_inc value of ritonavir was under-predicted by more than 1000% by both equations.

Low microsomal protein concentration (0.1 mg/ml). Both equations gave highly accurate fu_inc predictions with very low bias. The success of prediction within 1.5-fold was comparable between the equations (81 and 85% for Austin and Hallifax, respectively). In addition, both equations resulted in a similar number of estimates outside 2-fold of the observed value (∼8% for both equations).

Medium microsomal protein concentration (0.5 mg/ml). Use of the Hallifax equation resulted in better predictions at this microsomal protein concentration, whereas the Austin equation on average underpredicted the fu_inc values by 22%. Overall, the extent of predictions found within 1.5-fold decreased, and a higher percentage of predictions was found outside 2-fold for both equations in comparison with 0.1 mg/ml (Table 3).

High microsomal protein concentration (1.0 mg/ml). Accuracy in the predictions further decreased for both equations. On average, the Hallifax equation predicted fu_inc with higher accuracy; 69% of the fu_inc values were within 1.5-fold of the line of unity and 23% outside 2-fold (Table 3).

Impact of Lipophilicity on the Prediction of fu_inc. In addition to microsomal protein concentration, the impact of lipophilicity on the prediction of the fraction unbound was investigated. In the data set of 127 compounds, the lipophilicity ranged from -2.1 (cinoxacin) to 7.2 (amiodarone), providing a representative distribution across the range of lipophilicity of interest.

Low lipophilicity (logP/D < 2.5). Both equations gave highly accurate fu_inc predictions for 62 drugs with comparable low bias, as shown in Fig. 3, A and B. Zidovudine and nilvadipine were the only exceptions, where both equations over-predicted the fu_inc value by more than 50%.

High lipophilicity (logP/D > 5). Both equations gave equally inaccurate fu_inc predictions for 14 compounds investigated, with an average under-estimation at high microsomal protein concentration of 159 and 131% for Austin and Hallifax, respectively (Table 3; Fig. 3).

Intermediate lipophilicity (logP/D = 2.5–5). This range of lipophilicity was the main focus of the current study, as the equations displayed a pronounced difference in this area (Fig. 1). Of the 51 drugs within this range, fu_inc values for 35 were predicted closer to the line of unity by the equation of Hallifax (Fig. 3). This equation estimated 53 to 82% of the fu_inc values within 1.5-fold of the predicted/observed ratio of 1 for 1.0 and 0.1 mg/ml, respectively. Especially high accuracy was observed in the fu_inc prediction for buspirone, quinidine, diazepam, and buprenorphine. The Austin equation estimated 22 to 73% of the fu_inc values within 1.5-fold of the predicted/observed ratio of 1 for 1.0 and 0.1 mg/ml, respectively. Particularly high accuracy was observed in the prediction of the fu_inc values for carvedilol, simvastatin, propafenone, and trimeprazine. For this range of lipophilicity, 9.8 to 55% of fu_inc estimates predicted by the Austin equation were outside 2-fold of the observed values, in contrast with 7.8 to 35% seen in the case of estimates obtained using the Hallifax equation (Fig. 3). Significant outliers were lorcainide and imipramine for the Austin equation, which were under-estimated by 600 and 700%, respectively, and felodipine and nicardipine for the Hallifax equation, which were over-estimated by 500 and 1000%, respectively. Over the entire range of lipophilicity, a lower bias was observed for the predictions obtained by the Hallifax equation compared with the Austin equation (Table 3).

Due to the differences seen between the predictive equations in the area of moderate lipophilicity, the impact of variability in logP estimates on fu_inc predictions was assessed (Fig. 4). A propagated 20% variation in the predictions of logP resulted in 50 and 15% variation of fu_inc using the equations of Austin and Hallifax, respectively, at a logP/D of 2.5. However, at the higher end of lipophilicity (logP = 5), 20% variation on logP resulted in 5.4- and 6.7-fold difference in the fu_inc prediction obtained by the Austin and Hallifax equations, respectively, at a microsomal protein concentration of 0.1 mg/ml, as illustrated in Fig. 4. The difference in the fu_inc prediction is even more pronounced if higher microsomal concentrations (1.0 mg/ml) are used, ranging from 10- to 21-fold in the case of the Austin and Hallifax equations, respectively, indicating caution in the use of predicted logP values.

Discussion

It has become widely accepted that the fraction of drug unbound in an incubation needs to be incorporated into the in vitro determination of clearance and inhibition potential to correct for nonspecific binding (Obach et al., 1997; Tucker et al., 2001; Margolis and Obach, 2003; Ito and Houston, 2005; Riley et al., 2005; Brown et al., 2006). In recent years, two prediction equations have been published to estimate fu_inc (Austin et al., 2002; Hallifax and Houston, 2006). This study was undertaken to identify the limitations within these empirical methods and to provide recommendation when the predictive equations can replace experimental fu_inc values with confidence. Consequently, the fu_inc values predicted by both equations were evaluated against experimentally determined fu_inc for a data set of 127 drugs (35 from the current study and 92 from the literature values) at three different microsomal protein concentrations and over a representative range of lipophilicity.

Sensitivity Analysis. In the area of low lipophilicity (logP/D ≤ 0), negligible interaction is expected with microsomal protein, resulting in fu_inc values of ∼1. The assumption that highly hydrophilic drugs interact minimally with microsomal proteins or phospholipids is met by the Austin equation. Due to the nonlinear nature of the Hallifax equation, the use of this equation was inappropriate in this area. The large discrepancy between the two equations highlighted at high microsomal protein concentration and lipophilicity (Fig. 1) indicated that reliance solely on the predicted fu_inc values is inadvisable in this particular area.

Impact of Microsomal Protein Concentration on the Prediction of fu_inc. The sensitivity analysis indicated that the microsomal protein concentration had less effect on the fu_inc predictions than the lipophilicity. This is particularly true at low microsomal protein concentrations. However, it still had a significant effect on the extent of binding observed; this effect increased at higher microsomal protein concentrations. The Austin equation showed a tendency to under-predict fu_inc values at all microsomal protein concentrations investigated in the current study (Table 3; Fig. 3). In contrast, the equation of Hallifax predicted the fu_inc values ≥ 0.4 with high accuracy but displayed particular problems in accurately predicting very highly lipophilic drugs where fu_inc ≤ 0.2 (Fig. 3). Comparison of prediction accuracy at different microsomal protein concentrations indicated that the use of the Hallifax equation for fu_inc predictions was advantageous, as shown in Fig. 3 and Table 3. Especially, fu_inc values at higher microsomal protein concentrations were better predicted using this equation.

Impact of Lipophilicity on the Prediction of fu_inc. The impact of lipophilicity was studied at microsomal protein concentrations from 0.1 to 1.0 mg/ml. This range of microsomal protein concentration is widely used for drug depletion profiles and inhibition studies (Obach, 1999; Jones and Houston, 2004; Galetin et al., 2005; Rawden et al., 2005; Riley et al., 2005; Brown et al., 2006; Galetin and Houston, 2006; Mohutsky et al., 2006; Obach et al., 2006).

Highly accurate and similar fu_inc predictions were obtained by both equations for low lipophilicity drugs (logP/D ≤ 2.5), which is in accordance with the sensitivity analysis, indicating that both prediction equations can be used interchangeably in this area of lipophilicity. At the same time, both equations failed equally in predicting the fraction unbound of highly lipophilic (logP/D ≥ 5) drugs. The poor correlation observed between experimental and predicted fu_inc for some of the drugs in this lipophilicity area (e.g., ritonavir and mibefradil) may be a result of incomparability of peak areas in the analytical assay as no linearity study was performed. This study did not investigate the accuracy of fu_inc predictions for drugs exceeding logP/D of 7 due to the low availability of such lipophilic drugs. As the precision in fu_inc predictions decreased with increasing lipophilicity in this data set, fu_inc predictions of very highly lipophilic drugs can be expected to be poor. In addition, as even minor variation in logP predictions/determination resulted in a substantial variation in fu_inc, the fraction unbound should be determined experimentally for drugs or new chemical entities with logP/D ≥ 5.

Special consideration was given to the intermediate lipophilicity (logP/D = 2.5–5), as the sensitivity analysis showed a significant difference in the predictions between the two equations. As a large number of drugs and potentially new chemical entities can be expected to be found within this lipophilicity range, further emphasis was placed on experimental determination of fu_inc values for compounds in this particular logP/D range. Twenty-two drugs from our own experiments and 29 from the literature (n = 51) were investigated in this lipophilicity range. On average, the Austin equation resulted in an under-estimation of fu_inc (118–185%), whereas the equation of Hallifax generally over-estimated (113–121%) the extent of nonspecific binding (Table 3). The Hallifax equation predicted a larger number of drugs closer to the line of unity, as indicated by a larger proportion of predictions within 1.5-fold of the observed values (Fig. 3).

The effect of using predicted (as opposed to the experimental) logP values, and of variability in those estimates, on the fu_inc predictions has also been investigated. Highly accurate logP predictions were obtained by three online software packages, Syracuse Research Corporation, ACD, and Interactive. The mean of these three software packages was found to be the most accurate to predict logP values for the data set investigated. A very good agreement was observed in particular for drugs with logP ≥ 2 (Fig. 2), whereas the prediction accuracy was lower at logP = 0–2. However, this was acceptable, as minimal interaction with microsomal protein is expected in this area of lipophilicity, as indicated by the sensitivity analysis. Still, even a relatively low bias in logP predictions may influence fu_inc predictions significantly, as lipophilicity was indicated as the most important parameter for fu_inc predictions. A propagation of a 20% variation in lipophilicity had a minor effect at low logP/D values (Fig. 4). However, with increasing lipophilicity, this effect became more pronounced, especially for the Hallifax equation, indicating caution in the use of predicted logP values in conjunction with fu_inc predictions. It is of concern that the inaccuracy in logP and consequently microsomal fu_inc prediction may be propagated further into hepatocyte studies, as it has been proposed that the extent of binding in hepatocyte incubations can be extrapolated from microsomal fu_inc estimates, assuming a correlation between microsomal and hepatocyte binding at 1 mg/ml and 10⁶ cells/ml, respectively (Austin et al., 2005).

In conclusion, the current analysis has highlighted the importance of drug lipophilicity as a very sensitive parameter for the prediction of the fu_inc. Both equations investigated showed very good agreement in the fu_inc estimates at low microsomal protein concentration, in particular for drugs with low lipophilicity. A significant difference in the fu_inc estimates was seen in the area of intermediate lipophilicity due to the nature of the prediction equations and their sensitivity on the variability in the logP estimates. On average, the Hallifax equation provided more accurate fu_inc predictions, in particular for lipophilic drugs (logP/D = 2.5–5) and at higher microsomal protein concentrations. The extent of nonspecific binding for highly lipophilic drugs was poorly predicted by both equations, suggesting that the fraction unbound should be determined experimentally for drugs with logP/D ≥ 5; this cutoff should be even lower (logP/D ≥ 3) if microsomal protein concentrations above 0.1 mg/ml are used. As overall prediction accuracy was the highest at low microsomal protein concentrations, it is prudent to perform kinetic and inhibition studies for new chemical entities at the lowest microsomal protein concentration possible.