Concomitant medications causing drug-drug interactions (DDIs) have led to serious adverse drug events during treatment and resulted in restrictions in prescribing drugs and withdrawal of drugs from the market (Jankel and Fitterman, 1993; Yuan et al., 1999). The incidence and extent of DDIs would be expected to increase when multiple inhibitors of a specific drug-metabolizing enzyme are administered simultaneously compared with administration of a single inhibitor alone. According to the U.S. Food and Drug Administration's Guidance for Industry Drug Interaction Studies, inhibitors of cytochrome P450 3A4 (CYP3A4) can be classified as potent, moderate, or weak if the area under the plasma concentration-time curve (AUC) fold increase of midazolam with the coadministered inhibitor is more than 5-fold, between 2- and 5-fold, or less than 2-fold, respectively (Guidance for Industry: In Vivo Drug Metabolism/Drug Interaction Studies: Study Design, Data Analysis, and Recommendations for Dosing and Labeling, U.S. Food and Drug Administration, 2006, http://www.fda.gov/cder). Thus, when two moderate inhibitors or one moderate and one weak inhibitor are given together, it is likely that they would act as a potent inhibitor. However, to date, studies on DDIs have been focused exclusively on the interactions between two drugs. It is not clear whether the extent of inhibition in the presence of multiple inhibitors is predictable from that of each inhibitor alone because predictive models of complex DDIs involving multiple inhibitors have not been evaluated.

CYP3A4 inhibition can be reversible and/or irreversible. Irreversible inhibition, also referred to as mechanism-based inhibition, is characterized by time- and inhibitor concentration-dependent loss of enzyme activity (Silverman, 1988). A mechanism-based inhibitor inhibits the enzyme through irreversible or quasi-irreversible binding to the enzyme; thus, the enzyme activity does not return immediately upon elimination of the inhibitor from plasma or tissue (Ito et al., 2003). Interestingly, many clinically significant CYP3A4 inhibitors have been shown to possess, to varying extents, both reversible and irreversible inhibitory effects on CYP3A4 (Zhou et al., 2004). However, whether both effects contribute to the overall extent of inhibition remains unclear.

In a compound mixture in which multiple mechanism-based inhibitors are present, their combined effect cannot be assumed to be simply additive because 1) competition between the inhibitors for the enzyme active site may modulate their inhibition effect and 2) inhibition of the metabolism of each other leads to a higher inhibitor concentration compared with that of each inhibitor alone. The ultimate outcome is determined by the interplay of these factors.

The primary objective of this work was to evaluate a model incorporating competition between the inactivators for the combined effects of multiple irreversible inhibitors. Two representative CYP3A4 inhibitors, the antimicrobial agent erythromycin (ERY) and the calcium channel blocker diltiazem (DTZ), with their major metabolites, N-desmethylerythromycin (nd-ERY) and N-desmethyldiltiazem (nd-DTZ), were chosen as clinically relevant examples to evaluate the model. DTZ and ERY are moderately strong inhibitors of CYP3A4 in vivo, causing an approximately 4-fold increase in the AUC of oral MDZ (Olkkola et al., 1993; Backman et al., 1994).

Materials and Methods

Chemicals and Reagents. Testosterone (TES), 6β-hydoxytestosterone (6β-OH TES), ERY, DTZ, N-desmethyldiazepam, and troleandomycin were purchased from Sigma-Aldrich (St. Louis, MO). nd-ERY was purchased from the U.S. Pharmacopoeia (Rockville, MD). nd-DTZ was a gift from Tanabe Seiyaku Co. (Osaka, Japan). NADPH (98%) was purchased from Roche Diagnostics (Indianapolis, IN). All other reagents were of high-performance liquid chromatography (HPLC) grade.

cDNA-Expressed Human CYP3A4 (+b₅) and Human Liver Microsome. cDNA-expressed CYP3A4 and cytochrome b₅ [rCYP3A4 (+b₅)] in insect cell membrane were purchased from BD Gentest (Woburn, MA). One adult human liver microsome (HLM) sample (IUL-72) was chosen from a liver bank prepared from human liver tissues obtained at surgery in accordance with protocols approved by the institutional review board of Indiana University–Purdue University Indianapolis/Clarian (Indianapolis, IN). Microsomal fractions were prepared as described by Gorski et al. (1994) and were kept at –80°C. The total protein concentration of the HLMs was 32 mg/ml (Lowry et al., 1951). The CYP3A4 and CYP3A5 protein concentrations were 25.3 and 0.6 pmol/mg of protein, respectively, as quantified by Western blot (Dennison et al., 2007). The CYP3A5 genotype of this human liver was *3/*3 as assessed by real-time reverse transcriptase-polymerase chain reaction as described previously (Dennison et al., 2007).

Quantitation of Reversible Inhibition of CYP3A4 by ERY, nd-ERY, DTZ, and nd-DTZ. To estimate the reversible inhibition constant, K_i, TES and inhibitors were incubated with rCYP3A4 (+b₅) (20 pmol) and HLMs (0.1 mg) in sodium phosphate buffer (0.1 M, pH 7.4) and NADPH (1 mM) at 37°C for 3 min. The enzyme reaction was terminated by adding 1 ml of ice-cold acetonitrile. TES concentrations over the range of 10 to 100 μM were used. Concentrations of inhibitors varied over the ranges of 5 to 50 μM (ERY), 5 to 50 μM (nd-ERY), 15 to 120 μM (DTZ), and 0.5 to 20 μM (nd-DTZ) for the incubations with rCYP3A4 (+b₅) and 25 to 200 μM (ERY and nd-ERY), 5 to 160 μM (DTZ), and 0.5 to 20 μM (nd-DTZ) for the incubations with HLMs. The 3-min incubation time was chosen to minimize enzyme inactivation during incubation so that the estimated K_i was considered to reflect primarily the binding affinity of the inhibitors to the enzyme.

The reversible inhibition constant K_i was estimated by fitting the appropriate inhibition models (competitive, noncompetitive, or uncompetitive) to the 6β-OH TES formation rate versus TES concentration data for the incubation for 3 min using nonlinear regression (WinNonlin 4.0; Pharsight, Mountain View, CA). Lineweaver-Burk plots (⅙β-OH TES formation rate versus 1/TES) were constructed to differentiate modes of inhibition.

Quantitation of Irreversible Inhibition of CYP3A4 by ERY, nd-ERY, DTZ, and nd-DTZ. TES 6β-hydroxylation was used as a marker reaction to quantify CYP3A4 activity. rCYP3A4 (+b₅) (20 pmol) or HLMs (1 mg) were preincubated in a 50-μl reaction mixture with various concentrations of each inhibitor in the presence of NADPH (1 mM) at 37°C for 0, 0.5, 1, and 2 min [rCYP3A4 (+b₅)] or 0, 1, 2, and 5 min (HLMs). After the preincubation, 950 μl of an incubation mixture containing TES and 1 mM NADPH in 0.1 M sodium phosphate buffer were transferred into the preincubation tube (to achieve a final TES concentration of 200 μM) and further incubated at 37°C for 5 min. The enzyme reaction was terminated by adding 1 ml of ice-cold acetonitrile. A saturating concentration (10 × K_m) of TES was used to measure the remaining catalytically active CYP3A. The inhibitor concentrations for preincubation with rCYP3A4 (+b₅) ranged from 1 to 50 μM for ERY, 1 to 50 μM for nd-ERY, and 0.5 to 15 μM for DTZ and nd-DTZ. The inhibitor concentrations for preincubation with HLMs ranged from 2.5 to 100 μM for ERY and nd-ERY, 2.5 to 20 μM for DTZ, and 0.5 to 15 μM for nd-DTZ.

To estimate the inactivation parameters, the natural logarithm of the percentage of the remaining CYP3A4 activity was plotted against the preincubation time. The observed pseudo first-order rate constants (k_obs) were determined from the slopes of the initial linear decline in activity. The parameters k_inact and K_I were obtained from simultaneous fitting of the data of the percentage of the remaining activity versus the preincubation time at all inhibitor concentrations using nonlinear regression (WinNonlin 4.0) according to the following equations: 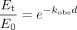where E_t and E₀ are enzyme activity at times 0 and t, respectively, k_obs is the inactivation rate constant at a given inactivator concentration, k_inact is the rate constant that defines the maximal rate of inactive enzyme formation, I is the initial concentration of the inhibitor, and K_I is the inhibitor concentration when k_obs = k_inact/2.

A Model for the Extent of Inactivation in the Presence of Multiple Inhibitors. The aim of this experiment was to evaluate the additive characteristic of a model for the prediction of the extent of inactivation by multiple mechanism-based inhibitors. For this purpose, a relatively strict condition (i.e., inactivation occurs during the initial linear phase, the inhibitor concentration stays constant, and no substrate is present) was applied to avoid confounding factors such as inhibitor depletion or nonlinear decrease of the enzyme activity. Equations X and Y, each generated from eq. 1, were first evaluated:

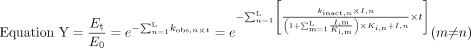
In eqs. X and Y, n refers to the number of different inhibitors (1–i) in the reaction mixture. In eq. Y, m represents all of the inhibitors other than the ith inhibitor, i.e., m ≠ n. In eq. X, the inactivation rate constant, k_obs, of each inhibitor was added to account for their combined effects. In eq. Y, K_I of each inhibitor was further modified by 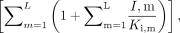where I, _m and K_{i, m} are the concentration and competitive inhibition constant of the coexisting inhibitors, respectively, assuming that the inhibitors will compete with each other for the enzyme active site. The percentage of remaining enzyme activity in eqs. X and Y was calculated from the estimated inhibition parameters (k_inact, K_I, and K_i) for each inhibitor alone, inhibitor concentrations, and the preincubation times.

To test eqs. X and Y, inhibitors were incubated in combination (ERY + DTZ, ERY + nd-ERY, DTZ + nd-DTZ, and all four compounds together) at concentrations equal to ½K_I, K_I, and 2K_I of each inhibitor for 1 and 2 min with rCYP3A4 (+b₅) and 2 and 5 min with HLMs. The percentage of remaining enzyme activity was measured as described above. The brief incubation time was used because eqs. X and Y follow the same assumption as eq. 1; i.e., the reactions under the initial linear range and the inhibitor depletion were minimal. The predicted and observed percentages of remaining enzyme activity were compared for eqs. X and Y.

Time Course of CYP3A Inactivation. To quantify the percentage of remaining CYP3A activity and the inhibitor and metabolite concentrations with time, rCYP3A4 (+b₅) (20 pmol) and HLMs (1 mg) were incubated with ERY, nd-ERY, DTZ, and nd-DTZ, alone and in combination, for a period of 10 min. For each time point, two identical tubes were prepared. At 0, 0.5, 1, 2, 5, and 10 min after the initiation of the reaction, 950 μl of incubation mixture containing TES (to achieve a final TES concentration of 200 μM) and 1 mM NADPH in 0.1 M sodium phosphate buffer were transferred into one tube to estimate the remaining enzyme activity. The other tube was quenched with 1 ml of ice-cold acetonitrile for the measurement of the inhibitor and metabolite concentrations at the specified time points. Vehicle controls (i.e., no inhibitors) were run to account for any decrease in enzyme activity with time under these conditions. Experiments were performed in duplicate.

Predictive Models for a Compound Mixture Containing the Substrate and Multiple Inhibitors. A more general situation for DDIs (both in vitro and in vivo) is that the substrate coexists with the inhibitor in a reaction mixture and the inhibitor and substrate may coexist for a period of time that is longer than the initial linear phase of enzyme inactivation. Therefore, eqs. X and Y were further tested in an incubation for 10 min, which is out of the initial linear phase and in the presence of the substrate, TES. TES and inhibitor concentrations used for the 10-min incubation with a single inhibitor were the same as those used for the 3-min incubation. For the incubations of TES with multiple inhibitors, a concentration at its K_m in each enzyme system was used. The formation rate of 6β-OH TES was measured as described earlier.

The following three candidate models incorporating reversible (model A) or irreversible (model B) inhibition or both (model C), were evaluated for the prediction of inhibition of CYP3A4 activity by single or multiple inhibitors: 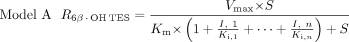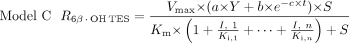In these models, V_max, K_m, and S are the maximal rate and the Michaelis-Menten constant for 6β-OH TES formation and TES concentration, respectively. In model A, I is the nominal inhibitor concentration, assuming no inhibitor depletion during competitive inhibition. In models B and C, a time-averaged inactivator concentration () was used to represent the true inhibitor concentration in the mixture due to possible inhibitor depletion during a 10-min incubation. was calculated by eq. 8 where AUC_0–10 is the area under the inhibitor concentration-time curve from 0 to 10 min estimated with noncompartment analysis using the trapezoidal rule in WinNonlin. The time averaged inhibitor concentration was calculated by dividing this AUC by 10 min:

In models B and C, only eq. Y was incorporated for the loss of enzyme of activity due to mechanism-based inhibition by single or multiple inhibitors because preliminary studies suggested that eq. Y better predicted the remaining enzyme activity than eq. X did. Furthermore, because a preliminary study showed a biexponential decrease of enzyme activity during the incubation of 10 min and eq. Y can account only for the initial linear phase, a second term was incorporated as shown in eq. 9, where a, b, and c were estimated by curve-stripping of the plot of the percentage of remaining enzyme activity against time: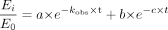

In models A, B, and C, V_max and K_m of TES were estimated by incubating TES at various concentrations with rCYP3A4 (+b₅) and HLMs for 5 min and fitting the 6β-OH TES formation rate versus TES concentration data to a Michaelis-Menten equation. When there was substrate present, S/K_m was also included in the term that modified the K_I of each inhibitor. S was TES concentration. The value of K_m estimated was used as the K_i for TES.

Quantitation of 6β-OH TES, ERY, nd-ERY, DTZ, and nd-DTZ by HPLC and Liquid Chromatography/Mass Spectrometry. The 6β-OH TES concentration was determined by an HPLC system with ultraviolet detection at a wavelength of 254 nm as described previously (Zhao et al., 2002). For the determination of ERY and nd-ERY concentrations, 200 μl of internal standard (0.5 ng/μl troleandomycin in 1 M sodium cabonate-1 M sodium bicarbonate, 4:1 v/v, pH = 9.6) was added to each sample, followed by the addition of 3 ml of hexane/ethyl acetate (1:1 v/v). Chromatographic separation of the analytes and internal standard was accomplished with a Phenomenex Luna C18 column (3 μm × 2 mm i.d. × 150 mm). The mobile phase consisted of a mixture of acetonitrile-methanol-ammonium acetate (0.25 M, pH = 7.6) (200:75:225 v/v/v) and was pumped at a flow rate of 0.2 ml/min. The effluent was delivered to a mass spectrometer (Navigator; Thermo Fisher Scientific, Waltham, MA) interfaced with a Hewlett Packard 1100 binary pump equipped with an HP1100 autosampler. The electrospray ionization probe was run in the positive ion mode with probe temperatures of 300°C. ERY, nd-ERY, and troleandomycin were detected in the selected ion recording mode at m/z 734, 720, and 771, respectively.

The concentrations of DTZ and nd-DTZ were determined on the basis of a previous method with modification (Gorski et al., 1999). In brief, the reaction mixture was extracted with 8 ml of ethyl acetate after the addition of 0.5 ml of 0.5 M sodium hydroxide-glycine buffer (pH = 8.5) Chromatographic separation of the analytes and internal standard was accomplished with a Phenomenex Luna C18 column (5 μm × 4.6 mm i.d. × 150 mm). The mobile phase consisted of a mixture of methanol-100 mM ammonium acetate (75:25 v/v) and was pumped at a flow rate of 1 ml/min. The effluent was delivered to a mass spectrometer (Navigator) interfaced with a Hewlett Packard 1100 binary pump equipped with an HP1100 autosampler. The electrospray ionization probe was run in the positive ion mode with a probe temperature of 400°C. DTZ, nd-DTZ, and N-desmethyldiazepam were detected in the selected ion recording mode at m/z 414, 401, and 271, respectively.

Data Analysis. Percent mean error (%ME) and percent mean absolute error (%MAE) were calculated as follows and served as measures of bias and precision, respectively, for the predictions: 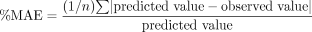where n is the number of predictions.

A two-tailed Student's t test was performed to compare the %ME and %MAE calculated for different models. Differences were considered statistically significant at P < 0.05.

Results

Reversible and Irreversible Inhibition of CYP3A4 by ERY, nd-ERY, DTZ, and nd-DTZ. All four compounds (ERY, DTZ, nd-ERY, and nd-DTZ) displayed time- and concentration-dependent inhibition of CYP3A4 with rCYP3A4 (+b₅) and HLMs, with the major metabolite of ERY, nd-ERY, being characterized as a mechanism-based inhibitor for the first time (Fig. 1). Figure 2 shows the plots of k_obs against inhibitor concentrations for all four compounds with rCYP3A4 (+b₅) and HLMs. The estimated k_inact and K_I for CYP3A4 were obtained by fitting the inactivation profiles to eq. 1 and are summarized in Table 1. The values of K_I and k_inact estimated with rCYP3A4 (+b₅) were approximately 3-fold lower and 4-fold higher than those estimated with HLMs, respectively, for all four compounds. On the basis of the ratio of k_inact/K_I, the inactivation efficiency of nd-ERY is comparable to that of ERY (k_inact/K_I values for nd-ERY and ERY are 60 and 70 min^–1 mM^–1 in rCYP3A4 (+b₅), and 9 and 6 min^–1 mM^–1 in HLMs, respectively), whereas nd-DTZ appears to be more potent than DTZ (k_inact/K_I = 1333 and 220 min^–1 mM^–1 for nd-DTZ and DTZ with rCYP3A4+b₅, and 133 and 20 min^–1 mM^–1 with HLMs, respectively).

• Download figure
• Open in new tab
• Download powerpoint

Fig. 1.

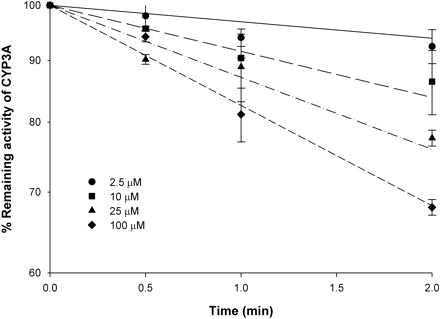
Plot of percentage of remaining CYP3A4 activity against preincubation time for nd-ERY incubation with HLM. nd-ERY at 2.5 μM (•), 10 μM (▪), 25 μM (▴), and 100 μM (♦) was incubated with HLMs (1 mg) in a 50-μl reaction mixture in the presence of NADPH (1 mM) at 37°C for 0, 1, 2, and 5 min. The remaining enzyme activity was quantified by adding 950 μl of incubation mixture containing 200 μM TES and further incubating at 37°C for 5 min. Individual data points represent the mean result from duplicate incubations. Error bars are S.D. The lines represent the simultaneous fit of data at all inhibitor concentrations.

To evaluate reversible inhibition, each compound was incubated with TES in rCYP3A4 (+b₅) and HLMs for 3 min. The 3-min incubation time was chosen to minimize enzyme inactivation during incubation so that the estimated K_i was considered to reflect primarily the binding affinity of the inhibitors to the enzyme. All four compounds displayed competitive inhibition of CYP3A4 (data not shown). ERY and nd-ERY have comparable values of K_i (Table 2). DTZ appears to be a more efficient competitive inhibitor of CYP3A4 with rCYP3A4 (+b₅) (K_i = 5.9 μM) than with HLMs (K_i = 41 μM), and nd-DTZ is a potent competitive inhibitor of CYP3A4 with both systems with K_i approaching K_I (Table 2).

The effect of incubation time on K_i estimation was evaluated. Compared with the K_i values estimated with the 3-min incubation, the K_i values estimated with the 10-min incubation are generally smaller, as illustrated in Table 2. Figure 3 shows the Lineweaver-Burk plot for 3- and 10-min incubation of TES and nd-DTZ with rCYP3A4 (+b₅). The fitted lines for different inhibitor concentrations converged on the y-axis for the 3-min incubation, suggesting competitive inhibition. In contrast, for the 10-min incubation, the intercept on the y-axis, which represents 1/V_max, is higher for higher nd-DTZ concentrations. This result is probably due to more significant time-dependent inactivation by nd-DTZ occurring during the 10-min incubation than during the 3-min incubation.

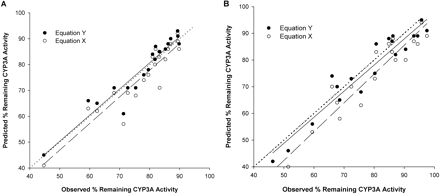
Model for the Extent of Inactivation in the Presence of Multiple Inhibitors. Equations X and Y were first evaluated in an incubation of the inhibitors (in the absence of substrate) with CYP3A4 for a brief incubation time to ensure that inactivation occurred within the initial linear phase. The predicted percentage of remaining enzyme activity calculated using eqs. X and Y was plotted against the observed percentage of remaining enzyme activity obtained from experiments for the combination of ERY + DTZ, ERY + nd-ERY, DTZ + nd-DTZ, and all four compounds together with rCYP3A4+ (+b₅) and HLMs. Figure 4 shows the plots for ERY + DTZ (Fig. 4A) and DTZ + nd-DTZ (Fig. 4B) with HLMs. Overall, good correlation was observed for both combinations using eqs. X and Y, with eq. Y having a better predictive performance. For example, for ERY + DTZ with HLMs, the %ME, an indicator of the closeness of the predicted values to the observed values, was significantly lower using eq. Y than eq. X (0.008 ± 0.06 versus –0.08 ± 0.06, p < 0.05) (Table 3); for DTZ + nd-DTZ, the %ME was –0.02 ± 0.06 and –0.08 ± 0.08 using eqs. X and Y, respectively, p < 0.05) (Table 3). The %ME was significantly lower using eq. Y than eq. X (p < 0.05) for all of the other predictions, as listed in Table 3. The %MAE, an indicator of the precision of the prediction, was similar in most cases for using both equations, indicating comparable precision.

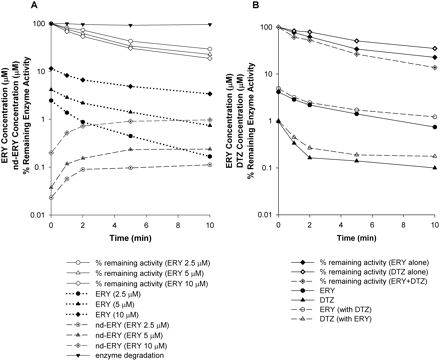
Changes in the Percentage of Remaining Enzyme Activity, Parent Drug, and Metabolite Concentrations with Time.Figure 5A shows the time profiles for percentage of remaining enzyme activity, inhibitor and metabolite concentrations, and enzyme degradation after incubation of ERY at 2.5, 5, and 10 μM (i.e., at 1/2K_I, K_I, and 2K_I) with rCYP3A4 (+b₅) for 10 min. The 10-min incubation reveals a biexponential decrease in the percentage of the remaining enzyme activity at all three ERY concentrations. There was an initial rapid decline within the first 2 min followed by a slower decrease phase up to 10 min. A similar pattern was observed for the 10-min incubation of other compounds in both systems. Also, the ERY concentration-time profile showed significant depletion of ERY with rCYP3A4 (+b₅) at later time points with ERY concentrations falling from 2.5, 5, and 10 μM to 0.17, 0.74, and 3.4 μM, respectively. Furthermore, the decline in the ERY concentrations was approximately in parallel with the decline in enzyme activity. An early rapid depletion of ERY was accompanied by the appearance of nd-ERY. At the lower ERY concentrations, the concentrations of nd-ERY appeared to reach a plateau for all three ERY concentrations tested. The time profiles of percentage of remaining enzyme activity and inhibitor concentrations after the incubation of multiple inhibitors were also investigated. As shown in Fig. 5B, when 5 μM ERY and 1 μM DTZ [i.e., at their respective K_I values in rCYP3A4 (+b₅)] were incubated together, there was a further decrease in the percentage of remaining enzyme activity compared with that for each inhibitor alone at all time points. With eq. 8, the time-averaged ERY concentrations in the absence and presence of DTZ were 1.7 and 2 μM, respectively, and the time-averaged DTZ concentration increased from 0.2 to 0.27 μM when there was ERY present in the incubation. These increases in the inhibitor concentrations resulted in insignificant changes in the percentage of remaining enzyme activity using eqs. X and Y or models A, B, and C (data not shown).

• Download figure
• Open in new tab
• Download powerpoint

Fig. 2.

Plots of k_obs against inhibitor concentration of ERY (•) and nd-ERY (○) in rCYP3A4 (+b₅) (A) and HLMs (B) and DTZ (•) and nd-DTZ (○) in rCYP3A4 (+b₅) (C) and HLMs (D). k_obs value estimated from the slope of the initial linear decline phase of the percentage of remaining CYP3A4 activity against preincubation time plot for each inhibitor concentration was plotted against inhibitor concentration. Each point represents the mean of duplicate samples. The solid and broken lines represent the predicted k_obs values using the estimates of the parameters from the simultaneous fits (eq. 1) for parent drugs and metabolites, respectively.

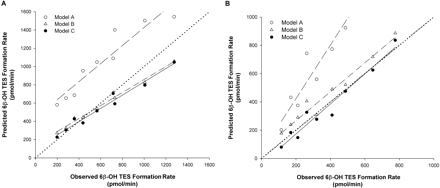
Prediction of the Interactions between TES and Multiple Inhibitors Considering Reversible and Irreversible Inhibition. To further test the additive model in the context of a compound mixture containing inhibitors and substrate incubated for a longer period of time (10 min), inhibitors (alone and in combination) and TES were incubated with rCYP3A4 (+b₅) and HLMs for 10 min. The V_max and K_m (mean ± S.D.) estimated for 6β-OH TES formation were 2650 ± 10.9 pmol/min and 28 ± 1 μM with rCYP3A4 (+b₅) and 286 ± 8.4 pmol/min and 58.6 ± 1.2 μM with HLMs. Figure 6 shows the representative plots of the predicted versus observed 6β-OH TES formation rate for the incubation of TES with ERY (Fig. 6A) and TES with nd-DTZ (Fig. 6B) for 10 min with rCYP3A4 (+b₅) using models A, B, and C. For ERY, model A (competitive inhibition model) overestimated the 6β-OH TES formation rate (i.e., underestimated the extent of inhibition by ERY), whereas the predicted and observed 6β-OH TES formation rates were in good agreement using either model B or C (%ME was 0.93, 0.06, and –0.01 for models A, B, and C, respectively). In contrast, both models A and B underestimated the inhibition of 6β-OH TES formation by nd-DTZ, whereas the observed 6β-OH TES formation rate was excellently predicted by model C, suggesting that both reversible and irreversible inhibition needs to be considered, especially for compounds that also exhibit strong reversible inhibition. The %ME (mean ± S.D.) was significantly higher for model A than for model C and for model B than for model C (1.00 ± 0.38, 0.26 ± 0.21, and –0.07 ± 0.19 for models A, B, and C, respectively). The %ME and %MAE values calculated for the three models for all of the predictions are listed in Table 4. Overall, the 6β-OH TES formation rate was best predicted by model C for all compounds (%ME for model C was the lowest and was significantly lower than that for model A for all the predictions as indicated by the p values). Model B significantly overestimated the 6β-OH TES formation rate for all the incubations tested except for ERY and nd-ERY with both enzyme systems.

• Download figure
• Open in new tab
• Download powerpoint

Fig. 3.

Lineweaver-Burk plot for the inhibition of CYP3A4 by nd-DTZ in an incubation for 3 min (A) and 10 (B) min. TES (10–100 μM) and nd-DTZ at 0, 0.5, 2, and 6 μM were incubated with rCYP3A4 (+b₅) (20 pmol) at 37°C for 3 and 10 min. The lines are the best fit of data at each inhibitor concentration.

• Download figure
• Open in new tab
• Download powerpoint

Fig. 4.

Plot of predicted against observed percentage of remaining enzyme activity for the incubation of combination of ERY + DTZ (A) and DTZ + nd-DTZ (B) with HLMs using eq. X (○) and eq. Y (•). The predicted percentage of remaining enzyme activity was calculated by eqs. X and Y. The observed percentage of remaining enzyme activity was measured from incubation of ERY and DTZ or DTZ and nd-DTZ with HLMs (1 mg) for 2 and 5 min. Inhibitor concentrations were ½K_I, K_I, and 2K_I. The dotted line, solid line, and broken line represent the line of identity, regression line for data using eq. Y, and regression line data using eq. X, respectively.

• Download figure
• Open in new tab
• Download powerpoint

Fig. 5.

Percentage of remaining enzyme activity, ERY concentration, and nd-ERY concentration in incubation of ERY at various concentrations with rCYP3A4 (+b₅) for 10 min (A) and percentage of remaining enzyme activity and inhibitor concentrations in incubation of ERY alone, DTZ alone, and ERY and DTZ together with rCYP3A4 (+b₅) for 10 min (B). In A, ERY was incubated at 2.5, 5, and 10 μM. In B, ERY and DTZ were incubated at 5 and 1 μM, respectively.

• Download figure
• Open in new tab
• Download powerpoint

Fig. 6.

Plot of predicted against observed 6β-OH TES formation rate in the incubation of TES with ERY (A) and nd-DTZ (B) with rCYP3A4 (+b₅) for 10 min using model A (○), model B (▵), and model C (•). Concentrations used for the incubations were 10, 20, and 40 μM for TES, 2.5, 5, and 10 μM for ERY, and 0.25, 0.5, 2, and 6 μM for nd-DTZ. The dotted line, dashed line, dashed-dotted line, and solid line represent the line of identity and regression line for data using model A, B, or C, respectively.

Figure 7 shows the representative plots of the predicted against observed 6β-OH TES formation rates for the incubation of TES and the combination of ERY + DTZ (Fig. 7A) and TES and ERY + DTZ + nd-ERY + nd-DTZ (Fig. 7B) with HLMs. The predicted versus observed 6β-OH TES formation rates agreed the best with each other using model C for both combinations. As also shown in Table 4, the %ME was significantly lower for model C than for model A or B for the prediction of all the combinations, indicating that model C had the best predictive performance among the three models.

Discussion

DDIs remain a serious problem in clinical practice and the development of new drugs (Lazarou et al., 1998; Gandhi et al., 2003). Predictive models for complex DDIs involving multiple inhibitors and their metabolites are not readily available, making it infeasible to predict in vivo DDIs involving multiple inhibitors from in vitro data. In the current study we evaluated for the first time an interaction model for the combined effect of multiple inhibitors on CYP3A4 inhibition in vitro. The combined effect of multiple inhibitors can be well predicted by the additive model (eq. Y), in which the inactivation rate constant of each inhibitor was added and the competition between coexisting inhibitors was considered. The results in this study also suggest that simultaneous reversible and irreversible inhibition effects need to be taken into account (model C) in a compound mixture involving multiple inhibitors and their metabolites. Furthermore, characterization of the biexponential decline of the remaining enzyme activity in an incubation with a mechanism-based inhibitor was shown to be important for prediction, although the mechanism underlying this phenomenon remains unclear.

Because of the dual effect of a mechanism-based inhibitor as a competitive inhibitor and an inactivator of the enzyme, reversible and irreversible inhibition parameters were first estimated separately for all of the four compounds under optimal experimental conditions (i.e., the measurement of the inactivation effect was not obscured by the competitive inhibition effect and vice versa). The widely adopted approach for mechanism-based inhibition consists of a “preincubation” stage followed by an “incubation” stage (Silverman, 1988). However, efforts have not always been exerted to meet the two important assumptions (that there is negligible metabolism of the inhibitor during the “preincubation” stage and that negligible enzyme inactivation occurs during the “incubation” stage) to ensure the accuracy in parameter estimation (Yang et al., 2005). Considerable ranges of preincubation time and dilution factors have been used across laboratories, leading to great discrepancies in the estimates of the inactivation parameters (Ghanbari et al., 2006). Our study was designed to minimize the preincubation and incubation times and maximize the dilution factor. Specifically, a brief preincubation time (2 min for rCYP3A4 (+b₅) and 5 min for HLM), a relatively high dilution factor (20-fold), and a short incubation time (5 min) were applied in this study. Similarly, for the estimation of the competitive inhibition constant, K_i, the incubation time was kept brief (3 min) so that the estimated K_i values were considered to reflect primarily the initial binding of the inhibitor to the enzyme with minimal inactivation occurring. The differences in the K_i values estimated using data from the 3- and 10-min incubations (Table 2; Fig. 3) further confirmed the impact of incubation time on the estimation of this parameter. Moreover, the Lineweaver-Burk plot suggested competitive inhibition of 6β-OH TES formation by nd-DTZ in the 3-min incubation, indicating that no significant inactivation occurred during the 3-min incubation. Thus, the estimation of K_i using a 3-min incubation was considered appropriate. In contrast, the intercepts on the y-axis were higher for higher nd-DTZ concentrations with the 10-min incubation, suggesting lower V_max at a higher inhibitor concentration, probably due to enzyme inactivation occurring with time. Caution should be exerted with differentiating inhibition patterns using the Lineweaver-Burk plot alone, because the plot for the 10-min incubation could be misinterpreted as noncompetitive or uncompetitive inhibition (Fig. 3).

• Download figure
• Open in new tab
• Download powerpoint

Fig. 7.

Plot of predicted against observed 6β-OH TES formation rate in the incubation of TES with ERY + DTZ (A) and ERY + DTZ + nd-ERY + nd-DTZ (B) with HLMs for 10 min using model A (○), model B (▵), and model C (•). Concentrations used for the incubations were 40 μM for TES, 5, 15, and 75 μM for ERY, 5, 10, and 40 μM for DTZ, 15 and 75 μM for nd-ERY, and 0.5 and 1 μM for nd-DTZ. The dotted line, dashed line, dashed-dotted line, and solid line represent the line of identity and regression line for data using model A, B, or C, respectively.

A simple rearrangement of eq. X shown in eq. 12 suggests that eq. X actually reflects the fact that the percentage of remaining enzyme activity in the presence of two inhibitors can be predicted by the product of the percentage of remaining activity of each inhibitor alone: 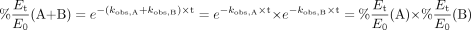Nevertheless, it is not surprising that eq. X overestimated the extent of inhibition for all of the combinations tested in both rCYP3A4 and HLMs (Fig. 4; Table 3). A major reason for this discrepancy is most likely competition between inhibitors that is not considered. After the K_I of each inhibitor was modified by (1 + ΣI/K_i) of all the coexisting inhibitors, the prediction performance was significantly improved for all of the combinations tested. On the other hand, in a reaction mixture of two inhibitors, one would expect that mutual inhibition of the metabolism of each other may lead to an increase in the concentrations of each inhibitor, which in turn, may enhance the inhibition effect compared with that of each inhibitor alone. However, as shown in Fig. 5, when ERY and DTZ were incubated together at their K_I values, the concentrations of ERY (or DTZ) in the presence and absence of DTZ (or ERY) are comparable. This result was also observed at other concentrations of inhibitors tested (½K_I and 2K_I). To this end, eq. Y was proven to be an appropriate model for the combined effect of multiple inhibitors.

Equation Y was further evaluated under conditions in which the substrate and inhibitor(s) were added simultaneously to the reaction mixture and incubated for 10 min (exceeding the initial linear phase). For this purpose, the change in the percentage of remaining enzyme activity and inhibitor and metabolite concentrations with time during a 10-min incubation was examined. Figure 5 indicates a biexponential decline in the percentage of remaining enzyme activity throughout the 10-min incubation. Because the commonly used equation for mechanism-based inhibition (eq. 1) is only valid for the initial linearly declining phase, there would be significant overestimation of the extent of inhibition if eq. 1 was applied for the whole 10-min incubation. However, the factors that might cause the subsequent slower phase are not yet clear. Preliminary data in our laboratory suggest that it is not likely to be due to the decrease in inhibitor concentrations (data not shown). Therefore, a descriptive model was applied for the second phase as shown in eq. 9, where a, b, and c were constants estimated by curve-stripping of the percentage of remaining enzyme activity versus time plot. The significant depletion of the inhibitor at later time points is consistent with other observations and is probably due to the inhibitor being either complexed with the enzyme through metabolic intermediate complex formation or converted to the metabolite (Zhao et al., 2005; McGinnity et al., 2006). However, there was a failure to achieve mass balance with an accounting of the measured metabolite (nd-ERY) and the loss of enzyme activity because of the irreversible ERY binding, suggesting that other metabolites formed (data not shown).

Furthermore, the relative contribution of reversible and irreversible inhibition was studied for the incubation of a mechanism-based inhibitor with the substrate. Figure 6 shows the predicted versus observed 6β-OH TES formation rate when ERY (Fig. 6A) or nd-DTZ (Fig. 6B) was incubated with TES. For a drug such as ERY, which acts as an effective mechanism-based inhibitor but weak reversible inhibitor, the competitive inhibition model (model A) significantly underestimated the inhibition extent, whereas results with the inactivation model (model B) were generally close to those with the model that incorporates simultaneous reversible and irreversible inhibition (model C) at the concentrations tested (½K_I, K_I, and 2K_I), indicating that inactivation is what mainly occurred in the reaction mixture. In contrast, for nd-DTZ, which represents the group of compounds that are effective as both reversible and irreversible inhibitors, both model A and model B underestimated the inhibition extent. Therefore, as a whole, model C was considered to be the best model for a mechanism-based inhibitor that exhibits either high or low potency as a reversible inhibitor. On the other hand, model C incorporating eq. Y best estimated 6β-OH TES formation rate in a mixture in which TES was incubated with multiple inhibitors simultaneously, further suggesting the validity of the interaction model (eq. Y).

Prediction of the magnitude of in vivo DDIs using in vitro inhibition data has been a routine strategy applied to reduce the number of in vivo studies required and to guide the design of clinical trials (Ito et al., 1998). This strategy has been successful for single inhibitor interaction for many cases (Obach et al., 2006, 2007). With the validation of the additive model in this study, prediction of the extent of inhibition with multiple inhibitors has been made possible. This is of particular importance because clinical studies for all possible combinations of inhibitors are not feasible.

Consistent with previous findings, the K_I and K_i estimated with rCYP3A4 (+b₅) were generally lower and the k_inact was higher than those estimated with HLMs (Tables 1 and 2) in this study (McConn et al., 2004). A possible explanation is higher nonspecific protein binding and a different lipid environment in HLMs compared with those in a recombinant enzyme system. Interestingly, McGinnity et al. (2006) reported that the inhibition parameters (k_inact and K_I) estimated in cultured primary human hepatocytes generally were in good agreement with the values derived using HLMs. Thus, caution should be exercised when one is making predictions of the extent of in vivo DDIs using parameters estimated from recombinant enzymes.

To summarize, nd-ERY and ERY have comparable inhibition potency, whereas nd-DTZ is more potent than DTZ as a CYP3A4 inhibitor. The additive model incorporating competition between inhibitors (eq. Y) is appropriate for the prediction of the extent of inhibition in the presence of multiple inhibitors. Moreover, simultaneous reversible and irreversible inhibition effects should be taken into account in a reaction mixture of multiple inhibitors and a substrate of CYP3A4.