Advertisement
Research ArticleArticle

Kinetic Modeling of Steady-State Situations in Cytochrome P450 Enzyme Reactions

F. Peter Guengerich
Drug Metabolism and Disposition November 2019, 47 (11) 1232-1239; DOI: https://doi.org/10.1124/dmd.119.088732

Abstract

In the course of investigations of the kinetics of individual reactions of cytochrome P450 (P450) enzymes, a number of points about the complexity of P450 enzyme kinetics have become apparent. Several of these are of particular relevance to work with P450 enzymes in the course of drug development and lead optimization, particularly with regard to estimating in vitro kinetic parameters and dealing with enzyme inhibitors. Modern simulation modeling has been applied to situations involving issues of preincubation time with moderate strength and strong inhibitors, inhibition by tightly bound ligands that have been identified in P450 enzymes, extensive substrate depletion, P450 reactions with a rate-limiting step after product formation, and the consumption of an inhibitor during a reaction by either a P450 enzyme being monitored or another one in a mixture. The results all follow from first principles, and simulations reveal the extent of their significance in various settings. The order of addition of substrate and inhibitors can change the apparent outcome (inhibition constant, Ki), and the effect of the order is more pronounced with a stronger inhibitor. Substrate depletion alters parameters (Michaelis constant, Km) and can generate apparently sigmoidal plots. A rate-limiting step after product formation lowers the apparent Km and distorts Ki. Consumption of an inhibitor during a reaction affects Ki and differs depending on which enzyme is involved. The results are relevant with P450 enzymes and other enzymes as well.

SIGNIFICANCE STATEMENT Kinetic simulations have been used to address several potential problems in enzyme kinetic analysis. Although the simulations done here are general for enzyme reactions, several problems addressed here are particularly relevant to cytochrome P450 reactions encountered in drug development work.

Introduction

Many in vitro assays are performed with human cytochrome P450 enzymes in the course of modern drug development (Zhang et al., 2008; Pearson and Wienkers, 2019). The approach has been highly successful, in general, in allowing extrapolation of parameters to generate estimates of in vivo pharmacokinetics (Polasek et al., 2018; Wakayama et al., 2018). Another major goal of in vitro work is with P450 inhibitors, largely in the context of predicting drug-drug interactions (Rodrigues and Lin, 2001; Wienkers and Heath, 2005; McGinnity et al., 2008; Guest et al., 2011; Guengerich, 2019).

However, there are several issues with the design of in vitro experiments, the meaning of individual kinetic parameters, and the interpretation of what some parameters really mean. One parameter of considerable interest is kcat/Km (or Vmax/Km), termed the specificity constant by biochemists (Johnson, 2003, 2019) and in vitro clearance (Clint) by pharmacologists. There are also issues in the evaluation of inhibition results, not only time-dependent (mechanism-based) but even the simpler pure competitive inhibition.

In the course of our kinetic studies with several human P450 enzymes, we have been using kinetic modeling/fitting software, including KinSim (Bell and Guengerich, 1997), DynaFit (Guengerich et al., 2002), and most recently KinTek Explorer (Chowdhury et al., 2010; Guengerich et al., 2019a,b; Reddish and Guengerich, 2019). Most of our work has been done in fitting experimental data, but the software can also be very useful in modeling possible outcomes of experimental situations, sometimes leading to a preferred approach.

Several issues could potentially be considered, but these were the five areas investigated: 1) the effect of the order of mixing substrate and inhibitor with an enzyme, including the length of preincubation time, 2) the effect of a very tightly bound ligand on enzyme kinetics, 3) the effect of substrate depletion, 4) the effect of a rate-limiting step after product formation, and 5) issues related to changes in inhibitor concentration due to biotransformation by the same enzyme or another in a mixture (e.g., microsomes). The modeling is generic for enzymes but highly relevant to P450 enzymes.

Materials and Methods

All kinetic simulations were performed in KinTek Explorer software (version 8.0; KinTek Corp., Snow Shoe, PA) using an Apple iMac OSX 10.13.6 system. GraphPad Prism v. 8.0 (GraphPad, San Diego, CA) was used for some of the fitting: plots of rates or products formation versus substrate concentration (specifically Fig. 2C, Fig. 3C, Fig. 4, B and C, Fig. 5B, Fig. 6D, and Fig. 8C).

The system used in all simulations was a two-stage mixing model (Supplemental Figs. 1–8). The enzyme E was present in the first time component (t1 step), with or without an inhibitor, with this “preincubation” time (t1) varying as described. The enzyme (E) was then mixed (t2 step) with multiple concentrations of substrates (S), and the product (P) was monitored as a function of time (generally 180 seconds = 3 minutes). The substrate, enzyme, inhibitor concentrations, and reaction time were selected to reflect typical values that might be encountered in assays in the pharmaceutic industry.

All steady-state Ki values were calculated using a simple competitive inhibition equation (Segel, 1975):Embedded ImageMost values are rounded to two significant digits.

Results

General Design of Simulations.

Rates of binding of molecules to enzymes were generally set to 106 M−1 s−1 (1 µM s−1). This value is in the range of values we have measured for human P450 enzymes (Guengerich et al., 2019b). (Multiphasic binding is simplified here for the modeling.) This rate constant is in the range generally accepted for enzyme-ligand binding (Schreiber et al., 2009); higher rates (e.g., 108–109 M−1 s−1) usually result from the influence of charges (Fersht, 1999; Zang et al., 2005; Schreiber et al., 2009; Guengerich et al., 2019b).

The final enzyme concentration in the assay was generally set to 0.05 µM, which is realistic in the context of many sensitive assays done today using liquid chromatography with mass spectrometry methods, much less than earlier assays done with colorimetric assays (e.g., 1 to 2 µM) (Guengerich, 2014). Most of the simulations were done with a range of substrate concentrations varying from 0.5 to 100 µM. The modeling also focused on Ki values in the range of 1 nM–10 µM, which are likely to be of most concern with P450 enzymes in drug development.

Effects of Preincubation Time with Inhibitors.

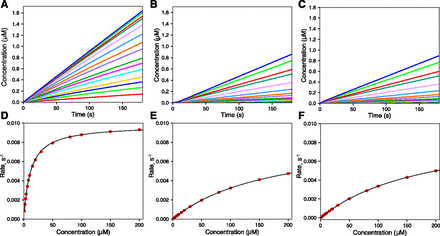
The first model used a Ki inhibitor (I) (1 µM) with with a 0.1 µM Kd value (Fig. 1). When there was no preincubation period (i.e., I was added along with S to start the reaction), a brief faster reaction was seen (most easily at the highest S concentration) before the reaction was linear (Fig. 1B). However, when the preincubation was performed with the inhibitor present for 120 seconds (Fig. 1C), there was a noticeable lag phase before the substrate displaced the inhibitor and the steady-state (linear reaction) occured (again, most easily seen at the highest concentration).

Fig. 1.
Fig. 1.

Effect of preincubation time with an enzyme inhibitor. The kinetic model consisted of:

StepReactionk+k−Kd
1E + S ⇄ ES1 µM−1 s−110 s−110 µM
2ES → EP0.1 s−1—
3EP ⇄ E + P2 s−11 µM−1 s−12 µM
4E + I ⇄ EI1 µM−1 s−10.1 s−10.1 µM

with [E] = 0.1 µM mixed with [S] = 1, 2, 3, 4, 6, 7, 10, 15, 20, 30, 50, 80, 100, 150, and 200 µM, to yield final concentrations of one-half of these (see Supplemental Information). (A) No inhibitor added. (B) [I] = 2 µM added in preincubation for 0.1 seconds. (C) [I] = 2 µM added in preincubation for 120 seconds, final [I] = 1 µM after mixing to initiate the reaction. The following parameters were estimated in each part:

Partkcat (s−1)Km,(app) (µM)Ki (µM)
A0.009711.5—
B0.00981900.064
C0.00891750.071

In the two analyses (Fig. 1, B and C), the respective kcat values were 0.0098 seconds and 0.0089 s−1 (compared with 0.0097 s−1 in the uninhibited reaction). The respective Ki values (in Fig. 1, B and C) were 0.064 and 0.071 µM, both only slightly lower than the Kd of 0.1 µM set for I in the model.

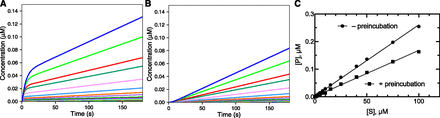
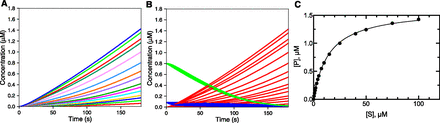
The effect of preincubation time and order was also examined with a 10-fold stronger inhibitor (Kd 10 nM set in model). The “burst” (Fig. 2A) and lag (Fig. 2B) were clearly observable and are more pronounced than in Fig. 1, as might be expected. The patterns shown in Fig. 2A were very similar to the reactions in which the rate-limiting step occured after product formation (as discussed later). As in Fig. 1, time is needed for either the inhibitor to replace the substrate and act (Fig. 2A) or for the substrate to replace the inhibitor (Fig. 2B) and be acted upon by the enzyme.

Fig. 2.
Fig. 2.

Effect of preincubation time and a strong enzyme inhibitor. The kinetic model was the same as in Fig. 1, except that k−4 was 0.01 s−1 (Kd 10 nM). I was added at 2 µM for a final concentration of 1 µM in the reaction. (A) Zero preincubation time with inhibitor before adding substrate. (B) Preincubation time of 30 seconds before adding substrate. (C) Final product concentrations after 180 seconds produced in parts A (●) and B (▪). In part C, the slope of the linear fit plot derived without preincubation was 0.00269 ± 0.00003 (S.E.M.), r2 0.9986; and the slope of the linear fit plot derived with preincubation was 0.00167 ± 0.00002 (S.E.M.), r2 0.9978.

The rates in these reactions could not be accurately fit by linear extrapolations (especially Fig. 2A), so the concentration of product measured at 180 seconds reaction time (3 minutes) was used as a surrogate of the rate. This measurement would correspond to a value determined by liquid chromatography with tandem mass spectrometry typically measured in such a kinetic screen. The plots (vs. [S]) are not saturating in either case (Fig. 2C), in keeping with the very low Ki (which could not be estimated by the usual criteria; see Materials and Methods). It should be noted that the rates ([P] formation) measured after preincubation with the inhibitor present (120 seconds) will ultimately reach those with the inhibitor added at the same time as the substrate but not within the 180-second reaction time.

A conclusion of the modeling presented here is that, in general, preincubation with both substrate and inhibitor is preferred, particularly if the inhibitor is tightly bound. In robotic systems, this design should be incorporated. If crude systems are used (e.g., microsomes), it is conceivable that the order of addition might be influenced by the instability of an inhibitor, such as an esterase substrate (see the section Issues with Consumption of an Inhibitor during Incubations for that case).

Effect of a Very Tightly Bound Ligand on Reaction Rates.

The general concept of a very tightly bound inhibitor was examined. This case corresponds to recombinant P450 enzymes that are purified but still contain a ligand. Several examples of such behavior have been reported, including fatty acids in P450 2C8 (Schoch et al., 2004) and bacterial P450 119A1 (Krest et al., 2013) and indole in P450 2A13 (Smith et al., 2007). Although the cited publications regarding these preparations were of interest due to structural or mechanistic aspects, the point we have addressed is that catalytic assays would be very problematic.

A related concern is purified P450 preparations that have been prepared in the presence of strong ligands to stabilize the enzyme during expression or purification, such as family 1A P450 enzymes (Sandhu et al., 1994; Sansen et al., 2007; Wang et al., 2011). With these enzymes, the presence of residual inhibitor may have to be critically analyzed to permit careful studies on catalysis or inhibition. Although they are not generally considered to be high affinity, nonionic detergents (Hosea and Guengerich, 1998) and ionic steroidal detergents (Hobler et al., 2012; Reddish and Guengerich, 2019) may be present in P450 enzymes and produce artifacts of this nature.

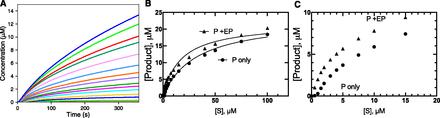
In this model, a Kd of 1 nM was arbitrarily set, with [E] = 0.05 µM and one inhibitor present (in the t2 phase, after 2-fold dilution of enzyme to start the reaction, i.e., [E] = 0.10 µM in t1 phase). The quadratic analysis indicated that ∼90% of the enzyme would be bound to I, so the simulation was initiated with a mixture of 0.09 µM [EI], 0.01 µM [E]free, and 0.01 µM [I]free in the t1 phase. The rate plots were concave upward, due to the time required for the substrate to replace I (Fig. 3A). Although the linear fits (Fig. 3A) were not perfect, the results yielded a reasonable hyperbolic plot versus [S] (Fig. 3B). A more accurate inhibition plot was seen when [P] (at 180 seconds) was plotted versus [S] (Fig. 3C). In the latter analysis, the Km apparent was 16 µM, and Ki was estimated to be 71 nM, two orders of magnitude greater than the set Kd for I (1 nM).

Fig. 3.
Fig. 3.

Effect of a very tightly bound ligand on an enzyme reaction. The model used in Fig. 1 was applied, without any preincubation. Here, [I] was set equal to [E], 0.1 µM, both diluted to 0.05 µM in the reaction. At this concentration of [E] and [I] and Kd for the EI complex set at 1 nM (k−4 = 0.001 µM in model for Fig. 1), a quadratic equation indicates that ∼90% of the E is bound as EI, so the reaction began with [EI] = 0.09 µM, [E]free = 0.01 µM, and [I]free = 0.01 µM, mixed with substrate. (A) Time course of reaction at varying substrate concentration. (B) Plot of apparent line fits of rates (part A) versus [S]. (C) Final concentration of product P formed in part A (●) compared with uninhibited reaction ([I] = 0) (Fig. 1A), fit to Michaelis-Menten plot. In part C the kcat,apparent was 0.0015 s−1 (compared with 0.0097 s−1 in Fig. 1A), Km,apparrent was 16 µM, and KI was estimated to be 71 nM (compare with k−4/k5 = 1 nM in the model setup). The r2 values were 0.9997 for the uninhibited reaction and 0.9998 for the inhibited reaction.

Interestingly, kcat was also only 15% of the value obtained in the absence of inhibitor, although this model is one involving competitive inhibition.

Effects of Substrate Depletion.

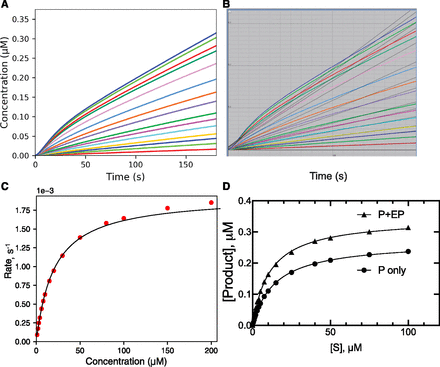
We also used same basic model (Fig. 1) but with the final enzyme concentration ([E]) increased 40-fold (to 2 µM) to run the reaction at lower substrate concentrations to completion (Fig. 4A). As expected, in the reactions at lower [S] all of the substrates had been converted to product; even with the higher substrate concentrations, the reactions were no longer linear.

Fig. 4.
Fig. 4.

Effect of long reaction time and substrate depletion on kinetic parameters. The starting concentration of [E] was raised to 4 µM (final [E] = 2 µM). (A) Plot of [P] versus time at varying substrate concentrations. (B) [P] at 180 seconds plotted versus [S] (● [P] only, ▲ [P] + [EP]). (C) Expansion of plot from part B in low [S] region. The Km,apparent values were 64 µM for P only and 34 µM for P + EP. In part B, the r2 values (hyperbolic fit) were 0.9783 for [P] + [EP] and 0.9947 for [P] only. In part C, the r2 value (Hill equation, sigmoidal fit) was 0.9978 for [P] only.

The plots (Fig. 4A) did not fit well to linear equations, so product formation ([P]) at t = 180 seconds was plotted versus [S] (Fig. 4B). As expected, the plot was not saturating, but a Km value of 64 µM could be estimated (6.4-fold > Kd). When enzyme-bound product (EP) was included, the totals were expectedly higher (Fig. 4B), and a Km of 34 µM was estimated.

When the initial phase of the reaction was plotted, the results with [P] generated an apparent sigmoidal curve (Fig. 4C). Many reports of Hill plots with low n values (1.1–1.5) have been reported in the literature, especially for P450 3A4, including some of our own (Ueng et al., 1997; Korzekwa et al., 1998; Fowler et al., 2002; Frank et al., 2011). Analysis of the [P]-only data (Fig. 4B) yielded a Hill n value of 1.11 (95% confidence interval [CI], 1.05–1.17). Use of only the [P] points shown in Fig. 4C yielded n = 1.42 (CI, 1.37–1.47) (and S50 = 40 µM). However, when the sum of [E] + [EP] is considered, the sigmoidicity is lost (Fig. 4C).

The extent to which this phenomenon is responsible for weak Hill plots in the literature is unknown, in that few describe details of reaction conditions. If the sum of [EP] + [P] is considered, then even running reactions to completion cannot give a sigmoidal curve, at least in the simplest case, in that doubling [S] can only double ([P] + [EP]) and a linear fit will be seen (Fig. 4C).

In practice, running an assay in which the reaction was quenched with a solvent (or acid) to release the enzyme-bound product would yield P + EP (Fig. 4, B and C) and solve the problem. However, in a continuous spectrophotometric (or fluorimetric) assay this would not be the case, and the caveats could apply.

Issues with a Rate-Limiting Step after Product Formation.

This is a classic situation seen in enzyme kinetics (Walsh, 1979) and has also been identified in some P450 reactions. It is best documented in the cases of oxidation of ethanol and acetaldehyde by P450 2E1 (Bell and Guengerich, 1997; Bell-Parikh and Guengerich, 1999), but less definitive cases have also been reported such as toluene (rat liver microsomes, P450 unknown) (Ling and Hanzlik, 1989) and 18-hydroxycorticosterone (bovine P450 11B1) (Imai et al., 1998).

Such reactions are characterized by burst kinetics (Fig. 5A), with the sharpness of the burst depending upon the relative rates of individual reaction steps. In the modeling in Fig. 5A, step 3 was reduced to 0.02 s−1 (10-fold). Such plots are usually fit to v = Ae−k1t + kss [S], where A is a constant, kss is a steady-state rate, and k1 is an exponential (Johnson, 2003). A linear fit of Fig. 5A is not possible, and [P] at 180 seconds was used as before (Fig. 5B).

Fig. 5.
Fig. 5.

Effect of a rate-limiting step after product formation. The basic model in Fig. 1 was used, except k3 was reduced to 0.02 s−1 (10-fold). (A) Plots of product formation versus Time at varying concentrations of substrate. (B) Plots of product formation versus [S] for [P] only (●) and the sum of [P] + [EP] (▲). The Km value for P only was 4.0 µM, and the Km for (P + EP) was 2.1 µM (compared with Kd = 10 µM for S in model). In part C, the r2 values (hyperbolic fit) were 0.9835 for [P] + [EP] and 0.9820 for [P] only.

As expected, the sum ([EP] + [P]) was higher than [P] in that much of the product remained bound. The kcat value was ∼20% of that observed when k3 = 2 s−1 (Fig. 3C) although the rate constant had been reduced 10-fold. The estimated Km was 4.0 µM when only [P] was considered and was 2.1 µM when both [P] and [EP] were considered, compared with Kd = 10 µM for binding substrate in the model. The relationship Km < Kd is a classic phenomenon when product release is rate limiting (Walsh, 1979; Guengerich et al., 2003).

Another issue is the nature of competitive inhibition when the rate-limiting step follows product formation (Fig. 6). The model used in Fig. 5 was used with [I] = 1 µM, and the Kd of I was set at 0.1 µM (with a preincubation time of 120 seconds) (Fig. 6A). The burst character is still obvious, at least at the higher substrate concentrations. Although linear fits of the traces were less than ideal (Fig. 6B), the rate plots generated a hyperbolic fit (Fig. 6C), with kcat = 0.0019 s−1 and Km,apparent 21 µM, yielding Ki = 0.95 µM. The plot of [P] (t = 180 seconds) versus [S] gave a Km,apparent value of 11 µM, yielding Ki = 0.23 µM. These Ki values differ and can be compared with the Kd of 0.1 µM set in the model.

Fig. 6.
Fig. 6.

Inhibition of an enzyme with a slow step after product formation. The model of Fig. 5 (Fig. 1 with k3 = 0.02 s−1) was used with [I] = 1 µM, k4 = 1 µM−1 s−1, and k−4 = 0.1 second−1 (Kd for I = 0.1 µM). The preincubation time with I was 120 seconds. (A) Plot of [P] versus Time. (B) Linear fits to curves in part A. (C) Rate versus [S] (rates from part B). (D) Plots of total product formed after 180 seconds versus [S]: [P] only (●) and [P] + [EP] (▲). The kcat was 0.0019 s−1, Km,apparent was 21 µM, and Ki was 0.95 µM (compared with Kd = 0.1 µM in model). In part C, the r2 values (hyperbolic fit) were 0.9999 for [P] + [EP] and 0.9992 for [P] only.

Issues with Consumption of an Inhibitor during Incubations.

One issue with an enzyme inhibitor is that it is also a molecule and subject to reaction. This can manifest in a role as a competitive inhibitor—that is, to be transformed (to a noninhibitory molecule) by the enzyme under investigation. A model was developed in which the enzyme reacted with the inhibitor (I) at the same rate as the substrate (S) and was then released from the enzyme (step 5 in Fig. 7). The result of the transformation of the inhibitor can be seen in comparing Fig. 7, B and C. The course of the disappearance of I is shown in Fig. 7D, with less inhibitor being removed at higher concentrations of the substrate due to competition. In this model, the calculated Ki was 0.13 µM without inactivation of I (Fig. 7B) but rose to 0.70 µM in Fig. 7C when it was transformed (compare Kd of 0.10 µM for I set in the model). For this, kcat was nearly identical in all situations (Fig. 7).

Fig. 7.
Fig. 7.

Effect of consumption of inhibitor by an enzyme. The basic model of Fig. 1 was used, with Step 5 added in Part C.

StepReactionk+k−Kd
1E + S ⇄ ES1 µM−1 s−110 s−110 µM
2ES → EP0.1 s−1—
3EP ⇄ E + P2 s−11 µM−1 s−12 µM
4E + I ⇄ EI1 µM−1 s−10.1 s−10.1 µM
5EI → E + X0.10

(A) Plot of P versus Time at varying concentrations of X. (B) Same as in part A but with [I] = 2 µM in Premix, k5 = 0. (C) Same as in Part B but with k5 = 0.1 s−1 (same as k2). No correction was made for a product of I binding to E. (D) Time course of [P] (red), [I] (green), and [EI] during reaction (in part C). (E) The v versus [S] plot for part A. (F) The v versus [S] plot for part B. (G) The v versus [S] plot for part C. The following parameters were estimated:

Partkcat (s−1)Km,apparent (µM)KiKd(S)Kd(I)
A0.009810.6—10—
B0.00901870.13—0.10
C0.0089300.70—0.10

Another situation occurs with mixtures of P450 enzymes in microsomes when an inhibitor of one P450 is being oxidized by another P450; for instance, quinidine is an inhibitor of P450 2D6 but a substrate for P450 3A4 (Guengerich et al., 1986). Such a model was set up, with a second enzyme (F) transforming I as rapidly as E transforms S (Fig. 8). As in Fig. 7C, there is curvature in the plots of [P] versus time, as I is removed from inhibiting E, but the degree is more marked (Fig. 8A). A plot of the course of I during the reaction shows only a limited effect of S on the course of I, as expected and in contrast to Fig. 7D (Fig. 8B). A hyperbolic plot of [P] (at t = 180 seconds) versus [S] yielded kcat = 0.0089 s−1 (near the uninhibited value) and KI = 5.2 µM, 52-fold > Kd for I (0.1 µM) (Fig. 8C).

Fig. 8.
Fig. 8.

Effect of consumption of an inhibitor by a different enzyme in a mixture.

The model used was adapted from Figs. 1 and 7,

StepReactionk+k−Kd
1E + S ⇄ ES1 µM−1 s−110 s−110 µM
2ES → EP0.1 s−1—
3EP ⇄ E + P2 s−11 µM−1 s−12 µM
4E + I ⇄ EI1 µM−1 s−10.1 s−10.1 µM
5F + I ⇄ FI1 µM−1 s−10.1 s−10.10 µM
6FI → F0.1 s−10

where F is a second enzyme that does not interact with S. [E] = [F] = 0.1 µM in mixing (final concentration 0.05 µM). No premixing time was allowed to avoid consumption of I. (A) Plots of [P] versus time at varying values of [S]. (B) Time courses of [P], [I], and [EI] during course of reaction. (C) Plot of [P] formed at t = 180 seconds versus [S]. Calculations from part C yielded kcat 0.0089 s−1 (compare with 0.0098 s−1 in Fig. 7A, without inhibition), Km,apparent = 14.7 µM, and Ki = 5.2 µM (compare with Kd of 0.1 µM for I in model). (Linear fits to Part A were poor but yielded kcat = 0.0089 s−1, Kd,apparent = 85 µM, and Ki = 0.89 µM.) In Part C, the r2 value (hyperbolic fit) was 0.9996.

Discussion

Several relevant scenarios related to P450 enzymes were examined by modeling. The results all follow from first principles, but some of the findings may not be so obvious, particularly for individuals who are not acquainted with enzyme kinetics. Modeling using modern software allows ready prediction of some issues in kinetics.

One aspect not dealt with here but highly relevant is the use of a relatively new approach to fitting actual v versus S plots—that is, Michaelis-Menten kinetics. The original publication (Michaelis and Menten, 1913, 2013; Michaelis et al., 2011) did not estimate Km directly, as was done by Lineweaver and Burk (1934) and elsewhere. It can be argued, and I definitely agree, that the two major parameters in steady-state enzyme kinetics are kcat (Vmax) and kcat/Km (Northrop, 1998), the latter of which Johnson terms ksp (specific constant) (Johnson, 2019).

Mathematically, the error is reduced in using a program to solve for kcat and ksp (kcat/Km)—and then deriving Km from the quotient. The process can easily be performed in GraphPad Prism software using the equationEmbedded Imagewhich we now do routinely in this laboratory. The error (e.g., S.D.) is reduced in all cases compared with calculating kcat and Km and then dividing. However, this approach was not used in this study because all the data are synthetic (modeling).

The issue of the correct prediction of Ki may or may not be an issue in predicting enzyme inhibition. Very weak and very strong inhibitions are easy to spot regardless of the assays; however, in borderline cases, providing the most accurate Ki (or at least EC50) may be critical to correct prediction, even with only competitive inhibition.

The simulations presented in this study are relatively simple, with an enzyme only binding to a single substrate (S) or inhibitor (I), and the rate constants for binding and release of S, I, and product (P) varying. However, P450 reactions can be much more complex. Heterotropic cooperativity (i.e., activation) was recognized nearly 50 years ago (Wiebel et al., 1971; Buening et al., 1978; Huang et al., 1981) and homotropic cooperativity ≥25 years ago (Guengerich et al., 1994; Shou et al., 1994; Ueng et al., 1997). Such allosteric phenomena are now generally attributed to multiple occupancy (Dabrowski et al., 2002; Schoch et al., 2004; Ekroos and Sjögren, 2006; Sohl et al., 2008; Muller et al., 2015), which can have varying effects.

Multiple occupancy, which makes kinetic simulations—and data fitting (Sohl et al., 2008)—much more complex, is beyond the scope of the modeling presented here. Moreover, the more complex a mechanism, the more ambiguous is the validity of a fit. Further, recent work has shown the relevance of conformational selection—and possibly induced fit—in the substrate promiscuity of P450 enzymes (Guengerich et al., 2019a,b). Again, modeling all the details of complex P450 reactions is beyond the scope of this work, which is intended as a relatively simple primer on some issues encountered in practical drug metabolism.

In summary, we have made the following conclusions. The order of addition of substrate and inhibitors can change the apparent outcome (inhibition constant Ki), and the effect of the order is more pronounced with a stronger inhibitor. Substrate depletion alters parameters (Michaelis constant Km) and can generate apparently sigmoidal plots. A rate-limiting step after product formation lowers the apparent Km and distorts Ki. Consumption of an inhibitor during a reaction affects Ki and differs depending on which enzyme is involved. This work may facilitate the design and interpretation of better high-throughput assays in drug development, and these approaches can be applied readily to issues with assays of other enzymes.

Acknowledgments

Thanks are extended to Dr. M. J. Reddish for implementation of the formula for calculating ksp and to K. Trisler for assistance in preparation of the manuscript.

Authorship Contributions

Participating in research design: Guengerich.

Conducted experiments: Guengerich.

Contributed new reagents or analytic tools: Guengerich.

Performed data analysis: Guengerich.

Wrote of contributed to the writing of the manuscript: Guengerich.

Footnotes

Abbreviations

CI
confidence interval
E
enzyme
EP
enzyme-bound product
I
inhibitor
kcat
maximum velocity for an enzyme reaction
Kd
dissociation constant
Ki
inhibition constant
Km
Michaelis constant (substrate value at which half-maximal velocity is achieved)
P
product
P450 (or CYP)
cytochrome P450
S
substrate

References

  1. ↵
    1. Bell LC and
    2. Guengerich FP
    (1997) Oxidation kinetics of ethanol by human cytochrome P450 2E1. Rate-limiting product release accounts for effects of isotopic hydrogen substitution and cytochrome b5 on steady-state kinetics. J Biol Chem 272:29643–29651.
    OpenUrlAbstract/FREE Full Text
  2. ↵
    1. Bell-Parikh LC and
    2. Guengerich FP
    (1999) Kinetics of cytochrome P450 2E1-catalyzed oxidation of ethanol to acetic acid via acetaldehyde. J Biol Chem 274:23833–23840.
    OpenUrlAbstract/FREE Full Text
  3. ↵
    1. Buening MK,
    2. Fortner JG,
    3. Kappas A, and
    4. Corney AH
    (1978) 7,8-Benzoflavone stimulates the metabolic activation of aflatoxin B1 to mutagens by human liver. Biochem Biophys Res Commun 82:348–355.
    OpenUrlCrossRefPubMed
  4. ↵
    1. Chowdhury G,
    2. Calcutt MW, and
    3. Guengerich FP
    (2010) Oxidation of N-nitrosoalkylamines by human cytochrome P450 2A6: sequential oxidation to aldehydes and carboxylic acids and analysis of reaction steps. J Biol Chem 285:8031–8044.
    OpenUrlAbstract/FREE Full Text
  5. ↵
    1. Dabrowski MJ,
    2. Schrag ML,
    3. Wienkers LC, and
    4. Atkins WM
    (2002) Pyrene.pyrene complexes at the active site of cytochrome P450 3A4: evidence for a multiple substrate binding site. J Am Chem Soc 124:11866–11867.
    OpenUrlCrossRefPubMed
  6. ↵
    1. Ekroos M and
    2. Sjögren T
    (2006) Structural basis for ligand promiscuity in cytochrome P450 3A4. Proc Natl Acad Sci USA 103:13682–13687.
    OpenUrlAbstract/FREE Full Text
  7. ↵
    1. Fersht A
    (1999) Structure and Mechanism in Protein Science, pp 158–161, Freeman, New York.
  8. ↵
    1. Fowler SM,
    2. Taylor JM,
    3. Friedberg T,
    4. Wolf CR, and
    5. Riley RJ
    (2002) CYP3A4 active site volume modification by mutagenesis of leucine 211. Drug Metab Dispos 30:452–456.
    OpenUrlAbstract/FREE Full Text
  9. ↵
    1. Frank DJ,
    2. Denisov IG, and
    3. Sligar SG
    (2011) Analysis of heterotropic cooperativity in cytochrome P450 3A4 using α-naphthoflavone and testosterone. J Biol Chem 286:5540–5545.
    OpenUrlAbstract/FREE Full Text
  10. ↵
    1. Guengerich FP
    (2014) Analysis and characterization of enzymes and nucleic acids relevant to toxicology, in Hayes’ Principles and Methods of Toxicology (Hayes AW and Kruger CL eds) pp 1905–1964, CRC Press/Taylor & Francis, Boca Raton, FL.
  11. ↵
    1. Guengerich FP
    (2019) Inhibition of drug metabolizing enzymes, in Handbook of Drug Metabolism (Pearson P and Wienkers L eds) pp 222–249, CRC Press/Taylor & Francis, Boca Raton, FL.
  12. ↵
    1. Guengerich FP,
    2. Kim B-R,
    3. Gillam EMJ, and
    4. Shimada T
    (1994) Mechanisms of enhancement and inhibition of cytochrome P450 catalytic activity, in Proceedings of the 8th International Conference on Cytochrome P450: Biochemistry, Biophysics, and Molecular Biology (Lechner MC ed), pp 97–101, John Libbey Eurotext, Paris, France.
  13. ↵
    1. Guengerich FP,
    2. McCormick WA, and
    3. Wheeler JB
    (2003) Analysis of the kinetic mechanism of haloalkane conjugation by mammalian θ-class glutathione transferases. Chem Res Toxicol 16:1493–1499.
    OpenUrlCrossRefPubMed
  14. ↵
    1. Guengerich FP,
    2. Miller GP,
    3. Hanna IH,
    4. Sato H, and
    5. Martin MV
    (2002) Oxidation of methoxyphenethylamines by cytochrome P450 2D6. Analysis of rate-limiting steps. J Biol Chem 277:33711–33719.
    OpenUrlAbstract/FREE Full Text
  15. ↵
    1. Guengerich FP,
    2. Müller-Enoch D, and
    3. Blair IA
    (1986) Oxidation of quinidine by human liver cytochrome P-450. Mol Pharmacol 30:287–295.
    OpenUrlAbstract
  16. ↵
    1. Guengerich FP,
    2. Wilkey CJ,
    3. Glass SM, and
    4. Reddish MJ
    (2019a) Conformational selection dominates binding of steroids to human cytochrome P450 17A1. J Biol Chem 294:10028–10041.
    OpenUrlAbstract/FREE Full Text
  17. ↵
    1. Guengerich FP,
    2. Wilkey CJ, and
    3. Phan TTN
    (2019b) Human cytochrome P450 enzymes bind drugs and other substrates mainly through conformational-selection modes. J Biol Chem 294:10928–10941.
    OpenUrlAbstract/FREE Full Text
  18. ↵
    1. Guest EJ,
    2. Rowland-Yeo K,
    3. Rostami-Hodjegan A,
    4. Tucker GT,
    5. Houston JB, and
    6. Galetin A
    (2011) Assessment of algorithms for predicting drug-drug interactions via inhibition mechanisms: comparison of dynamic and static models. Br J Clin Pharmacol 71:72–87.
    OpenUrlCrossRefPubMed
  19. ↵
    1. Hobler A,
    2. Kagawa N,
    3. Hutter MC,
    4. Hartmann MF,
    5. Wudy SA,
    6. Hannemann F, and
    7. Bernhardt R
    (2012) Human aldosterone synthase: recombinant expression in E. coli and purification enables a detailed biochemical analysis of the protein on the molecular level. J Steroid Biochem Mol Biol 132:57–65.
    OpenUrlCrossRefPubMed
  20. ↵
    1. Hosea NA and
    2. Guengerich FP
    (1998) Oxidation of nonionic detergents by cytochrome P450 enzymes. Arch Biochem Biophys 353:365–373.
    OpenUrlCrossRefPubMed
  21. ↵
    1. Huang MT,
    2. Johnson EF,
    3. Muller-Eberhard U,
    4. Koop DR,
    5. Coon MJ, and
    6. Conney AH
    (1981) Specificity in the activation and inhibition by flavonoids of benzo[a]pyrene hydroxylation by cytochrome P-450 isozymes from rabbit liver microsomes. J Biol Chem 256:10897–10901.
    OpenUrlAbstract/FREE Full Text
  22. ↵
    1. Imai T,
    2. Yamazaki T, and
    3. Kominami S
    (1998) Kinetic studies on bovine cytochrome p45011 beta catalyzing successive reactions from deoxycorticosterone to aldosterone. Biochemistry 37:8097–8104.
    OpenUrlCrossRefPubMed
  23. ↵
    1. Johnson KA
    (2003) Introduction to kinetic analysis of enzyme systems, in Kinetic Analysis of Macromolecules A Practical Approach (Johnson KA ed) pp 1–18, Oxford University Press, Oxford, UK.
  24. ↵
    1. Johnson KA
    (2019) New standards for collecting and fitting steady state kinetic data. Beilstein J Org Chem 15:16–29.
    OpenUrlCrossRefPubMed
  25. ↵
    1. Korzekwa KR,
    2. Krishnamachary N,
    3. Shou M,
    4. Ogai A,
    5. Parise RA,
    6. Rettie AE,
    7. Gonzalez FJ, and
    8. Tracy TS
    (1998) Evaluation of atypical cytochrome P450 kinetics with two-substrate models: evidence that multiple substrates can simultaneously bind to cytochrome P450 active sites. Biochemistry 37:4137–4147.
    OpenUrlCrossRefPubMed
  26. ↵
    1. Krest CM,
    2. Onderko EL,
    3. Yosca TH,
    4. Calixto JC,
    5. Karp RF,
    6. Livada J,
    7. Rittle J, and
    8. Green MT
    (2013) Reactive intermediates in cytochrome p450 catalysis. J Biol Chem 288:17074–17081.
    OpenUrlAbstract/FREE Full Text
  27. ↵
    1. Lineweaver H and
    2. Burk D
    (1934) The determination of enzyme dissociation constants. J Am Chem Soc 56:658–666.
    OpenUrlCrossRef
  28. ↵
    1. Ling KHJ and
    2. Hanzlik RP
    (1989) Deuterium isotope effects on toluene metabolism. Product release as a rate-limiting step in cytochrome P-450 catalysis. Biochem Biophys Res Commun 160:844–849.
    OpenUrlCrossRefPubMed
  29. ↵
    1. McGinnity DF,
    2. Waters NJ,
    3. Tucker J, and
    4. Riley RJ
    (2008) Integrated in vitro analysis for the in vivo prediction of cytochrome P450-mediated drug-drug interactions. Drug Metab Dispos 36:1126–1134.
    OpenUrlAbstract/FREE Full Text
  30. ↵
    1. Michaelis L and
    2. Menten ML
    (1913) Die Kinetik der Invertinwirkung. Biochem Z 49:333–369.
    OpenUrl
  31. ↵
    1. Michaelis L,
    2. Menten ML,
    3. Johnson KA, and
    4. Goody RS
    (2011) The original Michaelis constant: translation of the 1913 Michaelis-Menten paper. Biochemistry 50:8264–8269.
    OpenUrlCrossRefPubMed
  32. ↵
    1. Michaelis L and
    2. Menten MM
    (2013) The kinetics of invertin action. 1913. FEBS Lett 587:2712–2720.
    OpenUrl
  33. ↵
    1. Müller CS,
    2. Knehans T,
    3. Davydov DR,
    4. Bounds PL,
    5. von Mandach U,
    6. Halpert JR,
    7. Caflisch A, and
    8. Koppenol WH
    (2015) Concurrent cooperativity and substrate inhibition in the epoxidation of carbamazepine by cytochrome P450 3A4 active site mutants inspired by molecular dynamics simulations. Biochemistry 54:711–721.
    OpenUrl
  34. ↵
    1. Northrop DB
    (1998) On the meaning of Km and V/K in enzyme kinetics. J Chem Educ 75:1153–1157.
    OpenUrlCrossRef
  35. ↵
    1. Pearson PG and
    2. Wienkers LC
    (2019) Handbook of Drug Metabolism, CRC Press, Bocca Raton, FL.
  36. ↵
    1. Polasek TM,
    2. Shakib S, and
    3. Rostami-Hodjegan A
    (2018) Precision dosing in clinical medicine: present and future. Expert Rev Clin Pharmacol 11:743–746.
    OpenUrl
  37. ↵
    1. Reddish MJ and
    2. Guengerich FP
    (2019) Human cytochrome P450 11B2 produces aldosterone by a processive mechanism due to the lactol form of the intermediate 18-hydroxycorticosterone. J Biol Chem (294):12975–12991.
  38. ↵
    1. Rodrigues AD and
    2. Lin JH
    (2001) Screening of drug candidates for their drug—drug interaction potential. Curr Opin Chem Biol 5:396–401.
    OpenUrlCrossRefPubMed
  39. ↵
    1. Sandhu P,
    2. Guo Z,
    3. Baba T,
    4. Martin MV,
    5. Tukey RH, and
    6. Guengerich FP
    (1994) Expression of modified human cytochrome P450 1A2 in Escherichia coli: stabilization, purification, spectral characterization, and catalytic activities of the enzyme. Arch Biochem Biophys 309:168–177.
    OpenUrlCrossRefPubMed
  40. ↵
    1. Sansen S,
    2. Yano JK,
    3. Reynald RL,
    4. Schoch GA,
    5. Griffin KJ,
    6. Stout CD, and
    7. Johnson EF
    (2007) Adaptations for the oxidation of polycyclic aromatic hydrocarbons exhibited by the structure of human P450 1A2. J Biol Chem 282:14348–14355.
    OpenUrlAbstract/FREE Full Text
  41. ↵
    1. Schoch GA,
    2. Yano JK,
    3. Wester MR,
    4. Griffin KJ,
    5. Stout CD, and
    6. Johnson EF
    (2004) Structure of human microsomal cytochrome P450 2C8. Evidence for a peripheral fatty acid binding site. J Biol Chem 279:9497–9503.
    OpenUrlAbstract/FREE Full Text
  42. ↵
    1. Schreiber G,
    2. Haran G, and
    3. Zhou HX
    (2009) Fundamental aspects of protein-protein association kinetics. Chem Rev 109:839–860.
    OpenUrlCrossRefPubMed
  43. ↵
    1. Segel IH
    (1975) Simple inhibition systems, in Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems, pp 109, John Wiley & Sons, New York.
  44. ↵
    1. Shou M,
    2. Grogan J,
    3. Mancewicz JA,
    4. Krausz KW,
    5. Gonzalez FJ,
    6. Gelboin HV, and
    7. Korzekwa KR
    (1994) Activation of CYP3A4: evidence for the simultaneous binding of two substrates in a cytochrome P450 active site. Biochemistry 33:6450–6455.
    OpenUrlCrossRefPubMed
  45. ↵
    1. Smith BD,
    2. Sanders JL,
    3. Porubsky PR,
    4. Lushington GH,
    5. Stout CD, and
    6. Scott EE
    (2007) Structure of the human lung cytochrome P450 2A13. J Biol Chem 282:17306–17313.
    OpenUrlAbstract/FREE Full Text
  46. ↵
    1. Sohl CD,
    2. Isin EM,
    3. Eoff RL,
    4. Marsch GA,
    5. Stec DF, and
    6. Guengerich FP
    (2008) Cooperativity in oxidation reactions catalyzed by cytochrome P450 1A2: highly cooperative pyrene hydroxylation and multiphasic kinetics of ligand binding. J Biol Chem 283:7293–7308.
    OpenUrlAbstract/FREE Full Text
  47. ↵
    1. Ueng Y-F,
    2. Kuwabara T,
    3. Chun YJ, and
    4. Guengerich FP
    (1997) Cooperativity in oxidations catalyzed by cytochrome P450 3A4. Biochemistry 36:370–381.
    OpenUrlCrossRefPubMed
  48. ↵
    1. Wakayama N,
    2. Toshimoto K,
    3. Maeda K,
    4. Hotta S,
    5. Ishida T,
    6. Akiyama Y, and
    7. Sugiyama Y
    (2018) In silico prediction of major clearance pathways of drugs among 9 routes with two-step support vector machines. Pharm Res 35:197.
    OpenUrl
  49. ↵
    1. Walsh C
    (1979) Enzymatic Reaction Mechanisms, pp 67–71, W. H. Freeman, San Francisco, CA.
  50. ↵
    1. Wang A,
    2. Savas U,
    3. Stout CD, and
    4. Johnson EF
    (2011) Structural characterization of the complex between alpha-naphthoflavone and human cytochrome P450 1B1. J Biol Chem 286:5736–5743.
    OpenUrlAbstract/FREE Full Text
  51. ↵
    1. Wiebel FJ,
    2. Leutz JC,
    3. Diamond L, and
    4. Gelboin HV
    (1971) Aryl hydrocarbon (benzo(a)pyrene) hydroxylase in microsomes from rat tissues: differential inhibition and stimulation by benzoflavones and organic solvents. Arch Biochem Biophys 144:78–86.
    OpenUrlCrossRefPubMed
  52. ↵
    1. Wienkers LC and
    2. Heath TG
    (2005) Predicting in vivo drug interactions from in vitro drug discovery data. Nat Rev Drug Discov 4:825–833.
    OpenUrlCrossRefPubMed
  53. ↵
    1. Zang H,
    2. Fang Q,
    3. Pegg AE, and
    4. Guengerich FP
    (2005) Kinetic analysis of steps in the repair of damaged DNA by human O6-alkylguanine-DNA alkyltransferase. J Biol Chem 280:30873–30881.
    OpenUrlAbstract/FREE Full Text
  54. ↵
    1. Zhang D,
    2. Zhu M, and
    3. Humphreys WG
    (2008) Drug Metabolism in Drug Design and Development: Basic Concepts and Practice, Wiley, Hoboken, NJ.
Back to top

In this issue

Download PDF
Article Alerts
Email Article
Citation Tools

Research ArticleArticle

Enzyme Kinetic Models

F. Peter Guengerich
Drug Metabolism and Disposition November 1, 2019, 47 (11) 1232-1239; DOI: https://doi.org/10.1124/dmd.119.088732
Twitter logo Facebook logo Mendeley logo

Jump to section

Advertisement