Advertisement
Research ArticleArticle

Critical Impact of Drug-Drug Interactions via Intestinal CYP3A in the Risk Assessment of Weak Perpetrators Using Physiologically Based Pharmacokinetic Models

Makiko Yamada, Shin-ichi Inoue, Daisuke Sugiyama, Yumi Nishiya, Tomoko Ishizuka, Akiko Watanabe, Kengo Watanabe, Shinji Yamashita and Nobuaki Watanabe
Drug Metabolism and Disposition April 2020, 48 (4) 288-296; DOI: https://doi.org/10.1124/dmd.119.089599

Abstract

A great deal of effort has been being made to improve the accuracy of the prediction of drug-drug interactions (DDIs). In this study, we addressed CYP3A-mediated weak DDIs, in which a relatively high false prediction rate was pointed out. We selected 17 orally administered drugs that have been reported to alter area under the curve (AUC) of midazolam, a typical CYP3A substrate, 0.84–1.47 times. For weak CYP3A perpetrators, the predicted AUC ratio mainly depends on intestinal DDIs rather than hepatic DDIs because the drug concentration in the enterocytes is higher. Thus, DDI prediction using simulated concentration-time profiles in each segment of the digestive tract was made by physiologically based pharmacokinetic (PBPK) modeling software GastroPlus. Although mechanistic static models tend to overestimate the risk to ensure the safety of patients, some underestimation is reported about PBPK modeling. Our in vitro studies revealed that 16 out of 17 tested drugs exhibited time-dependent inhibition (TDI) of CYP3A, and the subsequent DDI simulation that ignored these TDIs provided false-negative results. This is considered to be the cause of past underestimation. Inclusion of the DDI parameters of all the known DDI mechanisms, reversible inhibition, TDI, and induction, which have opposite effects on midazolam AUC, to PBPK model was successful in improving predictability of the DDI without increasing false-negative prediction as trade-off. This comprehensive model-based analysis suggests the importance of the intestine in assessing weak DDIs via CYP3A and the usefulness of PBPK in predicting intestinal DDIs.

SIGNIFICANCE STATEMENT Although drug-drug interaction (DDI) prediction has been extensively performed previously, the accuracy of prediction for weak interactions via CYP3A has not been thoroughly investigated. In this study, we simulate DDIs considering drug concentration-time profile in the enterocytes and discuss the importance and the predictability of intestinal DDIs about weak CYP3A perpetrators.

Introduction

When the potential for drug-drug interactions (DDIs) is suggested by the results of in vitro studies during the development of a new drug, the magnitude of the in vivo DDIs is predicted using models, such as static models or physiologically based pharmacokinetic (PBPK) models, to determine the necessity of clinical studies (Food and Drug Administration, 2017). In general, an area under the curve ratio (AUCR) of a substrate with or without a perpetrator between 0.8 and 1.25 represents no DDIs. Many previous studies have focused on predicting strong interactions; however, it is important to predict weak interactions around the thresholds accurately because they influence strategies for drug development. Because the risk in clinical DDI studies is low but not zero for participants and the cost burden to the drug development process is passed on to the healthcare system, unnecessary studies should be avoided (Greenblatt, 2014). In our survey using PharmaPendium (Elsevier, Amsterdam, Netherlands), a data base of drug approval documents, among the compounds for which product labels include the results of clinical DDI studies with midazolam, approximately half of the labels stated that there was no interaction (Supplemental Data). These studies may not have been needed if the interaction could have been accurately predicted. Although a static model is useful to evaluate DDI risk, it assumes that theoretical maximum concentrations are sustained, which is not true in the in vivo environment and often leads to a false-positive prediction. Vieira et al. (2014) evaluated the predictability of a mechanistic static model using 119 clinical DDI study results with midazolam, a typical CYP3A substrate, and although the false-negative rate was low (2.3%), the false-positive rate was approximately 70%. A recent systematic study by Hsueh et al. (2018) concluded that PBPK models are useful in the determination of the necessity of clinical trials; however, the negative predictive error was approximately 50%. Although most false-negative cases involve weak inhibitors, their underestimation is undesirable.

For the prediction of weak interactions, the presence or absence of interaction often depends on intestinal interactions because the drug concentration in enterocytes is usually higher than in hepatocytes. To predict intestinal DDI more accurately, it is necessary to create a PBPK model that simulates an enterocyte concentration-time profile based on the behavior of a compound during absorption. When predicting the DDI of strong inhibitors, CYP3A in the intestine is maximally inhibited; therefore, the reciprocal of intestinal availability (Fg), 1/Fg, can be used as the magnitude of the DDI in the intestine (Galetin et al., 2007, 2008). Various studies focused on the predictability of strong DDIs, thus the accuracy of prediction for intestinal interactions has not been as thoroughly investigated as that for hepatic interactions.

Another important point is the use of appropriate in vitro DDI parameters. When we individually examined the models that exhibited false-negative predictions in past studies (Hsueh et al., 2018), we discovered that only inhibition constants for reversible inhibition (Ki) were calculated for some perpetrators, even though the potential of time-dependent inhibition (TDI) and induction was suggested in other studies (Zimmerlin et al., 2011; Vieira et al., 2014). For compounds that exhibit both reversible inhibition and TDI, ignoring TDI parameters may cause underestimation. In addition, the evaluation of the predictability of DDIs for compounds that exhibit both inhibition and induction is insufficient. Because of this, the DDI guidance recommends a conservative approach in which the inhibition and induction mechanisms are considered separately (Food and Drug Administration, 2017), and this leads to overestimation of the DDI risk.

In this study, calculations were conducted using virtual compounds with various CYP3A inhibitory activities by static models to show the importance of the intestine in DDI prediction. Subsequently, reversible inhibition, TDI, and the induction potential of CYP3A were evaluated by in vitro experiments to obtain data under identical conditions for weak perpetrators, wherein observed midazolam AUCR in a clinical DDI study was less than 2. The effects of reversible inhibition, TDI, and induction were simulated separately and concurrently by PBPK models using the DDI module in GastroPlus (ver. 9.6.0001; Simulation Plus, Lancaster, CA), which incorporated the Advanced Compartmental Absorption and Transit model enabling a physiologically relevant simulation of the concentration-time profiles in each segment of the digestive tract, and the accuracy of the prediction was evaluated.

Materials and Methods

Compounds and Reagents

Midazolam was purchased from Wako Pure Chemical Industries (Osaka, Japan). The metabolite of midazolam, 1′-hydroxymidazolam, was purchased from Sigma-Aldrich (St. Louis, MO). As an internal standard, 13C-1′-hydroxymidazolam was obtained from Corning (Corning, NY). The following marketed drugs were used for the evaluation of the potential to inhibit or induce CYP3A: atomoxetine hydrochloride (Tokyo Chemical Industry, Tokyo, Japan), atorvastatin (LKT Laboratories, St. Paul, MN), azithromycin dehydrate (LKT Laboratories), casopitant mesylate (Santa Cruz Biotechnology, Dallas, TX), cimetidine (Sigma-Aldrich), deferasirox (Toronto Research Chemicals, North York, Canada), ethinyl estradiol (Sigma-Aldrich), everolimus (Selleck Chemicals, Houston, TX), felodipine (Sigma-Aldrich), fluoxetine (Sigma-Aldrich), fluvoxamine (Sigma-Aldrich), pazopanib (ChemieTek, Indianapolis, IN), ranitidine hydrochloride (Sigma-Aldrich), roxithromycin (Sigma-Aldrich), simvastatin (Wako Pure Chemical), suvorexant (AdooQ-BioScience, Irvine, CA), and tadalafil (Selleck Chemicals). Pooled human microsomes (mixed sex, 20 mg protein/ml) and pooled cryopreserved human hepatocytes were purchased from Sekisui XenoTech, LLC (Kansas City, KS). NADPH Regeneration System Solution A and NADPH Regeneration System Solution B were purchased from Corning.

Clinical DDI Study Data Collection

The AUCR values for midazolam in the presence of CYP3A perpetrators in clinical DDI studies were collected from the Drug Interaction Database (https://www.druginteractioninfo.org/, University of Washington, Seattle, WA); in vitro DDI data were also collected from the Drug Interaction Database. Seventeen marketed drugs were chosen for the current study, in which the AUCR of midazolam was 0.8–2 in the clinical DDI study, and an inhibitory effect on CYP3A was observed in the in vitro study. A summary of the clinical studies used in the prediction is shown in Supplemental Table 1.

Determination of In Vitro Perpetrator Parameters for CYP3A

Inhibition.

The potential for reversible and time-dependent inhibition of the 17 marketed drugs (atomoxetine, azithromycin, atorvastatin, casopitant, cimetidine, deferasirox, ethinyl estradiol, everolimus, felodipine, fluoxetine, fluvoxamine, pazopanib, ranitidine, roxithromycin, simvastatin, suvorexant, and tadalafil) on CYP3A was investigated using pooled human liver microsomes. To reduce the effect of protein binding to microsomal proteins, relatively low protein concentrations (0.02 mg/ml for reversible inhibition and 0.2 mg/ml for TDI) were used. The activity of CYP3A was estimated from the assay of midazolam 1′-hydroxylation activity. The perpetrators were dissolved in acetonitrile or methanol, and midazolam was dissolved in methanol:water [1:1]; the final concentration of the solvent was less than 1.5%. Methanol and acetonitrile were chosen as the solvent instead of DMSO, which is frequently used to dissolve lipophilic compounds, because DMSO affects the TDI activity of some compounds, most likely via the inhibition of metabolism (Nishiya et al., 2010; Aasa et al., 2013). For reversible inhibition, the incubation mixtures containing human liver microsomes, potassium phosphate buffer, midazolam (2, 4, and 8 μM), and each perpetrator were prewarmed at 37°C for 5 minutes. Then incubation was initiated by the addition of the final concentrations of 5% for the NADPH Regeneration System Solution A and 1% for the NADPH Regeneration System Solution B (NADPHgs). After incubation at 37°C for 5 minutes, the reaction was terminated by mixing with a stop solution [acetonitrile:methanol (1:1) containing an internal standard]. To determine the inactivation parameters for TDI, the incubation mixture without midazolam was prewarmed at 37°C for 5 minutes, and the NADPHgs were added to initiate the incubation. Samples were taken immediately (at 0 minutes) and, at 15, 30, and 60 minutes after the start of incubation, diluted ten times with the incubation mixture containing NADPHgs and midazolam (40 μM), and then they were incubated for 5 minutes; subsequently, the reaction was terminated by mixing with the stop solution. The samples were centrifuged, and the concentrations of the midazolam metabolite, 1′-hydroxymidazolam, in each supernatant was measured using liquid chromatography-tandem mass spectrometry. More details of the method are shown in the Supplemental Method.

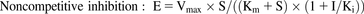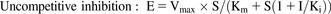The metabolic activity (picomoles per minute per milligram protein) of CYP3A was obtained by dividing the 1′-hydroxymidazolam concentration by microsomal protein concentration and incubation time and analyzed by eqs. 1–3 using Phoenix WinNonlin Ver. 6.3 (Certara, Princeton, NJ).Embedded Image(1)Embedded Image(2)Embedded Image(3)where E is the metabolic activity, Vmax is the maximum value of metabolic activity, S is the substrate concentration, Km is the Michaelis constant, and I is the concentration of the test compound. After consideration of Akaike’s information criterion, the most appropriate model was selected to determine Ki.

To calculate the inactivation parameters, the natural logarithm of the remaining activity at each drug concentration was plotted against the preincubation time. The apparent inactivation rate constant (kobs) was determined from the negative slope of the fitting line from the area showing an initial inhibition rate for each drug concentration. To determine the maximum inactivation rate constant (kinact) and the concentration at half kinact (KI) of the drug, the relationship between the kobs value and I was fitted into the eq. 4 using WinNonlin. When a decrease in kobs was observed at higher concentrations, the data were removed, and the parameters were calculated using the remaining data.Embedded Image(4).

Induction.

The potential of 13 marketed drugs (azithromycin, atomoxetine, cimetidine, casopitant, deferasirox, everolimus, felodipine, fluvoxamine, pazopanib, ranitidine, roxithromycin simvastatin, and tadalafil) to induce CYP3A4 was investigated using pooled cryopreserved human hepatocytes. For the remaining four compounds (atorvastatin, ethinyl estradiol, fluoxetine, and suvorexant), the values from the literature were available. Rifampicin (10 μM) and omeprazole (50 μM) were used as positive controls, and gatifloxacin (10 μM) was used as a negative control. The drugs were dissolved in DMSO and diluted 1000 times in modified Lanford medium (Nissui Pharmaceutical, Tokyo, Japan). The hepatocytes were seeded at 6 × 104 cells/well in 96-well culture plates and left to adhere overnight. On the day after, the incubation medium was replaced with the medium containing drugs, and the plate was cultured overnight. These steps were repeated, resulting in a total treatment time of 48 hours. All experiments were performed in triplicate. After the incubation, the RNA was extracted and analyzed by reverse transcription-polymerase chain reaction. Relative mRNA expression was calculated by dividing the quantity of CYP3A4 mRNA by the quantity of glyceraldehyde-3-phosphate dehydrogenase mRNA. A more detailed method is shown in the Supplemental Method.

The fold change in expression was calculated by dividing the mRNA expression of the drug by the mRNA expression of the same gene in the solvent-treated control sample. The induction parameters, the maximum induction effect (Emax) and half maximum effective concentration (EC50), were calculated using eq. 5 using Phoenix WinNonlin (ver. 6.3).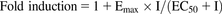Embedded Image(5).

Prediction Using Mechanistic Static Model

The AUCR of midazolam with and without the perpetrator was predicted using a mechanistic static model with eq. 6, in accordance with the draft guidance for DDI by the Food and Drug Administration (Food and Drug Administration, 2017).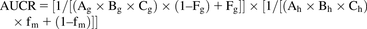Embedded Image(6).In eq. 6, Fg is the fraction available after intestinal metabolism, and fm is the fraction of systemic clearance (CL) of a substrate mediated by the enzyme that is subject to inhibition/induction; subscripts “h” and “g” denote the liver and gut, respectively. The Fg of midazolam was calculated to be 0.54 based on the absolute bioavailability (0.30) and hepatic availability (0.56) from literature (Thummel et al., 1996), assuming the fraction absorbed (Fa) was 1. The fm of midazolam was set to 0.93 (Zhou and Zhou, 2009). Although Fg and fm change depending on the dose of midazolam, constant values were used for the static model analysis. Terms A, B, and C represent reversible inhibition, TDI, and induction, respectively, and were calculated from the following eqs. 7–9:Embedded Image(7)Embedded Image(8)Embedded Image(9)where kdeg is the apparent first-order degradation rate constant of CYP3A, and 0.0005 minute−1 was used both for gut and liver (Zhang et al., 2009), which is the same value used in GastroPlus ver. 9.6.0001; d is calibration factor, and 1 was used.

To calculate the concentration of perpetrator in intestine ([I]g), eq. 10 (Rostami-Hodjegan and Tucker, 2004) was used as recommended in the DDI guidance by the Food and Drug Administration.Embedded Image(10)where ka is the first-order absorption rate constant, and Qen is the blood flow through enterocytes (18 L/h) (Yang et al., 2007).

When the DDI of the marketed drugs was predicted, Fa used in the static model was the same as that calculated by GastroPlus (Supplemental Table 3) to allow comparison with the result of the analysis. Because GastroPlus calculates time-dependent ka instead of single ka, the ka for the static model analysis was calculated from the concentration-time profile of each drug from the literature using Phoenix WinNonlin (Supplemental Table 3). The unbound fraction in plasma (fu,p) was adjusted by GastroPlus for possible binding to plasma lipids (fu,p,adj, Supplemental Table 4). For the calculation of steady-state plasma concentration (Css), AUCinf at a single dose was simulated with GastroPlus and used. Most of the in vitro DDI parameters used were obtained in the current study; the induction data of atorvastatin (Vieira et al., 2014), ethinyl estradiol (Fahmi et al., 2008), fluoxetine (Fahmi et al., 2008), and suvorexant (Prueksaritanont et al., 2013) were obtained from the literature. Ki, KI, and EC50 were corrected to the unbound value using the in vitro unbound fraction (fu,inc), predicted by GastroPlus (Supplemental Table 4). When fu,inc was calculated for the microsomes and hepatocytes, Calc (Hallifax)-HLM (Hallifax and Houston, 2006) and Calc (Austin)-Hep (Austin et al., 2005) in GastroPlus were used, respectively.

Static Model Analysis of Virtual Compounds

To show the importance of the interaction in the intestine, the AUCR of virtual compounds with various Ki values (from 0.2 to 100 μM) was calculated using a mechanistic static model. The properties of the virtual compound were as follows: mol. wt., 500; Fa, 1; ka, 1 hour−1; CL, 20 L/h; and fu,p, 0.1. For the concentration of the perpetrator in the liver ([I]h), the unbound Css was calculated by dividing the AUC by dosing interval, and AUC was calculated by dividing the dose by CL. The AUCR based on CYP3A inhibition in the intestine, liver, and both the intestine and liver were calculated at a daily dose of 100 mg. In addition, the AUCR was calculated with fixed Ki (1 μM) and various doses (1–500 mg).

Prediction Using PBPK Model

GastroPlus version 9.6.0001 was used to construct the human PBPK model. The Advanced Compartmental Absorption and Transit model, compartmental PK model, and DDI module in GastroPlus were used to simulate intestinal absorption and metabolism, systemic distribution and elimination, and DDI, respectively. For parameters that are not specifically described below, the values incorporated into, or predicted by, GastroPlus were used (e.g., human physiologic parameters).

Substrate (Midazolam) Model.

The parameters used for the midazolam model are shown in Table 1. The effective permeability (Peff), octanol-water partition coefficient (logP), blood-to-plasma concentration ratio, fu,p, and solubility data were obtained from the literature (Andersin, 1991; Gertz et al., 2011). The fu,p was adjusted by GastroPlus for possible binding to plasma lipids. The distribution parameters, the central compartment volume (Vc), rate constant for the distribution of the drug to the second compartment (K12), and rate constant for the distribution of the drug from the second compartment (K21), were determined using the PKPlus module in GastroPlus to fit the plasma concentration-time profile after intravenous and oral administration of midazolam (Thummel et al., 1996). The in vitro kinetic parameters of midazolam metabolism by CYP3A [i.e., Km and Vmax] were obtained from literature (Thummel et al., 1996), and then Vmax was converted to in vivo values using microsomal protein concentration (38 mg/g liver) and liver weight (1800 g), the default values in GastroPlus ver. 9.6. To predict intestinal metabolism, GastroPlus uses the enzyme-kinetic parameters generated from human liver microsomes based on the abundance ratio of the enzyme (Agoram et al., 2001). The intrinsic clearance values obtained from human liver microsomes and human intestinal microsomes are not significantly different after normalization for tissue-specific CYP3A abundance (Gertz et al., 2010), and the prediction error of Fg by GastroPlus is less than 2-fold (Heikkinen et al., 2012). In the current study, about 2-fold underestimation of midazolam Fg was observed when the same Vmax for liver and intestine was used; therefore, the Vmax for intestinal CYP3A was reduced by approximately half to achieve the observed Fg (0.54). The use of a different Vmax for the liver and intestine was not originally intended, but it was essential to improve the accuracy of the prediction.

View this table:
TABLE 1

Physicochemical and pharmacokinetic parameters of midazolam used for simulation

Perpetrator Model.

The solubility, Peff, logP, and fu,p of the 17 marketed drugs were collected to construct the perpetrator models (Supplemental Tables 4–6). These data were collected from data bases (PubChem, https://pubchem.ncbi.nlm.nih.gov/; and the Drug Interaction Database, https://www.druginteractioninfo.org/, University of Washington), determined in in-house studies, obtained from literature, or predicted from the compound structure by the ADMET Predictor incorporated in GastroPlus. When the solubility in water was known, and the pH of the aqueous solution was unknown, the pH of the saturated solution was predicted using GastroPlus. The bile salt influence on in vivo solubility (solubilization ratio) was calculated from the biorelevant solubility predicted by GastroPlus (Supplemental Table 5). The solubility versus pH profiles were calculated from the solubility at reference pH and pKa (Supplemental Table 5) by GastroPlus. For seven drugs, the predicted dissolution rate did not appear to be appropriate, thus the particle size was decreased from the default radius of 25 µm to fit the observed concentration-time profile. Although it may be necessary to change the precipitation time in some cases, the default value (900 seconds) was used for all compounds in this study. The PK parameters, such as CL, Vc, K12, and K21, were optimized to fit the concentration-time profiles after oral administration obtained from literature (Supplemental Table 7). Although it is desirable to fit the profiles after intravenous administration, they were unavailable for most compounds. For compounds with known large first-pass effects (FPEs), FPE was calculated and input into GastroPlus models using bioavailability, CL (assumed to be equal to hepatic clearance), Fg, and hepatic blood flow, obtained from the literature and from a data base, assuming that Fa was 1. The calculated FPE is shown in Supplemental Table 7. For the gut physiology model, “Human-Physiological-Fasted” or “Human-Physiological-Fed,” as incorporated in the software, was used depending on the food condition of the source clinical studies. The absorption scaling factor was calculated by Opt logD Model SA/V 6.1 incorporated in the software. The unbound fraction in enterocytes was set to 100% (default value).

DDI Simulation.

DDI simulation for midazolam and each perpetrator was conducted using the dynamic simulation in the DDI module of GastroPlus. The dosing information of substrate and perpetrators is summarized in Supplemental Table 1. The simulation used four different settings: 1) reversible inhibition parameter only, 2) both reversible inhibition and TDI parameters, 3) induction parameter only, and 4) all parameters available, to compare the effect of each mechanism. The AUCRs based on the interactions in the gut and liver were calculated separately [AUCR based on intestinal DDI (AUCRg) and AUCR based on hepatic DDI (AUCRh), respectively].

Evaluation of Predictive Performance

The traditional approach to evaluate the predictive performance based on whether predictions fall within a 2-fold range of the observed data is not suitable for weak perpetrators. For example, when actual AUC ratio is 1.5 (weak inhibitor), the acceptance range is from 0.75 (inducer) to 3 (moderate inhibitor). Therefore, the success rate of the prediction was calculated using the method proposed by Guest et al. (2011) using eqs. 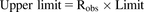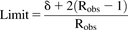11–13.Embedded Image(11)Embedded Image(12)Embedded Image(13)where Robs is observed AUCR or reciprocal of observed AUCR for inhibitor (AUCR > 1) or inducer (AUCR < 1), respectively, and δ is a parameter that accounts for variability. When δ = 1, there is no variability, and when δ = 1.25 (used in this study) and Robs = 1, then the limits on AUCR are between 0.80 and 1.25, corresponding to the conventional 20% limits used in bioequivalence testing.

Results

Static Model Analysis of Virtual Compounds.

To show the contribution of liver and intestine, the AUCR of midazolam was calculated by static models with Ki value ranging from 0.2 to 100 μM and fixed-dose (100 mg) or a fixed Ki (1 μM) and dose ranging from 1 to 500 mg. The results are shown in Fig. 1, respectively. According to the properties of the virtual compounds written in the method, the [I]g and [I]h of the virtual compounds were 11.1 and 0.416 μM at 100 mg of dose, respectively. When the inhibition was weak (i.e., Ki was large, or dose was small), the AUCR caused by the interaction in the intestine was larger than that in the liver. When the inhibition is strong, the DDI in the intestine is saturated to 1/Fg (AUCR: 1.85), and the effect in the liver is larger.

Fig. 1.
Fig. 1.

The relationship between the AUCR of midazolam and Ki with fixed dose [100 mg, (A)] or doses with fixed Ki [1 μM, (B)] in static model analysis using virtual compounds.

In Vitro DDI Study.

The parameters for reversible inhibition and TDI are summarized in Table 2, and the kinetic plots are shown in Supplemental Figs. 1 and 2, respectively. Among the 17 tested marketed drugs (atomoxetine, azithromycin, atorvastatin, casopitant, cimetidine, deferasirox, ethinyl estradiol, everolimus, felodipine, fluoxetine, fluvoxamine, pazopanib, ranitidine, roxithromycin, simvastatin, suvorexant, and tadalafil), 16 drugs (all drugs except azithromycin) showed reversible inhibition, and Ki was calculated (Table 2). The reversible inhibition of azithromycin was very weak, and Ki was above the maximum concentration of the inhibitor tested (>1000 μM). Ethinyl estradiol and tadalafil were considered to be noncompetitive inhibitors by the analysis of Akaike’s information criterion, and the other 14 drugs were considered to be competitive inhibitors. The obtained Ki values of most compounds were comparable to those already reported in the literature (Supplemental Table 2). Among the 17 tested marketed drugs, 16 drugs showed TDI, and KI and kinact were calculated (Table 2). Atomoxetine did not show TDI. When the obtained KI and kinact were compared with the values from the literature, a large difference was observed for some compounds, presumably because of the difference in the experimental conditions (Supplemental Table 2), and the difference in kinact/KI between the values in this study and from the literature was smaller than that of each KI and kinact. Among the 13 marketed drugs tested for induction, seven drugs (casopitant, everolimus, felodipine, fluvoxamine, pazopanib, simvastatin, and tadalafil) had an inductive effect, and EC50 and Emax were calculated (Supplemental Fig. 3; Table 2). For the remaining six drugs (atomoxetine, azithromycin, cimetidine, deferasirox, ranitidine, and roxithromycin), the maximum fold induction was less than 2-fold. The fold induction of positive controls was 15.5–24.5 and 5.42–12.7 for rifampicin and omeprazole, respectively. No induction was observed by the negative control gatifloxacin.

View this table:
TABLE 2

In vitro inhibition and induction parameters used for the simulation

DDI Prediction Using GastroPlus.

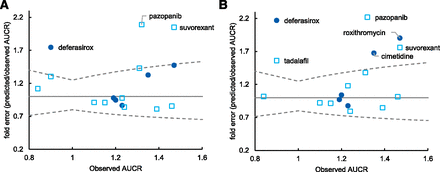
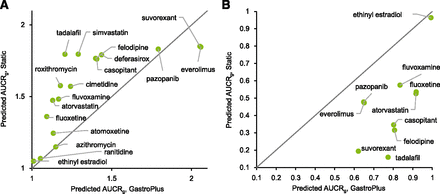
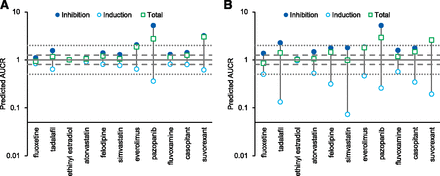
DDI simulation was conducted using the dynamic simulation in the DDI module. The dosing regimens used for the simulation were the same as for the clinical studies. These are summarized in Supplemental Table 1. The plots of observed versus predicted AUCR by GastroPlus using the reversible inhibition parameter only and both reversible inhibition and TDI parameters, respectively, are shown Fig. 2. Of the seven drugs that showed positive DDIs in clinical studies, five were predicted as negative (false-negative) when only Ki was incorporated (Fig. 2A). When TDI parameters were also incorporated, all seven compounds were predicted as positive, although 4 out of the 10 compounds with observed negative DDIs were also predicted as positive; that is, they were false positives (Fig. 2B). The relationship of AUCR of midazolam observed in the clinical studies and predicted by GastroPlus with all in vitro DDI parameters (reversible inhibition, time-dependent inhibition, and induction) incorporated is shown in Table 3. The predictive performance was evaluated using the approach proposed by Guest et al. (2011) and compared with the results by static models, as shown in Fig. 3. The y-axis of the graphs is shown as fold error (predicted/observe). The success rate was calculated as 76% and 65% for GastroPlus and static model, respectively. An overestimation was observed in some drugs; however, there was no underestimation. The calculated AUCRg and AUCRh were also shown in Table 3. For most compounds, the AUCRh was approximately 1, and AUCRg showed a larger contribution to the change of AUCR. The relationship between AUCRg simulated by GastroPlus and the static model when inhibitory (both reversible and time-dependent) and inducing effects were simulated separately is shown in Fig. 4. For inhibition (Fig. 4A), ethinyl estradiol, ranitidine, and azithromycin showed similarly small AUCRg, and pazopanib showed similarly large AUCRg in the GastroPlus and static model; everolimus and suvorexant showed larger AUCRg in GastroPlus. For other compounds, the prediction of inhibition tended to be stronger by the static model than by GastroPlus. For induction (Fig. 4B), smaller AUCRg (i.e., stronger interaction) was predicted by the static model than by GastroPlus, except for with ethinyl estradiol, for which the interaction was very weak. The relationship of predicted AUCR using inhibition, induction, and both inhibition and induction is shown in Fig. 5. Incorporation of both inhibition and induction mechanisms resulted in offset; the decrease in metabolic activity due to inhibition was alleviated by the increase in enzymes due to induction.

Fig. 2.
Fig. 2.

Observed vs. predicted AUCR of midazolam by GastroPlus dynamic simulation using reversible inhibition only (A) and reversible and time-dependent inhibition (B). The dashed line represents 1.25-fold AUCR. FN, false negative; FP, false positive; TN, true negative; TP, true positive.

View this table:
TABLE 3

Summary of predicted AUCR of midazolam by GastroPlus dynamic simulation incorporating all relevant mechanisms based on in vitro data (reversible inhibition, time-dependent inhibition, and induction as applicable)

Fig. 3.
Fig. 3.

Fold error of predicted midazolam AUCR via CYP3A inhibition or both inhibition and induction by GastroPlus. The closed circles represent the compounds for which only inhibitory effects were observed, and the open squares represent the compounds with both inhibition and induction in vitro. The solid line represents the line of unity, and the dashed lines represent the upper and lower limits of the success of the prediction.

Fig. 4.
Fig. 4.

The comparison of the predicted AUCR of midazolam via intestinal CYP3A inhibition (A) and induction (B) using GastroPlus and the static model. The solid line represents the line of unity.

Fig. 5.
Fig. 5.

The offset of inhibition and induction by GastroPlus (A) and the static model (B) for perpetrators exhibiting both inhibition and induction of CYP3A. The solid line, dashed lines, and dotted lines represent 1-, 1.25- or 0.8-, and 2- or 0.5-fold AUCR, respectively. The seven compounds from the left were compounds with no interaction in the clinical studies.

Discussion

To judge the necessity of a clinical DDI study, the accuracy of the prediction of weak DDIs is important, and when predicting the DDI of weak inhibitors, intestinal effects are considered significant. To help imaging, the relationship between DDI in the gut and liver (Fig. 1) was prepared using virtual compounds. The left end of Fig. 1, wherein inhibition is weak, intestinal CYP3A is not completely inhibited, and liver interactions are hardly observed, suggesting the importance of intestine when discussing weak DDI. Midazolam is often used as a CYP3A probe substrate, and many clinical DDI study data are available. DDI prediction of midazolam has been extensively performed previously, but many focused on strong interactions, and to assess the predictability of DDIs via intestinal CYP3A, weak DDIs should be the focus. Therefore, 17 weak perpetrators, for which observed midazolam AUCR in a clinical DDI study was less than 2, were selected to evaluate predictability by GastroPlus. At first we tried to predict in vivo DDI using in vitro values from the literature; however, there were several problems. For some compounds, a huge variation of the parameters was observed in the literature; microsomal protein concentration, which is necessary to calculate fu,inc, was unknown; and positive TDI or induction was reported without calculated parameters. Thus, we conducted in vitro studies to obtain the data under the same experimental conditions.

When the AUCRs of midazolam predicted by GastroPlus were compared with the observed values, the success rate was 76% by evaluation using the strict criteria for weak perpetrators proposed by Guest et al. (2011), indicating the utility of PBPK modeling approach. Only 3 out of 17 compounds clearly missed the criteria, all of which were overestimated. The absence of underestimation is very important, as models with frequent underestimation cannot be used to determine the necessity of clinical DDI studies. Among the compounds with poor predicted result, overestimation is reported about pazopanib and midazolam DDI when using TDI parameters from microsomes, and the prediction is improved by using the parameters from hepatocytes (Mao et al., 2016). The reason is not fully understood, but the involvement of plasma membranes and transporters on them has been pointed out. Thus, the cause of the overestimation in this study may be an in vitro system rather than a modeling. In addition, strong interactions of more than 2-fold and less than 0.5-fold were predicted when inhibition and induction of pazopanib were assessed separately (Fig. 5). These results may indicate the difficulty to predict the offset between strong inhibition and strong induction. Previous PBPK modeling analyses report an underestimation of weak perpetrators (Hsueh et al., 2018). However, in our study, no underestimation was observed when TDI was incorporated (Fig. 2B). Although TDIs are often considered as negative when there are no differences in IC50 with or without preincubation, some compounds that have been reported exhibiting no IC50 shifts (Haarhoff et al., 2017) showed positive TDI in our study (e.g., cimetidine, felodipine, and fluvoxamine). Sometimes preincubation results in the metabolism of the inhibitor, thereby reversible inhibition is reduced time-dependently and TDI is concealed. The absence of TDI should be determined with caution, since many compounds show the potential in screening studies (Zimmerlin et al., 2011). Thus, neglect of TDIs may contribute to the past underestimation, and it is not the problem of PBPK modeling approach itself.

Our models have some limitations. The physicochemical parameters, such as solubility, Peff, and logP (or logD), have critical effects on the predicted Fa and enterocyte concentration, thus the use of experimental value is desirable. However, predicted values by ADMET Predictor were used when experimental values were not available. It is desirable to determine PK parameters after absorption, such as CL, Vc, K12, and K21, using plasma concentration-time profiles after intravenous administration. However, they are often unavailable in the early stages of drug development, thus we optimized the PK parameters of perpetrators (Supplemental Table 7) by fitting the data after oral administration (Supplemental Fig. 4). The efflux transporters like P-glycoprotein and breast cancer resistance protein lower the levels of the substrate in epithelial cells. Several perpetrator drugs have been reported to be substrates for these transporters; however, the facts were not included in the predictions in this study. Despite such limitations, a success rate of the predicted AUCR by GastroPlus was 76%, which suggested that this method is sufficiently useful in the prediction of the DDI risk of weak perpetrators. For some perpetrators with known large FPEs, the FPE calculated from the literature PK parameters was entered. The ability to consider the metabolism of perpetrator drugs in the intestine and liver is one advantage of PBPK models over static models.

When DDIs of inhibition and induction were simulated separately, and the intestinal AUCR with GastroPlus and the static model was compared, the static models tended to predict the interaction more strongly than GastroPlus. This appeared reasonable, given that the static models assumed that the highest concentrations would persist for a long time. However, when the enterocyte concentrations calculated by GastroPlus were compared with [I]g, the maximum concentration was higher than [I]g, except for the compounds for which the FPE was entered. As an example, the relationship of simulated concentrations of the jejunum compartment 1 and [I]g is shown in Supplemental Fig. 5. It was suggested that the reason for the higher AUCRg was not always a higher concentration, and the duration of exposure was important. The reason for the difference in concentration is considered to be because [I]g was calculated assuming that the rates of drug influx into and efflux from epithelial cells were equal, whereas in GastroPlus influx is faster than efflux at the beginning of absorption. The difference in the Fg of midazolam is considered to be another reason for the higher AUCRg in the static models. Although Fg is constant in the static model, it is calculated by GastroPlus as small at low midazolam doses and large at high doses because GastroPlus includes saturable metabolism mechanism (Agoram et al., 2001). When simulating clinical studies with high midazolam doses (e.g., 15 mg), the AUCR was small even when the maximum inhibition of intestinal CYP3A was calculated because Fg without inhibition was close to 1. Such compounds may cause stronger interactions with lower doses of midazolam or other compounds with smaller Fg. In regard to the predictability of hepatic DDI, the correlation of AUCRh between the GastroPlus and static models was strong when an unbound Css was used for [I]h (Supplemental Fig. 6). The maximum unbound plasma concentration at the inlet to the liver, which was recommended for [I]h by DDI guidance for conservative prediction, was higher than the maximum concentration in the liver predicted by GastroPlus for most compounds (Supplemental Fig. 7). The use of unbound plasma concentration at the inlet to the liver in calculations contributed to the overestimation of static models.

When both inhibition and induction were considered simultaneously, the offset of the effects was observed (Fig. 5). The DDI guidance recommends a conservative approach in which the inhibition and induction effects are assessed separately (Food and Drug Administration, 2017) because the prediction of the offset of inhibition and induction is difficult. Although the offset of strong inhibitory and inducing effects can cause false-negative predictions, no significant underestimation was observed in our study. Therefore, when predicted inhibition and induction were weak (AUCR <2 and >0.5, respectively), the values after offset could be used to avoid clinical DDI studies. We did not include strong perpetrators in this study, thus the offsets of strong inhibition and induction should be evaluated in the future. Static models also showed relatively good predictability (Fig. 3B); however, there are some compounds with predicted strong inhibition and induction, and in these cases, it is difficult to judge whether clinical studies are not necessary (Fig. 5B). The balance between inhibition and induction varies with the timing of the administration of a perpetrator and a substrate. In this study, the same timing was used as in the referred clinical study, and in some studies, midazolam was administered 0.5–2 hours later than the perpetrator (Supplemental Table 1). The offset of TDI and induction was less affected by the timing of administration; however, in the offset of reversible inhibition and induction, inhibition was predicted to be weak by the delayed administration of midazolam (unpublished data). Therefore, PBPK models should be used for not only discussing the necessity of clinical studies but also the design.

In conclusion, our study demonstrates the importance of intestinal DDIs when assessing weak DDIs via CYP3A. It indicates that PBPK models are able to reasonably predict weak DDIs via intestinal CYP3A without underestimation by incorporating all of the mechanisms, including reversible inhibition, TDI, and induction. PBPK model can be used to judge the necessity of clinical DDI studies for CYP3A perpetrators, even with both inhibition and induction, and to avoid unnecessary clinical trials that burden subjects, ensuring the safety of patients.

Acknowledgments

The authors thank Daiichi Sankyo R.D. Novare for supporting the studies of in vitro physicochemical properties of perpetrator drugs and Sekisui Medical for supporting the CYP3A4 induction study. The authors also thank Dr. Michael Bolger and Dr. Viera Lukacova (Simulations Plus) and Professor Kiyomi Ito (Musashino University) for their expert advice.

Authorship Contributions

Participated in research design: Yamada, Inoue, Sugiyama, Nishiya, Ishizuka, A. Watanabe.

Conducted experiments: Yamada.

Performed data analysis: Yamada, Sugiyama, Nishiya.

Wrote or contributed to the writing of the manuscript: Yamada, Inoue, Sugiyama, Nishiya, Ishizuka, A. Watanabe, K. Watanabe, Yamashita, N. Watanabe.

Footnotes

Abbreviations

AUC
area under the curve
AUCR
AUC ratio
AUCRg
AUCR based on intestinal DDI
AUCRh
AUCR based on hepatic DDI
CL
systemic clearance
Css
steady-state plasma concentration
DDI
drug-drug interaction EC50 half maximum effective concentration
Emax
maximum induction effect
Fa
fraction absorbed
Fg
intestinal availability
FPE
first-pass effect
fm
fraction of CL of a substrate mediated by the enzyme that is subject to inhibition/induction
fu,inc
in vitro unbound fraction fu,p unbound fraction in plasma
[I]g
concentration of perpetrator in intestine for static model
K12
rate constant for the distribution of the drug to the second compartment
K21
rate constant for the distribution of the drug from the second compartment
ka
first-order absorption rate constant
Ki
reversible inhibition
KI
concentration at half kinact
kinact
inactivation rate constant
Km
Michaelis-Menten constant
kobs
apparent inactivation rate constant
NADPHgs
NADPH Regeneration System
PBPK
physiologically based PK
PK
pharmokinetic
TDI
time-dependent inhibition
Vc
central compartment volume
Vmax
maximum value of metabolic activity

References

  1. ↵
    1. Aasa J,
    2. Hu Y,
    3. Eklund G,
    4. Lindgren A,
    5. Baranczewski P,
    6. Malmquist J,
    7. Turek D, and
    8. Bueters T
    (2013) Effect of solvents on the time-dependent inhibition of CYP3A4 and the biotransformation of AZD3839 in human liver microsomes and hepatocytes. Drug Metab Dispos 41:159–169.
    OpenUrlAbstract/FREE Full Text
  2. ↵
    1. Agoram B,
    2. Woltosz WS, and
    3. Bolger MB
    (2001) Predicting the impact of physiological and biochemical processes on oral drug bioavailability. Adv Drug Deliv Rev 50 (Suppl 1):S41–S67.
    OpenUrlCrossRefPubMed
  3. ↵
    1. Andersin R
    (1991) Solubility and acid-base behaviour of midazolam in media of different pH, studied by ultraviolet spectrophotometry with multicomponent software. J Pharm Biomed Anal 9:451–455.
    OpenUrlCrossRefPubMed
  4. ↵
    1. Austin RP,
    2. Barton P,
    3. Mohmed S, and
    4. Riley RJ
    (2005) The binding of drugs to hepatocytes and its relationship to physicochemical properties. Drug Metab Dispos 33:419–425.
    OpenUrlAbstract/FREE Full Text
  5. ↵
    1. Fahmi OA,
    2. Maurer TS,
    3. Kish M,
    4. Cardenas E,
    5. Boldt S, and
    6. Nettleton D
    (2008) A combined model for predicting CYP3A4 clinical net drug-drug interaction based on CYP3A4 inhibition, inactivation, and induction determined in vitro. Drug Metab Dispos 36:1698–1708.
    OpenUrlAbstract/FREE Full Text
  6. ↵
    1. Food and Drug Administration
    (2017) Guidance for industry: in vitro metabolism- and transporter- mediated drug-drug interaction studies (draft guidance), US Department of Health and Human Services Center for Drug Evaluation and Research, FDA, Silver Spring, MD.
  7. ↵
    1. Galetin A,
    2. Gertz M, and
    3. Houston JB
    (2008) Potential role of intestinal first-pass metabolism in the prediction of drug-drug interactions. Expert Opin Drug Metab Toxicol 4:909–922.
    OpenUrlCrossRefPubMed
  8. ↵
    1. Galetin A,
    2. Hinton LK,
    3. Burt H,
    4. Obach RS, and
    5. Houston JB
    (2007) Maximal inhibition of intestinal first-pass metabolism as a pragmatic indicator of intestinal contribution to the drug-drug interactions for CYP3A4 cleared drugs. Curr Drug Metab 8:685–693.
    OpenUrlCrossRefPubMed
  9. ↵
    1. Gertz M,
    2. Harrison A,
    3. Houston JB, and
    4. Galetin A
    (2010) Prediction of human intestinal first-pass metabolism of 25 CYP3A substrates from in vitro clearance and permeability data. Drug Metab Dispos 38:1147–1158.
    OpenUrlAbstract/FREE Full Text
  10. ↵
    1. Gertz M,
    2. Houston JB, and
    3. Galetin A
    (2011) Physiologically based pharmacokinetic modeling of intestinal first-pass metabolism of CYP3A substrates with high intestinal extraction. Drug Metab Dispos 39:1633–1642.
    OpenUrlAbstract/FREE Full Text
  11. ↵
    1. Greenblatt DJ
    (2014) In vitro prediction of clinical drug interactions with CYP3A substrates: we are not there yet. Clin Pharmacol Ther 95:133–135.
    OpenUrl
  12. ↵
    1. Guest EJ,
    2. Aarons L,
    3. Houston JB,
    4. Rostami-Hodjegan A, and
    5. Galetin A
    (2011) Critique of the two-fold measure of prediction success for ratios: application for the assessment of drug-drug interactions. Drug Metab Dispos 39:170–173.
    OpenUrlAbstract/FREE Full Text
  13. ↵
    1. Haarhoff ZE,
    2. Kramer MA,
    3. Zvyaga TA,
    4. Zhang J,
    5. Bhutani P,
    6. Subramanian M, and
    7. Rodrigues AD
    (2017) Comprehensive evaluation of liver microsomal cytochrome P450 3A (CYP3A) inhibition: comparison of cynomolgus monkey and human. Xenobiotica 47:470–478.
    OpenUrl
  14. ↵
    1. Hallifax D and
    2. Houston JB
    (2006) Binding of drugs to hepatic microsomes: comment and assessment of current prediction methodology with recommendation for improvement. Drug Metab Dispos 34:724–726, author reply 727.
    OpenUrlFREE Full Text
  15. ↵
    1. Heikkinen AT,
    2. Baneyx G,
    3. Caruso A, and
    4. Parrott N
    (2012) Application of PBPK modeling to predict human intestinal metabolism of CYP3A substrates - an evaluation and case study using GastroPlus. Eur J Pharm Sci 47:375–386.
    OpenUrlCrossRefPubMed
  16. ↵
    1. Hsueh C-H,
    2. Hsu V,
    3. Pan Y, and
    4. Zhao P
    (2018) Predictive performance of physiologically-based pharmacokinetic models in predicting drug-drug interactions involving enzyme modulation. Clin Pharmacokinet 57:1337–1346.
    OpenUrl
  17. ↵
    1. Mao J,
    2. Tay S,
    3. Khojasteh CS,
    4. Chen Y,
    5. Hop CE, and
    6. Kenny JR
    (2016) Evaluation of time dependent inhibition assays for marketed oncology drugs: comparison of human hepatocytes and liver microsomes in the presence and absence of human plasma. Pharm Res 33:1204–1219.
    OpenUrlCrossRefPubMed
  18. ↵
    1. Nishiya Y,
    2. Nakamura K,
    3. Okudaira N,
    4. Abe K,
    5. Kobayashi N, and
    6. Okazaki O
    (2010) Effects of organic solvents on the time-dependent inhibition of CYP3A4 by diazepam. Xenobiotica 40:1–8.
    OpenUrlCrossRefPubMed
  19. ↵
    1. Prueksaritanont T,
    2. Chu X,
    3. Gibson C,
    4. Cui D,
    5. Yee KL,
    6. Ballard J,
    7. Cabalu T, and
    8. Hochman J
    (2013) Drug-drug interaction studies: regulatory guidance and an industry perspective. AAPS J 15:629–645.
    OpenUrlCrossRefPubMed
  20. ↵
    1. Rostami-Hodjegan A and
    2. Tucker G
    (2004) ‘In silico’ simulations to assess the ‘in vivo’ consequences of ‘in vitro’ metabolic drug-drug interactions. Drug Discov Today Technol 1:441–448.
    OpenUrlPubMed
  21. ↵
    1. Thummel KE,
    2. O’Shea D,
    3. Paine MF,
    4. Shen DD,
    5. Kunze KL,
    6. Perkins JD, and
    7. Wilkinson GR
    (1996) Oral first-pass elimination of midazolam involves both gastrointestinal and hepatic CYP3A-mediated metabolism. Clin Pharmacol Ther 59:491–502.
    OpenUrlCrossRefPubMed
  22. ↵
    1. Vieira ML,
    2. Kirby B,
    3. Ragueneau-Majlessi I,
    4. Galetin A,
    5. Chien JY,
    6. Einolf HJ,
    7. Fahmi OA,
    8. Fischer V,
    9. Fretland A,
    10. Grime K, et al.
    (2014) Evaluation of various static in vitro-in vivo extrapolation models for risk assessment of the CYP3A inhibition potential of an investigational drug. Clin Pharmacol Ther 95:189–198.
    OpenUrlCrossRefPubMed
  23. ↵
    1. Yang J,
    2. Jamei M,
    3. Yeo KR,
    4. Tucker GT, and
    5. Rostami-Hodjegan A
    (2007) Prediction of intestinal first-pass drug metabolism. Curr Drug Metab 8:676–684.
    OpenUrlCrossRefPubMed
  24. ↵
    1. Zhang X,
    2. Quinney SK,
    3. Gorski JC,
    4. Jones DR, and
    5. Hall SD
    (2009) Semiphysiologically based pharmacokinetic models for the inhibition of midazolam clearance by diltiazem and its major metabolite. Drug Metab Dispos 37:1587–1597.
    OpenUrlAbstract/FREE Full Text
  25. ↵
    1. Zhou ZW and
    2. Zhou SF
    (2009) Application of mechanism-based CYP inhibition for predicting drug-drug interactions. Expert Opin Drug Metab Toxicol 5:579–605.
    OpenUrlCrossRefPubMed
  26. ↵
    1. Zimmerlin A,
    2. Trunzer M, and
    3. Faller B
    (2011) CYP3A time-dependent inhibition risk assessment validated with 400 reference drugs. Drug Metab Dispos 39:1039–1046.
    OpenUrlAbstract/FREE Full Text
Back to top

In this issue

Download PDF
Article Alerts
Email Article
Citation Tools

Research ArticleArticle

PBPK Modeling of Weak Perpetrators via Intestinal CYP3A

Makiko Yamada, Shin-ichi Inoue, Daisuke Sugiyama, Yumi Nishiya, Tomoko Ishizuka, Akiko Watanabe, Kengo Watanabe, Shinji Yamashita and Nobuaki Watanabe
Drug Metabolism and Disposition April 1, 2020, 48 (4) 288-296; DOI: https://doi.org/10.1124/dmd.119.089599
Twitter logo Facebook logo Mendeley logo

Jump to section

Advertisement