Abstract
The use of multiple depletion curves for the estimation of maximum velocity of the metabolic reaction (Vmax), the Michaelis constant (Km), and intrinsic clearance (CLint) was thoroughly evaluated by means of experimental data and through a series of Monte Carlo simulations. The enzyme kinetics of seven compounds were determined using the multiple depletion curves method (MDCM), the traditional initial formation rate of metabolite method (IFRMM), and the “in vitro t½” method, and the parameter estimates that were derived from the three methods were compared. The impact of a change in enzyme activity during the incubation period on the parameter estimates and the possibility to correct for this were also investigated. The MDCM was in good overall agreement with the IFRMM. Correction for a change in enzyme activity was possible and resulted in a better concordance in CLint estimates. The robustness of the method in coping with different rates of substrate turnover and variable starting concentrations were also demonstrated through Monte Carlo simulations. Furthermore, the limitations imposed by assumptions inherent in the in vitro t½ method were demonstrated both experimentally and by simulations. This study demonstrates that the MDCM is a robust and efficient method for estimating enzyme kinetic variables with high accuracy and precision. The method may potentially be used in a wide range of applications, from pure enzyme kinetics to in vitro-based predictions of the pharmacokinetics of compounds with multiple and/or unknown metabolic pathways.
Estimation of metabolic intrinsic clearance (CLint) is currently included in many drug discovery programs. The most frequently used assay is the “in vitro t½” method (T½M), in which CLint is derived from the monoexponential slope of a single depletion curve (Obach, 1999). This method is used both for ranking compounds with respect to metabolic stability and for the prediction of metabolic clearance in animals and humans. The data are usually obtained from incubations with microsomes or fresh or cryopreserved hepatocytes (Iwatsubo et al., 1997; Obach et al., 1997; Rodrigues, 1997; Ito and Houston, 2005). CLint, defined as the maximum velocity of the metabolic reaction (Vmax) divided by the Michaelis constant (Km), the substrate concentration that yields half of Vmax, is by this means used as the link between fundamental enzyme kinetics and in vivo pharmacokinetic variables (Rane et al., 1977). Although the T½M approach is fast, it is built on the assumption that the initial concentration (C0) is well below Km. This assumption is often valid, but, if not, the method will underestimate CLint and thus underpredict the rate of hepatic clearance in vivo. The basic assumption of C0≪Km is usually not confirmed and may be one of several contributing factors to the tendency of systematic underprediction of hepatic clearance seen in the literature (Carlile et al., 1999; Obach, 1999; Ito and Houston, 2005). The ability to predict clearance via an estimate of CLint is nevertheless good, and the method has frequently shown its value (Rostami-Hodjegan and Tucker, 2007). However, one shortcoming is the fact that CLint is a secondary parameter reflecting a simplified picture of metabolic capacity with no information of the underlying primary parameters, Vmax and Km. The confident quantification of these parameters for specific reactions could improve the assessment of drug-drug interactions, help to define the contributions of individual metabolic pathways, and predict the interindividual variability caused by genetic polymorphism. Assessment of Km in combination with CLint enables the prediction of nonlinear kinetics (concentration and dose-dependent bioavailability and clearance), which may improve the accuracy of the prediction of in vivo pharmacokinetics. Knowledge of both CLint and Km for drug candidates as well as for selected compounds in lead optimization is therefore of great value (Ludden, 1991; Obach and Reed-Hagen, 2002).
The traditional method used for the determination of Vmax and Km for a specified reaction is the initial formation rate of metabolite method (IFRMM), where the Michaelis-Menten equation is fitted to the initial formation rates of metabolite at different substrate concentrations. To obtain the total CLint, Vmax and Km for all individual metabolic pathways need to be estimated. However, many drug compounds are metabolized at multiple positions, and, for new chemical entities, these are usually not identified early in the discovery process. These two factors make the method inappropriate for enzyme kinetic investigations in drug discovery. An alternative approach was suggested where parent compound depletion curves at multiple concentrations are generated. Vmax and Km are then estimated by fitting the Michaelis-Menten equation to all disappearance curves simultaneously (Bousquet-Melou et al., 2002). This method is better suited for investigations of enzyme kinetics in drug discovery, but it has not yet been thoroughly evaluated. In contrast to the T½M, the method generates information of the potential for nonlinear pharmacokinetics behavior and does not rely on the assumption of C0 ≪ Km, reducing the risk for under estimation of CLint. However, both methods involve extended incubation times compared with the IFRMM, raising the potential for enzyme degradation and/or inhibition effects during the incubation period (Houston and Carlile, 1997; Jones and Houston, 2004). This could be accounted for by including an enzyme-activity-change (EAC) variable in the kinetic model used in the regression analysis (Bousquet-Melou et al., 2002).
The main objective of this study was to evaluate the multiple depletion curves method (MDCM) by comparing the results (Vmax, Km, CLint) with those gained by the IFRMM and the T½M. A secondary aim was to investigate the impact of change in enzyme activity on the estimates obtained from depletion-based methods and the possibility to correct for such effects in the data analyses. In this report, we examined seven metabolic reactions in either rat liver microsomes or porcine liver S1 fractions. The data enabled a direct comparison of the MDCM, the IFRMM, and the T½M. Monte Carlo simulation analyses were performed to further investigate the robustness, accuracy, and sensitivity of the MDCM. Similar analyses were performed for investigation of the T½M and the impact of a change in enzyme activity during the incubation period.
Materials and Methods
Materials. The following substrates (short name in parentheses), metabolites, and internal standards were obtained from Sigma-Aldrich (Schnelldorf, Germany): flutamide (FLU), carbamazepine, resorufin (RES), ethoxyresorufin (ERES), benzyloxyresorufin (BRES), diclofenac (DFN), N-phenylanthranilic acid, and dextromethorphan (DXM). 2-OH-flutamide (2FLU) was obtained from Mikromol (Luckenwalde, Germany). Dextrorphan (DXO) and 4′-OH-diclofenac (4DFN) were purchased from BD Gentest (Woburn, MA). Ethylmelagatran (EMEL), N-hydroxymelagatran (NMEL), and melagatran (MEL) were a kind gift from AstraZeneca (Mölndal, Sweden). All other reagents and chemicals were of appropriate grade and purchased from Sigma-Aldrich.
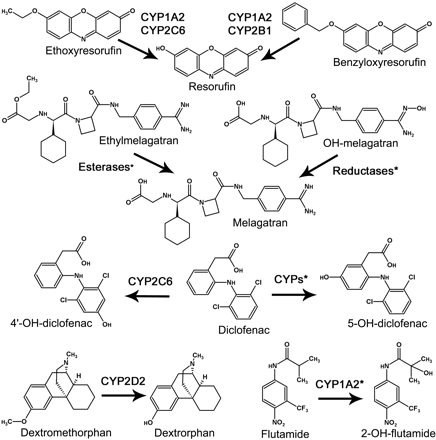
Compound Selection and Enzyme Sources. To enable a valid comparison between the MDCM and the IFRMM, it was important to account for the majority of the metabolic routes. Substrates were therefore selected based on the criteria of a maximum of two dominating measurable metabolic routes contributing to at least 80% of the total metabolism. Ideally, CLint, Vmax, and Km should also cover a wide range. The following seven substrates were selected, and the corresponding metabolites were used for determination of Vmax and Km by the traditional IFRMM: BRES O-dealkylation to RES mediated by CYP1A2 and CYP2B1 (Kobayashi et al., 2002); DFN 4-hydroxylation to 4DFN mediated by CYP2C6 (Kobayashi et al., 2002); DFN 5-hydroxylation to 5-OH-diclofenac (5DFN) mediated by multiple cytochrome P450s (Tang et al., 1999); DXM O-demethylation to DXO mediated by CYP2D2 (Kobayashi et al., 2002); ERES O-deethylation to RES mediated by CYP1A2 and CYP2C6 (Kobayashi et al., 2002); EMEL ester hydrolysis to MEL (specific enzymatic pathway unidentified) (Eriksson et al., 2003); FLU 2-hydroxylation to 2FLU mainly mediated by CYP1A2 (Berson et al., 1993; Fau et al., 1994); and NMEL reduction to MEL (specific enzymatic pathway unidentified) (Eriksson et al., 2003). The reactions are displayed in Fig. 1.
All reactions were investigated in female rat liver microsomes, with the exception of EMEL and NMEL, where male porcine liver S1 fractions were used to include all enzymes involved in the metabolism of these compounds (Clement and Lopian, 2003). The female rat liver microsome fractions were a kind gift from AstraZeneca. Liver S1 fractions were prepared as follows: fresh male porcine (Swedish Landrace) liver was flushed with ice-cold isotonic saline solution to remove blood and to cool the tissue. Pieces of the liver were homogenized in ice-cold KPO4 buffer (0.1 M, pH 7.4) (1:5 v/w) with a ULTRA-TURRAX dispersion unit (IKA, Staufen, Germany) for 30 s at 6500 rpm and then centrifuged at 1000g for 10 min. The supernatant was collected as the S1 fraction and used within 4 h to minimize the risk of enzyme degradation. Preparations were conducted on ice in an 8°C refrigerated room, and S1 fractions were kept on ice until use. Total protein concentration was determined using a Quick Start Bradford kit (Bio-Rad Laboratories AB, Sundbyberg, Sweden) with Ig as a reference protein.
General Incubation Conditions and Sample Treatment. All incubations were conducted by shaking under air at 37°C. The incubation matrices consisted of KPO4 buffer (final concentration 0.1 M, pH 7.4) and selected cell fractions at optimal protein concentration for the respective substrates. Incubations were performed by adding the substrate to the matrix. The reaction was started after 5-min equilibration by adding NADPH to a final concentration of 1 mM. The concentration of organic solvent did not exceed 0.5% in any of the incubations. After termination, samples were centrifuged for 10 min at 10,000g (Minispinplus; Eppendorf AG, Hamburg, Germany), and an aliquot of the supernatant was drawn for sample analysis. When necessary, the aliquot was mixed with water or buffer to mimic the mobile phase of the analytical method. The substrate concentration range investigated in the metabolic assays was limited by the solubility and lower limit of quantitation (LLOQ) of the analytical method for each substrate. Product formation experiments and substrate depletion experiments were conducted in triplicate and sets of five, respectively.
Investigations of linearity between the initial rate of metabolism and protein concentration were examined in the protein concentration interval 0.125 to 0.75 mg protein/ml. The protein concentration and incubation time chosen for each substrate were based on both linearity and a maximum substrate depletion of 15%. Optimal protein concentration and time points for sampling are given for respective substrates in the metabolic assay section.
Enzyme stability during incubation conditions was studied by comparing measurements of the initial reaction velocity after 3, 33, and 63 min of incubation stress. At time point 0, reaction tubes containing enzyme in KPO4 buffer (0.1 M, pH 7.4) were placed in a heated water bath at 37°C. Substrates were added at times 0, 30, and 60 min, and the reactions were initiated after 3 min of preincubation, i.e., 3, 33, and 63 min, by the addition of a cofactor to a final concentration of 1 mM. Time points for sample withdrawal, protein concentration, and sample treatment were as described in the metabolic assay for each substrate.
Protein binding in the incubation media was determined by adding different amounts of substrate to 1 ml of incubation medium (enzyme and 0.1 M KPO4 buffer, pH 7.4) covering a suitable range of concentrations. After 10 min of equilibrium, samples of 100 μl were drawn to measure the total concentration. The remaining medium was separated from proteins and other cellular material by ultrafiltration (10,000g for 20 min) using a Microcon YM-10 filter, cutoff 10,000 mol. wt. (Millipore, Solna, Sweden). The filtrate was analyzed to measure the unbound concentration. To determine unspecific binding to the filter, concentrations were measured in filtered and unfiltered 0.1 M KPO4 buffer, pH 7.4. Other binding to the device (e.g., internal walls) was assumed to be negligible because no significant binding to other experimental equipment was observed. All samples were treated as described in the metabolic assay for each substance. The following concentration ranges were investigated: BRES, 0.020 to 1.5 μM; DFN, 10 to 100 μM; DXM, 0.15 to 15 μM; EMEL, 7.5 to 750 μM; ERES, 0.020 to 2.0 μM; NMEL, 12 to 1200 μM; and FLU, 1 to 30 μM.
Chemical structures and metabolic reactions investigated in this study. *, specific reaction pathway unidentified.
Chemical stability in incubation medium (enzyme and 0.1 M KPO4 buffer, pH 7.4) under incubation conditions was examined by keeping the substance in incubation medium at 37°C. Samples were removed at 0, 20, 40, and 60 min and treated as described in the metabolic assay for each substance.
Metabolic Assays.BRES metabolism. Rat liver microsomes at a final concentration of 0.5 mg/ml were used for BRES assays. Product formation experiments for BRES (23–2500 nM) were conducted for 13.5 min, and samples of 100 μl were drawn at 0, 4.5, 9, and 13.5 min. Substrate depletion experiments for BRES (20–2000 nM) were performed for 60 min, and samples of 50 μl were removed at 0, 5, 10, 15, 20, 30, 40, 50, and 60 min. The reactions were terminated by adding an equivalent of three sample volumes of ice-cold methanol containing ERES as an internal standard. Samples were centrifuged, and the supernatant was then injected into the high-performance liquid chromatography (HPLC) system.
DFN metabolism. Rat liver microsomes at a final concentration of 0.5 mg/ml were used for DFN assays. Product formation experiments for DFN (1.9–440 μM) were conducted for 13.5 min, and samples of 100 μl were drawn at 0, 4.5, 9, and 13.5 min. Substrate depletion experiments for DFN (3.5–350 μM) were performed for 60 min, and samples of 100 μl were removed at 0, 7.5, 15, 22.5, 30, 37.5, 45, 52.5, and 60 min. The reactions were terminated by adding 200 μl of CH3CN containing N-phenylanthranilic acid as an internal standard. Postcentrifugation supernatant aliquots were mixed with an equal amount of sodium acetate buffer (0.75 mM, pH 5.0) before analysis by HPLC.
DXM metabolism. Rat liver microsomes at a final concentration of 0.5 mg/ml were used for DXM assays. Product formation experiments for DXM (0.1–60 μM) were conducted for 13.5 min, and samples of 100 μl were drawn at 0, 4.5, 9, and 13.5 min. Substrate depletion experiments for DXM (0.5–50 μM) were performed for 60 min, and samples of 100 μl were removed at 0, 7.5, 15, 22.5, 30, 37.5, 45, 52.5, and 60 min. The reactions were terminated by adding 350 μl of stop solution (CH3CN, methanol, phosphoric acid, 17:17:4) containing DFN as an internal standard. Samples were centrifuged, and the supernatant was then injected into the HPLC system.
ERES metabolism. Rat liver microsomes at a final concentration of 0.125 mg/ml were used for ERES assays. Product formation experiments for ERES (23–2500 nM) were conducted for 9 min, and samples of 100 μl were drawn at 0, 3, 6, and 9 min. Substrate depletion experiments for ERES (180–2500 nM) were performed for 60 min, and samples of 50 μl were removed at 0, 5, 10, 15, 20, 30, 40, 50, and 60 min. The reactions were terminated by adding an equivalent of three sample volumes of ice-cold methanol containing BRES as an internal standard. Samples were centrifuged, and the supernatant was then injected into the HPLC system.
EMEL metabolism. Porcine liver S1 fractions at a final concentration of 0.3 mg/ml were used for EMEL assays. Both NADH and NADPH at final concentrations of 1 mM were used as cofactors in the assay. In contrast to the general assay procedure, NADH and NADPH were first added to the incubation matrix, and the reactions were started after 5 min of equilibration by adding EMEL. Product formation experiments for EMEL (4.0–1900 μM) was conducted for 13.5 min, and samples of 30 μl were drawn at 0, 4.5, 9, and 13.5 min. Substrate depletion experiments for EMEL (8.5–1400 μM) were performed for 60 min, and samples of 40 μl were removed at 0, 7.5, 15, 22.5, 30, 37.5, 45, 52.5, and 60 min. The reactions were terminated by adding 100 μl of CH3CN. Postcentrifugation supernatant aliquots were diluted with water to adjust the concentration of analytes and CH3CN to a level compatible with the analytical method before analysis by liquid chromatography (LC).
FLU metabolism. Rat liver microsomes at a final concentration of 0.5 mg/ml were used for FLU assays. Product formation experiments for FLU (1.4–57 μM) were conducted for 15 min, and samples of 100 μl were drawn at 0, 5, 10, and 15 min. Substrate depletion experiments for FLU (2.1–130 μM) were performed for 60 min, and samples of 100 μl were removed at 0, 5, 10, 15, 20, 30, 40, 50, and 60 min. The reactions were terminated by adding an equivalent of three sample volumes of CH3CN containing carbamazepine as an internal standard. Postcentrifugation supernatant aliquots were mixed with an equal amount of water before analysis by HPLC.
NMEL metabolism. Porcine liver S1 fractions at a final concentration of 0.3 mg/ml were used for NMEL assays. Both NADH and NADPH at final concentrations of 1 mM were used as cofactors in the assay. In contrast to the general assay procedure, NADH and NADPH were first added to the incubation matrix, and the reactions were started after 5 min of equilibration by adding NMEL. Product formation experiments for NMEL (5.0–2300 μM) were conducted for 13.5 min, and samples of 30 μl were drawn at 0, 4.5, 9, and 13.5 min. Substrate depletion experiments for NMEL (21–2600 μM) were performed for 60 min, and samples of 40 μl were removed at 0, 7.5, 15, 22.5, 30, 37.5, 45, 52.5, and 60 min. The reactions were terminated by adding 100 μl of CH3CN. Postcentrifugation supernatant aliquots were diluted with water to adjust the concentration of analytes and CH3CN to a level compatible with the analytical method before analysis by LC.
Analytical Assays: Instrumentation.Instrumentation for HPLC analysis with UV or fluorometric detection. The HPLC system consisted of a CMA/200 refrigerated microsampler (CMA/Microdialysis, Solna, Sweden) and an LC-10AD pump (Shimadzu, Kyoto, Japan). UV detection was performed using a Spectra 100 UV detector (Thermo Fisher Scientific, Waltham, MA), and an FP-1520 Intelligent Fluorescence Detector (Jasco, Tokyo, Japan) was used for fluorometric (FL) detection. Concentrations of eluted samples were calculated by comparing the peak areas to those of internal standards (when available) by reference to a calibration curve. Data were acquired and evaluated using CSW32 integrating software (DataApex Ltd., Prague, Czech Republic).
Instrumentation for LC analysis with mass spectrometry. The LC system consisted of an HP 1100 series LC pump and column oven (Agilent Technologies Deutschland, Waldbronn, Germany), combined with an HTS PAL injector (CTC Analytics, Zwingen, Switzerland). Mass spectrometry was performed with a triple quadrupole mass spectrophotometer, API4000, equipped with an electrospray interface (Applied Biosystems/MDS Sciex, Foster City, CA). Instrument control, data acquisition, and evaluation were performed using Applied Biosystems/MDS Sciex Analyst 1.4 software.
Sample Analysis of RES, ERES, and BRES. Separation was performed on a ZORBAX SB-CN column (4.6 × 250 mm, 5 μm; Agilent Technologies, Santa Clara, CA) after a sample injection volume of 100 μl. The mobile phase consisted of methanol and KPO4 buffer (pH 7.0, I = 0.02) at a ratio of 2:1. Flow rate was set to 1 ml/min, and all peaks were eluted within 12 min. FL detection was performed using an excitation/emission setup of 530/580 nm for RES analysis and 465/540 nm for ERES and BRES analysis. The method was validated to LLOQs for RES, ERES, and BRES of 0.45, 42, and 3.6 nM, respectively. BRES was used as an internal standard for ERES activity analysis and vice versa.
Sample Analysis of DFN and 4DFN/5DFN. Analyses of DFN and its metabolites were performed using a modified version of the method described by Kaphalia et al. (2006). In brief, samples were separated on a Hypersil Gold C18 column (4.6 × 250 mm, 5-μm particle size; Thermo Fisher Scientific) after a sample injection volume of 100 μl. The mobile phase consisted of CH3CN and 0.75 mM sodium acetate buffer, pH 5.0 at a ratio of 2:3. All peaks were isocratically eluted within 14 min at a mobile phase flow rate of 1 ml/min and detected using UV at 280 nm. A single unidentified peak eluted at 6.25 min was assumed to be 5DFN (Kaphalia et al., 2006). No authentic standard for 5DFN was commercially available, but because the chromatophoric difference between 5DFN and 4DFN is presumed negligible, 4DFN was used as the reference. This practice has successfully been used in previous studies and was verified by controlling the mass balance (Cummins et al., 2002). The method was validated to LLOQs of 20 and 10 nM for DFN and 4DFN/5DFN, respectively.
Sample Analysis of DXM and DXO. Analyses of DXM and DXO were performed using a modified version of the method described by Yu and Haining (2001). In brief, samples were isocratically separated on a ReproSil 100 Phenyl column (4.6 × 250 mm, 5-μm particle size; Dr. Maisch GmbH, Ammerbuch-Entringen, Germany) after a sample injection volume of 100 μl. The composition of the mobile phase was 50% potassium phosphate buffer (0.01 M), pH 5.7 (pH adjusted with 99.9% H3PO4) and 50% CH3CN and MeOH (5:4). All peaks were eluted within 14 min. The mobile phase flow rate was set to 1 ml/min, and FL detection was performed using wavelengths of 280-nm excitation and 310-nm emission. The method was validated to LLOQs of 5.2 and 5.1 nM for DXM and DXO, respectively.
Sample Analysis of EMEL, NMEL, and MEL. Analyses of EMEL, NMEL, and MEL were performed using the method described by Andersson et al. (2005). In brief, LC separations were performed on a revered-phase HyPURITY C18 analytical column (100 mm × 2.1 mm i.d., 5 μm; Thermo Fisher Scientific) at 40°C. The mobile phase consisted of 10% CH3CN, 5 μM acetic acid, and 10 mM ammonium acetate, resulting in a solvent with approximately pH 5. Samples were isocratically eluted at a flow rate of 0.67 ml/min, and all peaks were eluted within 5 min. Samples were detected using mass spectrometry operated under the following conditions: turbo heater temperature (550°C), nebulizer gas (GS1) at 60 psi gauge (psig), turbo gas (GS2) at 70 psig, curtain gas at 30 psig, and an electrospray voltage of 4 kV in positive mode. The orifice voltage was set at 81 V, the collision energy was set at 33 V, and the collision-activated dissociation gas was set at 10 psig. The multiple reaction monitoring transitions of the precursor ions (M + H)+ to the corresponding product ions were m/z 458.2 to 198.2, 446.1 to 249.1, and 430.1 to 233.3 for EMEL, NMEL, and MEL, respectively.
Sample Analysis of FLU and 2FLU. Analyses of FLU and 2FLU were performed using a modified version of the method described by Leibinger and Kapàs (1996). In brief, 50 μl of sample were injected and separated on a Hypersil Gold C18 column (4.6 × 250 mm, 5 μm; Thermo Fisher Scientific). The mobile phase consisted of H2O, CH3CN, and methanol (45:35:25) at a flow rate set to 1.5 ml/min. All peaks were eluted within 10 min. Eluted samples were detected by UV at 300 nm, and the method was validated to LLOQs of 80 and 60 nM for FLU and 2FLU, respectively.
Data Analysis: Protein Binding. The fraction unbound (fu) at optimal protein concentration under incubation conditions was calculated by dividing the substrate concentration after filtration ([Cu]), corrected for unspecific binding to filter, with unfiltered substrate concentration ([C]) (eqs. 1 and 2). 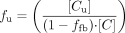
 where [Cub] is the concentration after filtration, [Cb] is the concentration before filtration, measured in the absence of proteins, and ffb is the fraction of unspecific binding to the filter.
where [Cub] is the concentration after filtration, [Cb] is the concentration before filtration, measured in the absence of proteins, and ffb is the fraction of unspecific binding to the filter.
Initial Formation Rate of Metabolite Method. The rates of metabolite appearance at different substrate concentrations were calculated by plotting metabolite concentration versus time. Formation rates were normalized to protein concentration, and the Michaelis-Menten equation (eq. 3) was fitted by nonlinear regression to formation rate versus free substrate concentration. 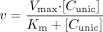 where v is the formation rate, Vmax is the theoretical maximum formation rate, Km is the unbound substrate concentration at half the theoretical maximum formation rate, and [Cuinc] is the unbound substrate concentration in the incubation ([Cuinc] = [C] · fu).
where v is the formation rate, Vmax is the theoretical maximum formation rate, Km is the unbound substrate concentration at half the theoretical maximum formation rate, and [Cuinc] is the unbound substrate concentration in the incubation ([Cuinc] = [C] · fu).
The unbound CLint was calculated by dividing Vmax by Km (eq. 4). 
When more than one reaction was followed (DFN reaction), the sums of the individual CLint values were calculated to obtain a total CLint.
Multiple Depletion Curves Method. Two models were used to describe the rate of substrate depletion. One, not correcting for EAC (MDCM), is given in eq. 5 and one, correcting for EAC described as a monoexponential decay (MDCM + ke), is given in eq. 6. 
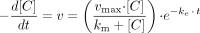 where vmax is the theoretical maximum depletion rate, km is the substrate concentration at half the theoretical maximum depletion rate, [C] is the substrate concentration, and ke is the enzyme activity change constant.
where vmax is the theoretical maximum depletion rate, km is the substrate concentration at half the theoretical maximum depletion rate, [C] is the substrate concentration, and ke is the enzyme activity change constant.
The parameters, vmax and km, were estimated by simultaneous fitting of the equations to all concentration-time profiles using nonlinear regression. The regression was performed with a weighting scheme of 1/([C]2).
Vmax was obtained by dividing vmax with the protein concentration used in incubation (Cp) (eq. 7), and Km was calculated by multiplying km with fu (eq. 8). CLint was then calculated in the same way as in the IFRMM (eq. 4). 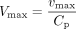

In Vitro t½ Method. The depletion data were also used to determine CLint with the T½M by fitting a first order of disappearance to a single selected depletion data set (eq. 9). A first order of disappearance is obtained by setting [C] = 0 in the denominator of eq.3, which is a fair approximation when [C] is negligible compared with Km.  where Ct is the concentration at time t and k is the disappearance rate constant.
where Ct is the concentration at time t and k is the disappearance rate constant.
CLint was then calculated by dividing the disappearance rate constant with Cp and fu (eq. 10). 
The determinations were done using the data set with the lowest available C0 for each substrate. Furthermore, in consideration of the risk of consistently using a fixed C0 at 1 μM, as commonly adopted, a second determination was done for those reactions where such a data set was available.
All analyses of kinetic data were performed using WinNonlin Professional software version 4.0 (Pharsight, Mountain View, CA). For evaluation and comparison of the goodness of fit for the different methods, Akaike information criterion, visual examination of data, residual plots, and the precision of parameter estimation were used.
Monte Carlo Simulations. A limited analysis of the MDCM robustness, i.e., accuracy and precision, was conducted to further investigate the performance of the method. The experimental variables included in the analysis were the distribution of C0 in relation to Km and the relative turnover during the incubation. A similar analysis was conducted to investigate the size of the estimation error related to the T½M when using a suboptimal C0. In addition, the impact of EAC was investigated.
In both the MDCM and T½M simulations, simulated data were generated according to eq. 6 by using the Runge-Kutta algorithm to solve values from the differential equation. In the precision study, when determining the propagation of errors (noise) from measured data into the final parameters, Monte Carlo simulations were performed with a Gaussian noise added to the generated data points. To determine a relevant noise level, a sample S.D. study of the experimental raw data (concentrations) available was done before the simulations. In the experiments, the concentrations were measured in sets of five, and from each set a standard deviation was calculated. A total of 120 S.D. were determined in this way. It could be concluded from these steps that the relative S.D. was similar over the whole concentration range with an average value of 0.073. A noise level giving this relative S.D. was applied in the Monte Carlo simulations described above.
Parameters were estimated from the generated data by nonlinear regression carried out by an in-house developed Visual Basic program using Levenberg-Marquardts curve-fit algorithm linked to the Runge-Kutta algorithm for the numerical solution of the differential equation.
In the Monte Carlo simulation exercises, data points were weighted by the inverse of the S.D. in the fittings, and the S.D. for the individual estimates was determined. One hundred simulations were made for each parameter combination. The mean and the coefficient of variation of the 100 individual parameter estimates, respectively, were used as measures of accuracy and precision.
MDCM. The simulations were, in analogy with the experimental setup, performed using three starting concentrations (high = 10, medium = 1, and low = 0.1 μM) at each parameter combination. Data at eight equidistant time points in a time interval [0, tinc] for a number of Vmax and Km combinations and with ke = 0 were generated, and the precision was determined according to the procedure described above in analogy to eq. 6. The parameter values used in combinations were 0.5, 0.05, and 0.005 μM/min for Vmax and 50, 5, and 0.5 μM for Km. The tinc was 60 min in all simulations. To normalize the parameters, initial concentrations were expressed as C0/Km, and Vmax was divided by the high initial concentration (=10) to obtain a relative turnover expressed in percentage per minute (% min–1).
T½M. The sensitivity in the parameter estimation to the inherent approximation in eq. 9 as well as the relative turnover of substrate were investigated. Data at eight equidistant time points in a time interval [0, tinc] for a number of C0, Vmax, Km, and ke combinations were generated in analogy to eq. 6. CLint,est was then estimated by fitting eq. 9 to these data, and accuracy in the prediction estimate was expressed as the ratio of estimated CLint (CLint,est) and CLint,true (i.e., Vmax/Km). The precision was then determined according to the procedure described above. Because tinc has an affect on the absolute turnover, CLint,true was converted to in vitro half-life (t½) using eq. 11 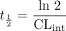 and then made unitless by dividing t½ by tinc, giving the relative turnover (t½ /tinc). Likewise, the initial concentrations were expressed as C0/Km. The parameter values used in combinations were 0.4, 0.2, 0.1, 0.05, 0.02, 0.01, 0.005, and 0.002 ml/mg/min for CLint.true, representing a t½ range of 1.7 to 350 min, 1, 0.5, 0.2, and 0.1 for C0/Km and 0, 0.005, 0.01, and 0.02 min–1 for ke. The tinc was fixed to 60 min in all simulations.
and then made unitless by dividing t½ by tinc, giving the relative turnover (t½ /tinc). Likewise, the initial concentrations were expressed as C0/Km. The parameter values used in combinations were 0.4, 0.2, 0.1, 0.05, 0.02, 0.01, 0.005, and 0.002 ml/mg/min for CLint.true, representing a t½ range of 1.7 to 350 min, 1, 0.5, 0.2, and 0.1 for C0/Km and 0, 0.005, 0.01, and 0.02 min–1 for ke. The tinc was fixed to 60 min in all simulations.
Results
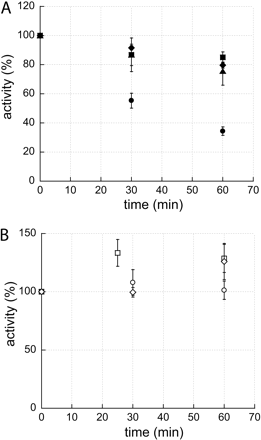
Protein concentrations in incubation, the free fractions in incubation media, and the loss of enzyme activities are summarized in Table 1. Fraction unspecific binding to the filter determined in the protein binding assay ranged from none detected (n.d.) to 0.68 (BRES 0.68, DFN n.d., DXM 0.19, EMEL 0.05, ERES 0.21, FLU 0.14, NMEL n.d.). No unspecific adhesion to laboratory equipment was observed. All compounds, with the exception of BRES, were chemically stable under incubation conditions. Enzyme activity (Fig. 2) ranged from no observable decline (ERES) to an approximate 65% loss (BRES). An increase of the reaction velocity was observed for the two reactions conducted in porcine liver S1 fractions (EMEL and NMEL).
Incubation validation summary showing optimal protein concentration, fu, and percentage enzyme activity after 60-min incubation stress as change of initial reaction rate
Values shown as mean with S.D. (n = 3).
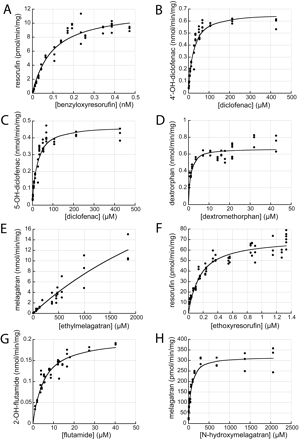
Enzyme Kinetics.Parameters determined with the IFRMM. Primary data from the IFRMM assays are displayed in Fig. 3, and the result is shown in Table 2. IFRMM data for all reactions showed monophasic, Michaelis-Menten behavior, and no more complex models were necessary to describe the data. Vmax values covered more than three orders of magnitude from 12.0 (BRES) to 42,800 nmol/min/mg protein (EMEL). The Km values covered more than four orders of magnitude from 0.0937 (BRES) to 4710 μM (EMEL). For DFN, where two metabolites were formed, the mean of 4DFN and 5DFN Km values and the sum of the Vmax values of the individual reactions were used in further comparisons between the IFRMM and the MDCM. The Km values for these two reactions were very similar, making this approximation reasonable. CLint values, calculated from Vmax and Km determinations, covered approximately two orders of magnitude from 9.10 (EMEL) to 836 ml/min/g protein (DXM).
Summary for enzyme kinetic variables obtained in this study with the IFRMM, MDCM, or MDCM + ke enzymatic activity variable (ke) and the in vitro T1/2M
Values are shown as means with S.E.
Enzyme activity, displayed as percentage change of initial reaction rate, versus time of incubation stress. Enzyme activity shown as mean values of triplicates with S.D. A, reactions catalyzed by unstable enzyme systems; benzyloxyresorufin (•), flutamide (▪), diclofenac (♦), and dextromethorphan (▴). B, reactions catalyzed by stable enzyme systems; ethoxyresorufin (○), ethylmelagatran (□), and N-hydroxymelagatran (⋄).
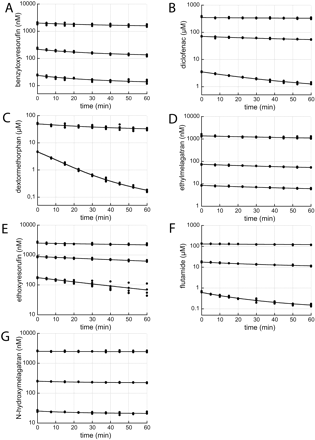
Parameters determined with the MDCM. The data were well described by the given equations under Materials and Methods. More complex models, e.g., two enzymes model, were also tested but did not converge. Primary data from MDCM metabolic investigations are shown in Fig. 4. Results from determinations made with the MDCM (eq. 5) are shown in Table 2. Vmax covered more than four orders of magnitude from 11.8 (BRES) to 36,100 nmol/min/mg protein (EMEL). The Km values covered four orders of magnitude from 0.179 (BRES) to 2340 μM (EMEL). CLint values, calculated from Vmax and Km determinations, covered two orders of magnitude from 1.55 (EMEL) to 311 ml/min/g protein (ERES). The result from determinations made with the MDCM, including EAC (MDCM + ke) (eq. 6), is shown in Table 2. Vmax covered three orders of magnitude from 26.9 (BRES) to 46,900 nmol/min/mg protein (EMEL). The Km values covered four orders of magnitude from 0.166 (BRES) to 2340 μM (EMEL). CLint values, calculated from Vmax and Km determinations, covered two orders of magnitude from 2.01 (EMEL) to 358 ml/min/g protein (ERES). Compensation for chemical instability was done for both methods in the case of BRES.
CLint determined with the T½M. The result from determinations made with the T½M (eqs. 9 and 10) is shown in Table 2. CLint determinations done with the lowest available C0 for respective substrate (BRES, 0.02 μM; DFN, 3 μM; DXM, 5 μM; EMEL, 9 μM; ERES, 0.12 μM; FLU, 0.5 μM; and NMEL, 20 μM) ranged from 8.86 (NMEL) to 71.5 ml/min/g protein (ERES). A second analysis, with a C0 close to 1 μM, could be performed for FLU (1.4 μM; data not shown), BRES (1 μM), and ERES (1 μM). This resulted in reductions in CLint estimates of approximately 1.5-fold for the FLU reaction and 3-fold for the BRES and ERES reactions.
Monte Carlo Simulations.Accuracy and precision analysis of the MDCM. The accuracy and precision of the estimates (Vmax and Km) were good for six of the nine tested combinations of relative initial concentration (C0/Km) and relative turnover (% min–1). Of the remaining three data sets, two suffered from poor estimates, and in one the regression did not converge (Table 3). The best accuracy in estimates (1.00–0.97) was obtained for the highest relative initial concentration series (20-2-0.2), even though the precision decreased at the lowest tested relative turnover (0.05% min–1). High relative turnover (5% min–1) was also related to good accuracy in the estimations (1.00–1.16). At the lowest relative initial concentration and relative turnover, estimations were not possible.
Summary of the Monte Carlo simulation study investigating the robustness of the multiple depletion curves method
Accuracy and precision (estimated value/true value ± coefficient of variation) of the estimated kinetic variables, Vmax and Km, at different relative initial concentration levels, C0/Km (high-medium-low), and relative turnover (% min–1).
Accuracy and precision analysis of the T½M. The accuracy [estimation error (%)] of CLint estimates using the T½M was highly dependent both on initial concentration-relative Km (C0/Km) and relative turnover, i.e., half-life divided by time of incubation (t½ /tinc) (Fig. 7A). The accuracy decreased rapidly with increasing C0/Km and t½ /tinc ratios. The C0/Km ratio of 1 showed a bias greater than 40% at relatively low t½ /tinc ratios (>0.3). The precision was only dependent on relative turnover and decreased dramatically with increasing t½ /tinc ratios.
Effect of EAC on CLint estimations using the T½M. The effect of EAC on the accuracy [estimation error (%)] of CLint estimates using the T½M was simulated for a reaction with a C0/Km ratio of 0.1 (Fig. 7B). The estimation error was highly dependent on the EAC constant, ke. A ke value of 0.005, 0.01, and 0.02 (representing an approximate loss of activity after 60 min of 25, 45, and 70%, respectively) resulted in a bias of 10, 15, and 40%, respectively. The estimation error was essentially independent of the relative turnover.
Substrate saturation plots, from initial formation rate data. Actual data points and Michaelis-Menten model fitted curves are displayed. A, resorufin formation from benzyloxyresorufin; B, 4′-OH-diclofenac formation from diclofenac; C, 5-OH-diclofenac formation from diclofenac; D, dextrorphan formation from dextromethorphan; E, melagatran formation from ethylmelagatran; F, resorufin formation from ethoxyresorufin; G, 2-OH-flutamide formation from flutamide; and H, melagatran formation from N-hydroxymelagatran.
Discussion
The major objective of this study was to validate the MDCM in terms of accuracy and precision in estimating CLint as well as the underlying kinetic parameters, Vmax and Km, using the conventional IFRMM as a reference. The validation was done both through experimental work and by means of Monte Carlo simulations. A comparison was also made with the simple T½M. The latter method was also explored in terms of its sensitivity to the basic assumption inherent in the method, i.e., start concentration C0≪Km. A secondary aim was to explore the impact of a change in enzyme activity during the incubation on the parameter estimates and the possibility to account for this in the data analyses.
Results from the MDCM were in good overall agreement with those from the traditional IFRMM in its determinations of Vmax, Km, and CLint (Fig. 5). With few exceptions (Km and CLint value for DXM reaction), all of the estimated parameters were within or almost within a 2-fold difference. The practice of regarding multiple kinetic pathways with equivalent Km values as a single reaction, described by that Km value and the sum of all individual Vmax values, was valid in the case of DFN. The parameter values estimated by the MDCM corresponded very well with the combined values of the 4DFN and 5DFN reactions derived from the IFRMM. The inconsistency seen in the case of DXM may be explained by an influence of N-demethylation to 3-methoxymorphinan. This reaction has previously been reported to be a minor metabolic pathway in Sprague-Dawley rats but may influence the overall parameters estimated by the MDCM (Kerry et al., 1993). In addition, the IFRMM results showed a general pattern of biphasic behavior (Fig. 3D), indicating that a second enzymatic system may contribute to the DXO formation. If so, this could also explain the discrepancy between the two methods, but no support for additional systems could be found in the literature. The IFRMM could not be used as a reference to MDCM for FLU and NMEL because, surprisingly, the measured metabolites only represented 40 and 20%, respectively, of the total disappearance. A recent study identified several metabolites in rats, supporting the argument that FLU are metabolized via multiple pathways (Tevell et al., 2006). To date, no such results have been presented for NMEL. However, this illustrates the strength with the MDCM method when the main purpose is to estimate the overall enzyme kinetic profile, i.e., total Vmax, apparent Km, and total CLint, especially for new chemical entities when the metabolism of the compounds is not fully characterized and the metabolic pathways are not known. When multiple kinetic pathways are present, the MDCM provides useful information of the overall kinetics without prior knowledge of metabolic pathways. These “hybrid” parameters can then be used, e.g., to scale clearance and to predict nonlinearity in vivo.
As expected, the Monte Carlo simulations conducted to investigate the robustness of the MDCM showed that optimal conditions were met when the initial concentrations covered Km and the relative turnover was high. A more interesting finding was that these two factors compensated for each other under suboptimal conditions. In brief, if the C0 range was favorable, it could, to some extent, compensate for a low relative turnover and vice versa (Table 3). This suggests that it is not absolutely necessary to include a concentration well above Km for accurate estimations as long as the turnover is sufficiently high. This is highly relevant because solubility issues often prevent the use of concentrations sufficiently high to reach Vmax when using the IFRMM. For the opposite situation, i.e., for compounds with a low turnover, an advantageous C0 range could still generate accurate parameter estimations as was demonstrated for the data set with the lowest relative turnover (0.05% min–1).
CLint determinations made with the T½M using available data sets with the lowest C0 were essentially consistent with the results from the MDCM (Fig. 6A). The issue of conducting the T½M at a fixed C0 was well illustrated by the decrease in CLint estimates for the three compounds with low Km (BRES, ERES, and FLU) when using a C0 close to 1.0 μM (Fig. 6B). The simulation study confirmed this and also showed the significance of turnover (Fig. 5A). High relative turnover reduced the effect of a suboptimal C0. This is due to the fast decline in concentration bringing the substrate concentration quickly into the linear (i.e., monoexponential) concentration range. Experimentally, this was seen in the case of DXM, where the C0 value for the lowest data set were close to the apparent Km for the reactions but the steep depletion curve still enabled an accurate determination with the T½M. Overall, the simulation study clearly illustrated that the T½M is applicable and highly appropriate when C0 is negligible in comparison to Km (C0/Km ≤ 0.1), although the accuracy of the method decreased slightly at lower turnover (>1). Systems with higher C0/Km ratios were associated with decreased errors and were more susceptible to low turnover. It should also be highlighted that the precision was only dependent on turnover and decreased dramatically with higher t½ /tinc ratios. This is logical, because low turnover results in a low signal to noise ratio.
Substrate depletion plots. Points correspond to observed concentrations. The solid lines represent model fitted data from the regression analyses using the multiple depletion curves method including correction for loss in enzyme activity (MDCM + ke). A, benzyloxyresorufin; B, diclofenac; C, dextromethorphan; D, ethylmelagatran; E, ethoxyresorufin; F, flutamide; and G, N-hydroxymelagatran.
Plots of kinetic parameters estimated from depletion data using the multiple depletion curves method without (MDCM) or with enzyme activity change variable (MDCM+ ke) versus estimations from initial formation rate data (IFRMM). The solid and the dashed lines represent the line of unity and a 2-fold range, respectively. Error bars display respective S.E. values. A, Vmax determinations using MDCM; B, Vmax determinations using MDCM + ke; C, Km determinations using MDCM; D, Km determinations using MDCM + ke; E, CLint determinations using MDCM; and F, CLint determinations using MDCM + ke.
The secondary objective of this study was to investigate the impact of EAC on the parameter estimations. The intent of the experimental part was to estimate the degree of loss in activity to be expected when performing the depletion assays and to identify possible differences between the enzymatic systems used. Because the potential effect of the substrates on the loss of enzyme activity was not covered by this experimental setup, the data could not be directly used as ke in the MDCM regression analysis. Large differences in instability were seen, and the level of enzyme activity loss after 60 min of incubation stress ranged from 0 to more than 60%, reflecting the different enzyme systems and isoforms involved in the metabolism of the substrates in the study. This variability also indicates that individual investigations must be conducted, because there is no generally applicable compensation for EAC. For the reactions using liver S1 fractions, the activity increased after the first measurement, possibly because the enzymes in the incubation matrix were not fully recovered from the cooling process before the first reaction was started. The correction of EAC in the MDCM had an inconsistent effect on the primary variables (Vmax and Km), but it improved the overall accuracy of CLint (Fig. 5) compared with the IFRMM. However, the precision decreased for CLint, whereas it increased for Km. No clear trend for Vmax was seen. Overall, the correction of EAC improved the agreement of the data with the IFRMM. Further support of our findings regarding the effect of EAC was provided by the simulations with the T½M (Fig. 7B). The impact of EAC could, to a major extent, explain the remaining differences between the T½M and the MDCM + ke. The observed estimation error seems to be the sum of the effects of relative turnover and EAC. This may be explained by the fact that the EAC systematically decreases all systems proportionally over time. Because the CLint estimations using the MDCM-ke were in better overall agreement with the IFRMM than the MDCM (as seen in Fig. 5, E and F), we consider that the T½M determinations would also benefit from an EAC correction. The reasons for EAC can be numerous, such as enzyme degradation, damage from NADPH-generated radicals, cofactor depletion, and substrate and/or metabolite inhibition. In simpler enzyme systems such as cell fractions and purified enzymes, the risk of inhibition is greater than in the in vivo situation, because phase II metabolism is inactive or missing (Masimirembwa et al., 2003; Jones et al., 2005). It has also been reported that enzyme degradation positively correlates with increased enzyme concentration (Jones and Houston, 2004). The latter is important to keep in mind because increasing the protein concentration to boost substrate turnover is appealing when using substrate depletion approaches.
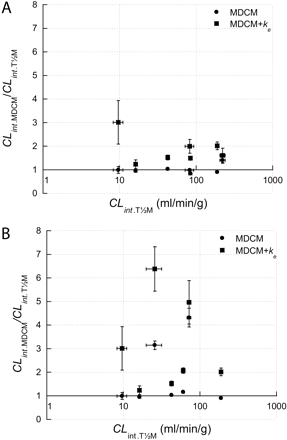
Comparison of CLint estimations determined with the multiple depletion curves method without (MDCM) (•) or with enzyme activity change variable (MDCM + ke) (▪) versus CLint values determined using the in vitro t½ method (T½M). CLint estimations are shown as mean values with S.E. A, CLint values are determined with T½M using the data set with the lowest initial substrate concentration available. B, visualization of the effect on accuracy when using a data set close to 1 μM for the studied reactions with low Km values.
Results from the MDCM are specific for the enzymatic system under study, and the method can therefore be adapted to the purpose. When applied to mixed enzyme systems, the method will provide information on the overall kinetics, where the parameters obtained represent a conglomerate of all reactions present. Like all depletion-based methods, the MDCM has difficulty in distinguishing individual enzymatic routes. If this is the purpose, the method could very well be applied to single-enzyme systems (e.g., recombinant cytochrome P450s), although it was not studied here. When the objective of a study is to estimate overall enzyme kinetics, the MDCM is superior to the IFRMM. In early drug discovery, the metabolic fate of compounds is not known, which automatically disqualifies the use of the IFRMM. Still, for compounds with known metabolic pathways (e.g., drug candidates), the IFRMM requires chemical synthesis and the development of quantitative bioanalytical methods for all of the metabolites. Even so, the IFRMM suffers from potential drawbacks such as sequential metabolism of the primary metabolites, which needs to be compensated for. In contrast to the T½M, the MDCM can be used to calculate Vmax and Km and is not restricted by potential errors related to assumptions that may affect the validity of the method. However, as with depletion methods in general, the MDCM is dependent on a certain degree of turnover relative to the experimental noise.
Estimation error (%) in recovered CLint values using the in vitro t½ method (T½M) versus relative turnover, i.e., half-life related to time of incubation (t½ /tinc). Error bars display S.E. values. A, estimation error (%) dependence of relative initial concentration (C0/Km). C0/Km = 0.1 (▴); C0/Km = 0.2 (♦); C0/Km = 0.5 (▪); and C0/Km = 1 (•). B, estimation error (%) dependence of enzyme activity change at C0/Km = 0.1, described by a first-order elimination constant (ke). ke = 0.02 (▵); ke = 0.01 (⋄); ke = 0.005 (□); and ke = 0 (○).
The overall conclusion from this study is that the MDCM can be used to precisely and accurately estimate enzymatic variables governing overall metabolism. We also expect the method to be widely applicable, because the numerical range for the variables studied (Vmax, Km, and CLint) were large and the Monte Carlo simulation study demonstrated that factors like C0 range and metabolic turnover compensate for each other under suboptimal conditions. Correction for EAC was possible and improved the accuracy in the estimations. Although the experimental setup used in this study was fairly sample rich and hence not optimal for screening purposes, it is still expected that the method will perform well with a reduced number of samples. However, an extended study is needed to find the optimal experimental setup for such an application.
Finally, the MDCM may potentially be used in a wide range of applications, from pure enzyme kinetics to in vitro-based predictions of the pharmacokinetics of compounds with multiple and/or unknown metabolic pathways.
Footnotes
-
This work was supported by AstraZeneca R&D Mölndal (Mölndal, Sweden).
-
Article, publication date, and citation information can be found at http://dmd.aspetjournals.org.
-
doi:10.1124/dmd.108.021477.
-
ABBREVIATIONS: CLint, intrinsic clearance; Vmax, maximum velocity of the metabolic reaction; Km, Michaelis constant; T½M, in vitro t½ method; IFRMM, initial formation rate of metabolite method; EAC, enzyme-activity-change; MDCM, multiple depletion curves method; FLU, flutamide; RES, resorufin; ERES, ethoxyresorufin; BRES, benzyloxyresorufin; DFN, diclofenac; DXM, dextromethorphan; 2FLU, 2-OH-flutamide; DXO, dextrorphan; 4DFN, 4′-OH-diclofenac; EMEL, ethylmelagatran; NMEL, N-hydroxymelagatran; MEL, melagatran; 5DFN, 5-OH-diclofenac; LLOQ, lower limit of quantitation; HPLC, high-performance liquid chromatography; LC, liquid chromatography; FL, fluorometric; psig, psi gauge; n.d., none detected; fu, fraction unbound; ffb, binding to filter.
- Received March 14, 2008.
- Accepted September 24, 2008.
- The American Society for Pharmacology and Experimental Therapeutics