Paroxetine (Paxil) is a widely used selective serotonin reuptake inhibitor antidepressant that is indicated for the treatment of major depressive disorder, obsessive compulsive disorder, panic disorder, generalized anxiety disorder, social anxiety disorder, and post-traumatic stress disorder.

Paroxetine is an established perpetrator of drug-drug interactions (DDIs) when coadministered with agents whose clearance is largely dependent on the activity of cytochrome P450 2D6 (CYP2D6). Examples of characterized clinical interactions with paroxetine include its effects on the kinetics of desipramine (Brøsen et al., 1993; Alderman et al., 1997), perphenazine (Özdemir et al., 1997), metoprolol (Hemeryck et al., 2000), risperidone (Spina et al., 2001), and atomoxetine (Belle et al., 2002), where the clearance of the victim drugs is impaired by 5- to 8-fold. In addition, paroxetine displays nonlinear accumulation kinetics with steady-state exposures exceeding projections from single-dose kinetics by ∼5-fold in CYP2D6 extensive metabolizers but not in CYP2D6 poor metabolizers (Kaye et al., 1989; Sindrup et al., 1992). This finding has been attributed to metabolic saturation following multiple dosing (Sindrup et al., 1992), although supporting evidence at the enzyme kinetic level is lacking. In vitro studies have reproducibly demonstrated potent inhibition of human liver microsomal CYP2D6 activity via an apparent competitive mechanism (von Moltke et al., 1995; Otton et al., 1996; Hemeryck et al., 2001). However, attempts at in vitro-in vivo extrapolation (IVIVE) of interaction magnitude under the assumption of reversible inhibition have been largely unsuccessful, even when nonspecific microsomal binding in vitro was considered (Hemeryck et al., 2001) or empirical approaches such as application of total plasma or even total intrahepatic concentrations of paroxetine were used in the predictions (von Moltke et al., 1995; Hemeryck et al., 2000).

Recent data have provided evidence for mechanism-based inactivation (MBI) of CYP2D6 by paroxetine (Bertelsen et al., 2003). Paroxetine produced a concentration- and time-dependent inhibition of human liver microsomal CYP2D6 activity in vitro, as measured by dextromethorphan O-demethylation rate. Kinetic analysis revealed that paroxetine produced a metabolism-dependent rapid loss of activity of the enzyme with a half-life of inactivation of 4 min (k_inact 0.17 min^-1), and biochemical evidence for metabolite-intermediate complexation via a carbene-heme complex with CYP2D6 (Bertelsen et al., 2003).

Whereas in vitro-in vivo scaling approaches for reversible inhibition of P450 enzymes have been extensively described over the last decade and applied in the prediction of drug-drug interactions, mathematical models for scaling interactions resulting from mechanism-based inhibition have only recently been described, with relatively fewer reported examples illustrating their predictive utility. Of notable mention are the reasonably successful predictions of the interactions perpetrated by fluoxetine, diltiazem, clarithromycin, verapamil, and the HIV protease inhibitors with CYP3A4 substrates using a mathematical model of mechanism-based inhibition developed by Hall and colleagues (Mayhew et al., 2000; Wang et al., 2004; Ernest et al., 2005). In vitro-in vivo extrapolations using this model require a formal kinetic analysis of inactivation by the perpetrator agent to determine the potency of inactivation (K_I) and maximal inactivation rate (k_inact). An estimate of the enzyme-available concentration of the inhibitor is necessary (as for scaling models for reversible inhibition). In addition, an estimate of the in vivo degradation rate (k_degrad) of the enzyme in humans is needed.

In this report, we describe the application of the scaling model for mechanism-based inhibition in predicting the pharmacokinetic consequences of CYP2D6 inactivation by paroxetine from in vitro data. Specifically, we describe predictions of 1) the nonlinear accumulation kinetics of paroxetine resulting from autoinhibition of clearance; and 2) the magnitude of drug-drug interactions of paroxetine with CYP2D6 substrate victim drugs. In addition, we have characterized the sensitivity of these predictions to estimates of model inputs that are nearly impossible to determine directly in humans and, therefore, are associated with the greatest uncertainty: in vivo enzyme degradation rate and the in vivo enzyme-available inhibitor concentration. The implications of these findings for assessment of clinical risk associated with mechanism-based inhibitory DDIs are discussed.

Materials and Methods

Scaling Model. The following mathematical model has been previously derived for IVIVE of drug interactions resulting from MBI (Mayhew et al., 2000): 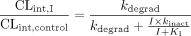In eq. 1, CL_int,I and CL_int,control are the intrinsic clearance of the metabolic pathway of the victim drug in the presence and absence of the mechanism-based inactivator (concentration I). The inactivation rate constant k_inact (maximal inactivation rate at saturating concentration of the inactivator) and the potency K_I (inactivator concentration at which half-maximal inactivation rate is achieved), which are typically measured in vitro, are the primary kinetic parameters describing the MBI process, and k_degrad represents the first-order rate constant for degradation (turnover) of the enzyme in vivo. If the victim drug is dosed orally, completely absorbed, and cleared entirely by hepatic metabolism by the inactivated enzyme, the apparent oral clearance (CL_po) should equal CL_int, and the fractional decrement in oral clearance (FDCL) can thus be described as: 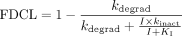In the application of this model to scaling DDIs perpetrated by paroxetine via MBI of CYP2D6, it was assumed that non-CYP2D6 clearance mechanisms of the victim drugs of interest (desipramine, risperidone, perphenazine, atomoxetine, (S)-metoprolol, and (R)-metoprolol) were unaffected by paroxetine treatment. Thus, the fractional decrement of total oral clearance (FDCL_tot) was calculated as follows, where f_2D6 represents the fractional contribution of CYP2D6 to the overall oral clearance of the specific victim drug: The magnitude of the DDI (fold-increase in victim drug AUC) was predicted as follows: 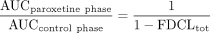The above described approach was also used to assess the extent of nonlinear accumulation of paroxetine following multiple dose administration, with the only conceptual difference being that paroxetine is considered as both the perpetrator and the victim drug in the analysis (i.e., autoinactivation).

Estimation of Model Inputs. As prerequisites to the IVIVE exercise, the following model inputs were estimated: k_inact, K_I, k_degrad, I, and f_2D6.

In vitro kinetic analysis of MBI of CYP2D6 by paroxetine has been previously described (Bertelsen et al., 2003), and the following kinetic parameters were reported: k_inact of 0.17 min^-1 and K_I of 4.85 μM. A human liver microsomal protein concentration of 2.5 mg/ml was used in the preincubation with paroxetine in these studies of time- and concentration-dependent effects on CYP2D6 activity. The estimated unbound fraction of paroxetine at the microsomal protein concentration used in the kinetic MBI studies is 0.065, extrapolated from the results of previously described human liver microsomal binding experiments (Hemeryck et al., 2001). Thus, the unbound K_I for paroxetine inactivation of CYP2D6 was determined as 0.315 μM. Both “total” and “unbound” K_I estimates (4.85 μM and 0.315 μM, respectively) were explored as inputs for scaling to assess the utility of nonspecific binding considerations in the estimation of inhibitor potency.

An indirect approach was used to determine k_degrad for CYP2D6 from the time course of return of CYP2D6 activity (measured as the dextromethorphan/dextrorphan urinary metabolic ratio) to baseline following discontinuation of paroxetine administration (20 mg/day for 10 days) in healthy volunteers (Liston et al., 2002). In the aforementioned study, CYP2D6 activity returned to baseline after cessation of paroxetine administration, with a half-life of 69.6 h. This half-life of return of CYP2D6 activity to baseline should reflect two processes: CYP2D6 turnover half-life and paroxetine steady-state half-life [18.3 h after dosing at 20 mg/day (Kaye et al., 1989)]. The CYP2D6 turnover half-life was thus determined using a noncompartmental deconvolution (component analysis) approach. Deconvolution of the mean residence time of paroxetine at steady state of 26.4 h (18.3/0.693) from the mean time of return of CYP2D6 activity to baseline of 100.4 h (69.6/0.693) afforded a mean CYP2D6 degradation time of 74 h (100.4–26.4), translating to a CYP2D6 degradation half-life of 51 h (0.693 × 74) and a first-order degradation rate constant k_degrad of 0.0136 h^-1 for CYP2D6.

The inhibitor concentration (I) was estimated as the unbound steady-state average concentration of paroxetine from total systemic exposures that were either measured in the specific drug-drug interaction studies or reported in previously published literature on the clinical pharmacokinetics of paroxetine (Kaye et al., 1989), and an unbound fraction (f_u) of 0.05 in human plasma (Kaye et al., 1989). Other estimates of inhibitor concentration including the total systemic concentration and the steady-state maximum unbound concentration at the inlet to the liver (estimated using eq. 5, which includes the steady-state systemic paroxetine C_max and an additive portal venous “absorption” component as described by Kanamitsu et al., 2000) were also evaluated as alternative inputs to the model. 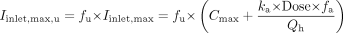For application of eq. 5, the absorption rate constant (k_a) for paroxetine was estimated as 0.01 min^-1 using eq. 6, based on a mean T_max of 5 h and a half-life of 23 h (elimination rate constant k_el of 0.03 h^-1). Complete absorption (f_a = 1) of paroxetine was assumed based on the human absorption/disposition of paroxetine (Kaye et al., 1989), and a hepatic blood flow (Q_h) of 1500 ml/min was assumed (Davies and Morris, 1993).

The fractional contribution of CYP2D6 to the overall oral clearance of each victim drug (f_2D6) was estimated from its clinical pharmacokinetics in CYP2D6 extensive metabolizers and poor metabolizers (Table 1) as follows, where CL_{po,CYP2D6 PM} (or AUC_{CYP2D6 PM}) and CL_{po,CYP2D6 EM} (or AUC_{CYP2D6 EM}) are literature values of the respective apparent oral clearance values (or area under the plasma concentration-time curve following an oral dose) of the victim drug [atomoxetine (Sauer et al., 2003), desipramine (Brøsen et al., 1993), (R)-metoprolol (Lennard et al., 1983), (S)-metoprolol (Lennard et al., 1983), paroxetine (Sindrup et al., 1992), perphenazine (Dahl-Puustinen et al., 1989), or risperidone (Huang et al., 1993)] in the poor metabolizer and extensive metabolizer subpopulations:

Sensitivity Analysis. The sensitivities of the model-derived predictions of drug interaction magnitude (fold-increase in victim drug AUC) to uncertainties in estimates of CYP2D6 degradation half-life and enzyme-available inhibitor concentration (I) were simulated over a wide range of relevant values for these input parameters (CYP2D6 half-life values of 10–100 h, and enzyme-available paroxetine concentrations of 1–1000 nM) for victim drugs, with varying relative contributions of CYP2D6 to overall oral clearance (f_2D6 ranging from 0.5–1.0), using eqs. 2, 3, 4. An unbound K_I of 0.315 μM was used for these simulations.

Results

Prediction of Nonstationary Pharmacokinetics of Paroxetine. Steady-state average plasma concentrations of 35 to 42.5 ng/ml are achieved following dosing with paroxetine at 20 to 30 mg q.d., translating to unbound systemic exposures of 5.3 to 6.5 nM (Kaye et al., 1989; Sindrup et al., 1992). Application of the scaling model with the previously described input parameters (k_degrad of 0.0136 h^-1, k_inact of 0.17 min^-1, and an unbound K_I for CYP2D6 inactivation of 0.315 μM) suggests that in patients receiving paroxetine at 20 to 30 mg q.d. doses, 93% of CYP2D6 will be inactivated. Upon consideration of paroxetine's f_2D6 of 0.86, the net decrement in paroxetine oral clearance at steady state as a consequence of autoinactivation of CYP2D6-mediated hepatic metabolism is predicted to be 80%, translating to a predicted accumulation ratio that is 5 times that expected if the kinetics were time-independent. This prediction is in excellent agreement with the observed 4.9- to 5.7-fold greater than expected accumulation following multiple dose administration of paroxetine at 20 to 30 mg q.d. in clinical pharmacokinetic studies (Kaye et al., 1989; Sindrup et al., 1992).

However, when nonspecific microsomal binding of paroxetine in vitro was not considered in the scaling process (that is, a “total” K_I value of 4.85 μM was used as input to the model), the predicted percentage loss of CYP2D6 activity following multiple dose administration of paroxetine at 20 to 30 mg q.d. was only 45 to 50%, translating to an approximately 40% decrement in paroxetine steady-state oral clearance, and accumulation that is 1.7-fold in excess of that expected from the single-dose kinetic profile. Failure to consider nonspecific microsomal binding in vitro therefore resulted in an approximately 3-fold underprediction of the extent of nonlinearity in accumulation of paroxetine.

Application of total systemic steady-state average concentrations of paroxetine [106–130 nM following dosing with paroxetine at 20 to 30 mg q.d. (Kaye et al., 1989; Sindrup et al., 1992)] or estimated steady-state maximum unbound concentrations of paroxetine at the inlet to the liver (∼27–40 nM following dosing with paroxetine at 20 to 30 mg q.d.), calculated using eq. 5 as inputs to the scaling model, did not increase predictive accuracy (a 6- to 7-fold greater than expected accumulation was predicted, compared with a 5-fold prediction using steady-state average systemic unbound concentrations).

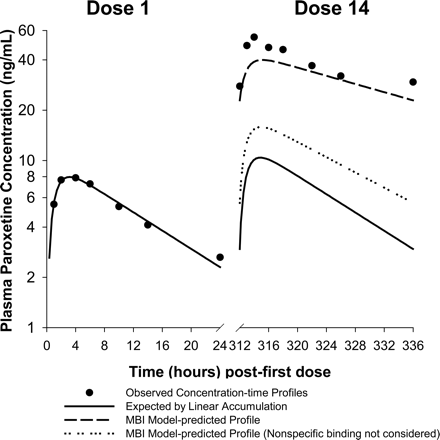
The performance of the scaling model in predicting the steady-state kinetics of paroxetine from the single-dose kinetic profile is illustrated in Fig. 1. For purposes of this exercise, previously published data on the single-dose kinetics of paroxetine (Sindrup et al., 1992) were fitted to a one-compartment pharmacokinetic model, and the following parameters were estimated: first-order absorption rate constant (k_a), 0.908 h^-1; apparent volume of distribution (V/F), 3087 liters; and elimination rate constant (k_el), 0.063 h^-1. The expected steady-state profile following administration of 14 daily doses of 30 mg was traced by superposition of the fitted single-dose kinetic profile (WinNonlin Enterprise version 3.2 software; Pharsight, Mountain View, CA), assuming linear accumulation kinetics. These profiles for the 1st and 14th dosees are represented in Fig. 1 by solid lines. Assuming a hepatic blood flow of 21 ml/min/kg (Davies and Morris, 1993), the impact of autoinactivation on the systemic clearance and oral bioavailability of paroxetine at steady state were estimated from the model-predicted fractional decrement in apparent oral clearance (intrinsic clearance), in the context of a well stirred pharmacokinetic model (Wilkinson and Shand, 1975). Assuming that autoinactivation does not alter volume of distribution [but would alter the apparent volume of distribution (V/F) due to alteration of the bioavailability, F] or absorption kinetics, and that changes in systemic clearance will be reflected as changes in elimination half-life, the following pharmacokinetic parameters for paroxetine post-CYP2D6 inactivation were derived: apparent volume of distribution (V/F), 1397 liters; and elimination rate constant (k_el), 0.0282 h^-1. The corresponding superpositioned steady-state profile is represented in Fig. 1 by a dashed line profile and is in reasonably good agreement with the observed steady-state pharmacokinetic data. In contrast, when nonspecific microsomal binding is not considered in the scaling, the resulting pharmacokinetic parameter estimates [apparent volume of distribution (V/F) 2262 liters; and elimination rate constant (k_el) 0.0525 h^-1] predict a steady-state profile (represented by the dotted line) that substantially underpredicts the observed extent of accumulation.

• Download figure
• Open in new tab
• Download powerpoint

Fig. 1.

Prediction of nonstationary kinetics of paroxetine by the MBI scaling model. Symbols represent the observed plasma concentration-time data on days 1 and 14 of paroxetine administration at 30 mg q.d., from Sindrup et al. (1992). Solid lines are the best fit pharmacokinetic curve for the day 1 data and the expected day 14 profile derived by superpositioning. The dashed and dotted lines represent the scaling model-predicted day 14 profile from in vitro MBI kinetic parameters and the day 1 profile, with and without consideration of in vitro nonspecific microsomal binding of paroxetine, respectively. Note the underprediction of nonlinearity in accumulation kinetics of paroxetine when in vitro microsomal binding is ignored during scaling.

Prediction of Drug Interaction Magnitudes. The results of in vitro-in vivo extrapolation of drug interaction magnitude for CYP2D6 substrate victim drugs upon coadministration of paroxetine are detailed in Table 2. The scaling model predicts that administration of 20 to 30 mg daily doses of paroxetine results in a >90% loss of CYP2D6 activity (FDCL_2D6 0.9–0.95). Across all victim drugs and drug interaction studies, the mean accuracy of prediction of the fold-increase in victim drug AUC by paroxetine was 89% (range, 76–104%) when nonspecific microsomal binding was considered.

However, failure to consider nonspecific microsomal binding led to a greater than 3-fold underprediction of interaction magnitude (mean accuracy of 29%, range, 22–35%). When alternative estimates of inhibitor concentration (total systemic concentration or unbound maximal concentration at the inlet to the liver, estimated using eq. 5) were used as inputs to the scaling model (with consideration of nonspecific microsomal binding), the overall predictive accuracy did not improve to favor their selection as the estimate of [I]. The mean accuracy was 117% (range, 90–140%) when the estimated unbound maximal concentration at the inlet to the liver was used, and was 127% (range, 97–140%) when the total systemic concentration was used.

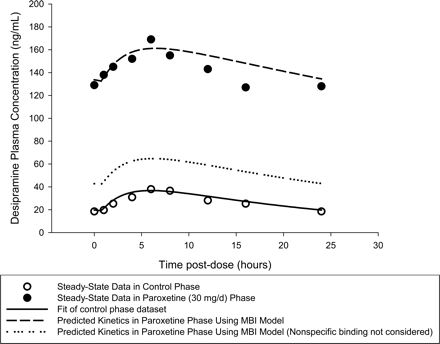
The performance of the scaling model is illustrated in Fig. 2 for the interaction of paroxetine with desipramine (Alderman et al., 1997). For purposes of this exercise, the steady-state pharmacokinetic profile of desipramine (50 mg q.d.) in the control phase (Alderman et al., 1997) was fitted to a one-compartment pharmacokinetic model with an absorption lag time and the following parameters estimated: first-order absorption rate constant (k_a), 0.381 h^-1; absorption lag time (t_lag), 0.79 h; apparent volume of distribution (V/F) 1762 liters; and elimination rate constant (k_el), 0.0408 h^-1. Assuming a hepatic blood flow of 21 ml/min/kg (Davies and Morris, 1993), the impact of CYP2D6 inactivation by paroxetine on the systemic clearance and oral bioavailability of desipramine were estimated from the model-predicted fractional decrement in apparent oral clearance (FDCL_tot 0.81 at a paroxetine dosage of 30 mg q.d.; Table 2), in the context of a well stirred pharmacokinetic model (Wilkinson and Shand, 1975). Assuming that the interaction does not alter volume of distribution [but would alter the apparent volume of distribution (V/F) due to alteration of F] or absorption kinetics, and that changes in systemic clearance will be reflected as changes in desipramine's elimination half-life, the following pharmacokinetic parameters for desipramine post-CYP2D6 inactivation were derived: apparent volume of distribution (V/F), 1122 liters; and elimination rate constant (k_el), 0.0122 h^-1. The corresponding superpositioned steady-state profile is represented in Fig. 2 by a dashed line profile and is in reasonably good agreement with the observed steady-state pharmacokinetic profile (Alderman et al., 1997) of desipramine (50 mg q.d.) with coadministered paroxetine (30 mg q.d. to steady state). In contrast, when nonspecific microsomal binding is not considered in the scaling (FDCL_tot 0.473 at a paroxetine dosage of 30 mg q.d.; Table 2), the resulting pharmacokinetic parameter estimates [apparent volume of distribution (V/F), 1387 liters; and elimination rate constant (k_el), 0.0273 h^-1)] predict a steady-state profile (represented by the dotted line in Fig. 2) that substantially underpredicts the observed interaction, illustrating the importance of nonspecific microsomal binding considerations in quantification of inactivator potency.

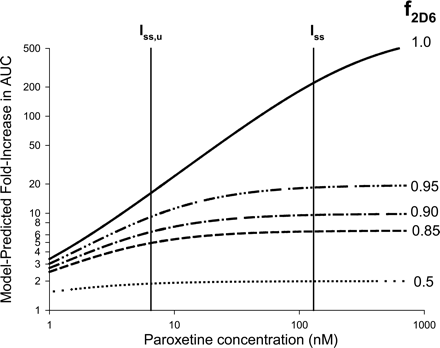
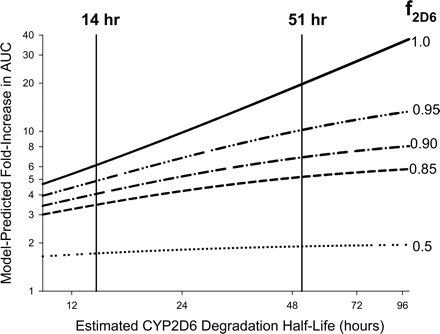
Sensitivity Analyses. Simulations of the sensitivity of the model-predicted fold-increase in victim drug AUC to the estimated enzyme-available inhibitor concentration and CYP2D6 degradation half-life are shown in Figs. 3 and 4, respectively. Sensitivities of the predicted interaction magnitude to both these input parameters were greatest when the victim drug was exclusively cleared by CYP2D6 (f_2D6 ∼1.0). For the victim drugs investigated here (f_2D6 ≤ 0.9), use of steady-state average total plasma paroxetine concentration following 10 mg b.i.d. or 20 to 30 mg q.d. dosing in the various reported paroxetine DDI studies (I_ss in the 80–160 nM range) or corresponding estimates of steady-state maximum portal venous unbound concentration [I_inlet,max,u 17–42 nM using eq. 5 instead of steady-state average unbound concentration (I_ss,u in the 4–8 nM range)] did not significantly alter the predicted magnitude of the drug interaction, since this range of inhibitor exposures (4–160 nM) is outside the dynamic range of the sensitivity curve (Fig. 3). Figure 4 suggests that the use of a 14-h half-life for CYP2D6 [as used for CYP3A4 (Mayhew et al., 2000), based on the half-life of rat CYP3A] instead of the 51-h estimate of human CYP2D6 half-life would result in a 2-fold underprediction of interaction magnitude.

• Download figure
• Open in new tab
• Download powerpoint

Fig. 2.

Prediction of the desipramine-paroxetine interaction by the MBI scaling model. Symbols represent the observed desipramine steady-state plasma concentration-time data before (open circles) and after (filled circles) steady-state coadministration of paroxetine (Alderman et al., 1997). The solid line is the best fit curve for the control desipramine steady-state pharmacokinetic data. The dashed and dotted lines represent the scaling model-predicted profiles following steady-state paroxetine coadministration from in vitro MBI kinetic parameters and the baseline pharmacokinetic parameters of desipramine, with and without consideration of in vitro nonspecific microsomal binding of paroxetine, respectively. Note the underprediction of drug interaction magnitude when in vitro microsomal binding is ignored during scaling.

• Download figure
• Open in new tab
• Download powerpoint

Fig. 3.

Analysis of the sensitivity of the MBI scaling model-predicted drug-drug interaction magnitude (fold-increase in victim drug AUC) to the estimated enzyme-available inhibitor concentration (I) for victim drugs with f_2D6 values ranging from 0.5 to 1.0, using eqs. 2, 3, 4. Note that the sensitivity increases at higher values of f_2D6 and is relatively small when f_2D6 ≤ 0.90, as is the case for all the victim drugs examined in this investigation.

• Download figure
• Open in new tab
• Download powerpoint

Fig. 4.

Analysis of the sensitivity of the MBI scaling model-predicted drug-drug interaction magnitude (fold-increase in victim drug AUC) to the estimated CYP2D6 degradation half-life for victim drugs with f_2D6 values ranging from 0.5 to 1.0, using eqs. 2, 3, 4. Note that the use of a 14-h estimate of CYP2D6 half-life (as opposed to the 51-h estimate) results in an approximately 2-fold underestimation of interaction magnitude for victim drugs examined in this investigation (mean f_2D6 ∼0.87).

Discussion

The predictive utility of a previously described mathematical model for IVIVE of DDIs resulting from MBI (Mayhew et al., 2000) has been demonstrated in this investigation for CYP2D6-inhibitory DDIs involving the selective serotonin reuptake inhibitor antidepressant paroxetine. Across substrates, the accuracy of the model in predicting the magnitude of DDIs was approximately 90%. Thus, it can be inferred that previously published reports of underpredictions of the magnitude of DDIs perpetrated by paroxetine are explained by application of a competitive inhibition model for a mechanism-based enzyme inactivator. Nonlinear accumulation of paroxetine was also predicted by the model with an accuracy greater than 90%, suggesting that autoinactivation of CYP2D6 rather than reversible saturation of the enzyme may largely explain this pharmacokinetic phenomenon.

Nonspecific microsomal binding has been shown to significantly impact the determination of metabolic intrinsic clearance and enzyme kinetic parameters, with its consideration in the prediction of human clearance from in vitro metabolism data reproducibly improving predictive accuracy (Obach, 1997, 1999, 2000; Venkatakrishnan et al., 2000). More recently, it has been demonstrated that nonspecific microsomal binding can account for underestimation of inhibitor potency (i.e., overestimation of IC₅₀ or K_i values) when dealing with lipophilic basic perpetrator drugs (Tran et al., 2002; Margolis and Obach, 2003), with the potential implication being erroneous underestimation of drug interaction risk. The risks of not considering nonspecific microsomal binding in estimating inhibitory potency may be greater when dealing with mechanism-based inactivators, due to the relatively high microsomal concentrations that are typically used during preincubation of the inactivator in these experiments. In this investigation, application of a “total” K_I based on nominal inhibitor concentrations added in vitro resulted in a gross underestimation of the magnitude of drug-drug interactions with several CYP2D6 substrates, in contrast to a 90% accurate prediction on average when an “unbound” K_I estimate was used. When nonspecific binding was not considered, despite application of a MBI model that accounts for time-dependent loss of enzyme activity, a <2-fold increase in victim drug AUC is predicted upon paroxetine coadministration, significantly underestimating the observed 5- to 8-fold magnitudes of clinical interactions of paroxetine with CYP2D6 substrates.

A key assumption of the scaling model used here is that enzyme inactivation is the sole mechanism of these DDIs, since the reversible component of CYP2D6 inhibition by paroxetine is not considered. Furthermore, it is also assumed that the effect of paroxetine is substrate-independent. This is based on the assumption that the MBI completely prevents substrate binding in a productive orientation at the enzyme active site(s), such that metabolic capacity toward all substrates would be equally affected. Atypical kinetics of dextromethorphan metabolism by CYP2D6 have been described (Yu et al., 2001), suggesting that multiple binding orientations are possible. Thus, the theoretical possibility remains that the assumption of substrate independence of K_I and k_inact of mechanism-based inactivation of CYP2D6 by paroxetine may not be true, if the MBI results in an orientation-specific (and hence substrate-dependent) loss of substrate binding at the enzyme active site. Nevertheless, paroxetine reproducibly impairs the clearance of structurally diverse CYP2D6 substrates, which would suggest that the likelihood of paroxetine producing substrate-specific CYP2D6 inhibition is small and of limited clinical relevance.

The lack of information on the in vivo degradation rates of many human drug-metabolizing P450s represents a significant limitation that increases the uncertainty in risk assessment, even when the desired in vitro data are available. In the present investigation, we have utilized an indirect approach of pharmacokinetic deconvolution to estimate the half-life of CYP2D6 in humans as ∼51 h. A comparable mean half-life estimate of 50 h (range 25–80 h) has been reported for human CYP2E1 by measuring the time course of return of chlorzoxazone 6-hydroxylation clearance to baseline following administration of the rapidly cleared CYP2E1 inactivator disulfiram (Emery et al., 1999). Thus, the estimated CYP2D6 half-life of 51 h is in excellent agreement with the degradation half-life estimated for another human P450 isoform within the same family, using a similar indirect approach. When information on enzyme half-life is not available, compound-specific analysis of the sensitivity of the IVIVE model to k_degrad represents a useful approach to estimating the level of confidence in the predicted DDI magnitude. The same is applicable when there is uncertainty in the estimated enzyme-available inhibitor levels due to possible active hepatic uptake (von Moltke et al., 1998) or transient high concentrations during first pass through the liver (Ito et al., 1998; Kanamitsu et al., 2000).

In the current retrospective analysis, the possibility of concentrative hepatic uptake of paroxetine has not been considered due to the lack of data on the extent of hepatocellular uptake of paroxetine, or identified biochemical mechanisms of active hepatic uptake transport of this drug. Paroxetine displays extensive hepatic distribution, with a liver/plasma total concentration ratio of ∼26 (von Moltke et al., 1995). However, it is unknown whether this extent of distribution is significantly in excess of that expected from the relative extents of plasma and hepatic tissue binding. The choice of inhibitor concentration (systemic unbound versus systemic total versus estimated maximum unbound concentration at the inlet to the liver) did not significantly influence the predicted drug interaction magnitudes in the current retrospective analysis because the limits of the range of these alternative exposure estimates following clinical doses of paroxetine were outside the dynamic range of the sensitivity curve for these victim drugs. Thus, a true test of the applicability of I_ss,u of paroxetine as a surrogate of enzyme-available concentrations will require DDI studies using subtherapeutic doses that yield exposures in the dynamic range of the sensitivity curve. The successful prediction of paroxetine DDIs in the current analysis therefore does not necessarily support the general applicability of unbound systemic concentrations of an inhibitor in the prediction of interaction magnitude. Although the application of unbound systemic exposures is theoretically appealing and has been successful for many structurally distinct mechanism-based inactivators (Mayhew et al., 2000; Wang et al., 2004; Ernest et al., 2005), there are many reversible inhibitors for which there is evidence to the contrary. A recent large retrospective analysis points to examples of underprediction of several interactions when this metric of inhibitor concentration was used in the context of a reversible inhibition model, although nonspecific microsomal binding in vitro was not considered in this analysis (Ito et al., 2004). Even after correction for in vitro microsomal binding, and ruling out MBI, Levy and colleagues have shown that the in vivo potencies of fluvoxamine as an inhibitor of CYP1A2 and 2C19 are 10- to 40-fold greater than in vitro estimates (Yao et al., 2001, 2003). Thus, the level of certainty in enzyme-available inhibitor concentrations is a major determinant of the confidence in prospective prediction of DDI magnitude. It is thus recommended that when quantitative predictions of interaction magnitude are made from in vitro data, an analysis of sensitivity to the uncertainty in enzyme-available inhibitor concentrations over the clinical dose/exposure range be performed. When the sensitivity is large, it may be best to express the predicted interaction magnitude as a range derived from a range of estimated [I], weighted by their likelihood inferred from available experimental evidence for the specific perpetrator drug (e.g., information on uptake transport, portal/systemic gradients, etc.).

In summary, the results of the present investigation suggest several important implications for clinical DDI risk assessment from in vitro data when dealing with enzyme inactivators. Mechanism-based inactivation is characterized not only by concentration-dependent, but also time-dependent enzyme inhibition. As a result, risk assessment cannot be performed by a simple comparison of inactivator potency (K_I) against its in vivo exposure. In the case of paroxetine, the I/K_I ratio at the 30 mg q.d. dosing regimen is 0.02, an extremely low value that would typically be suggestive of minimal risk in the context of reversible inhibition. If total plasma concentrations are used, the I/K_I ratio is still only 0.4, a relatively low value that would only be suggestive of medium DDI risk [applying considerations that hold for reversible inhibition (von Moltke et al., 1998; Tucker et al., 2001; Bjornsson et al., 2003; Obach, 2003; Venkatakrishnan et al., 2003)]. Paroxetine, however, produces 5- to 8-fold increases in the exposure of CYP2D6 substrates, observations that are reconciled well by the MBI model, as shown in this investigation. In fact, for a substrate that relies entirely on CYP2D6 (f_2D6 = 1), the model predicts that paroxetine (30 mg q.d.) will produce a 14-fold increase in victim drug AUC. Thus, when MBI is suspect, risk assessment is not straightforward. It requires thorough kinetic analysis and IVIVE using the appropriate scaling model (Mayhew et al., 2000), with consideration of factors such as microsomal binding in vitro, to enable unbiased estimation of inhibitor potency, to ultimately increase confidence in clinical DDI risk assessment from in vitro data.