Abstract
Accurate prediction of the extent of mechanism-based CYP3A inhibition is critical in determining the timing of clinical drug interaction studies in drug development. To evaluate the prediction accuracy of the static and Simcyp time-based approaches, 54 clinical drug interactions involving mechanism-based CYP3A inhibitors were predicted using both methods. The Simcyp time-based approach generated better prediction when 0.03 h−1 was used as the hepatic CYP3A enzyme degradation rate constant (kdeg) value. Of the predictions 87 and 55% had an error less than 2 and 0.5, respectively, relative to the observed values, compared with 57 and 20%, respectively, when the Simcyp default kdeg value of 0.0077 h−1 was used. Accuracy improvement using the kdeg value of 0.03 over 0.0077 h−1 was most evident for trials with observed magnitude of interaction greater than 2-fold; predictions with an error less than 0.5 relative to clinical observations increased from 8 to 48%. For the static approach, 76 and 35% of the predictions had an error less than 2 and 0.5, respectively. Both methods generated good predictions for weak and moderate inhibitors. The prediction accuracy could be affected by our knowledge of disposition of a substrate compound, in vitro inactivation parameter estimates, and the ability of Simcyp to accurately simulate the pharmacokinetics of inhibitors. Nonetheless, both the Simcyp and static approaches are useful tools for assessing the drug-drug interaction potential of a mechanism-based CYP3A inhibitor, especially when human pharmacokinetics of the inhibitor is known and 0.03 h−1 is used as the hepatic CYP3A kdeg value.
Drug-drug interactions remain an area of focus in drug discovery and development. Mechanism-based inhibition of CYP3A is one of the major causes of clinical drug-drug interactions and generally leads to greater concern, as highlighted by the list of moderate and strong CYP3A inhibitors in the Food and Drug Administration (2006) Drug Interaction Guidance. The inhibitory effects of a mechanism-based CYP3A inhibitor persist long after the compound is eliminated from the body because the recovery of CYP3A enzyme activity requires de novo protein synthesis or slow release of the enzyme from the enzyme-inhibitor complex. Because of the primary role of CYP3A in drug disposition, prediction of the clinical drug interaction potential of a mechanism-based CYP3A inhibitor would be helpful in guiding the timing and design of clinical studies.
Several approaches have been developed to predict clinical outcomes of mechanism-based inhibition. The static mathematical model developed by Mayhew et al. (2000) is a commonly used approach to predict mechanism-based drug interactions from in vitro estimated inactivation parameters. Several modifications to the original model have been made to incorporate the effects of intestinal wall metabolism (Wang et al., 2004b), competitive inhibition, and induction (Fahmi et al., 2009). Nonetheless, these static models are only capable of predicting the average magnitude of drug interactions across a population, assuming that the steady state of enzyme inhibition has been reached. Temporal changes in inhibitor concentrations and CYP3A enzyme activities as well as interindividual variability in CYP3A enzyme levels and rate constants of enzyme degradation are not considered. In addition, it is difficult to assess the effects of dosing regimens (e.g., irregular dosing) on the extent of drug interactions using a static model.
Several physiologically based pharmacokinetic models (PBPK) were developed to address some of the aforementioned limitations with static models (Kanamitsu et al., 2000; Zhang et al., 2009; Fenneteau et al., 2010). These PBPK models take into account temporal changes in inhibitor and substrate concentrations and enzyme activities as well as the enzyme inhibition concept in the static models. They can be used to simulate drug concentration-time profiles and to explore the effects of various dosing regimens. Simcyp (Simcyp Limited, Sheffield, UK) is a commercially available absorption, distribution, metabolism, and elimination simulator (Jamei et al., 2009). The Simcyp drug interaction prediction model is a population-based PBPK model. It considers the interplay among demographic, genetic, anatomical, physiological, and drug-specific factors. The objectives of the present study were to evaluate the accuracy of the static and Simcyp time-based models in predicting mechanism-based drug interactions of CYP3A, explore factors that could affect the accuracy of drug interaction predictions, and assess the confidence in drug interaction predictions when human pharmacokinetic data are available.
Materials and Methods
Clinical Drug Interaction Data.
Clinical drug interaction data were collected from PubMed and the University of Washington Drug Interaction Database (http://www.druginteractioninfo.org/). Clinical drug interaction studies involving seven mechanism-based CYP3A inhibitors and eight substrates were chosen based on available inhibitor and substrate profiles in Simcyp.
Simcyp Simulations.
Time-based simulations were performed using the Simcyp Population-based ADME Simulator (version 8.2, SP2, version 9.0, or version 9.10) according to the trial design described in the publication including the same number of subjects, age range, gender ratio, and dosing regimen. For studies conducted in Japan, a Sim-Japanese population was used. For studies conducted in Egypt, the United States, or Europe, a Sim-Healthy Volunteer population was used. Ten trials were simulated for each inhibitor-substrate pair.
Input parameters were default values supplied by the program unless otherwise stated. The clarithromycin profile was built using the parameters listed in Table 1. To simulate plasma concentration-time profiles for sustained-release (SR) formulations of verapamil or diltiazem, each dose, as indicated in Table 2, was divided into 10 equal minidoses administered at fixed intervals on 10 consecutive occasions. For each divided minidose, the simulation was run using the first-order absorption model and one-compartment distribution model. In addition, for the diltiazem SR formulation, the values of systemic clearance and volume of distribution of diltiazem were changed to 48.3 l/h with a coefficient of variation (CV) value of 27% and 5.2 l/kg with a CV value of 27.2%, respectively (Ochs and Knüchel, 1984) to simulate the observed diltiazem plasma profile (Robbins-Weilert et al., 1999). In vitro mechanism-based inactivation parameters were added to the interaction profiles of saquinavir, ritonavir, and fluoxetine (Table 3) when simulations were performed using 0.03 h−1 as the kdeg value for hepatic CYP3As. Microsomal protein bindings were predicted using the quantitative structure-activity relationship model (Turner et al., 2006).
Model parameters used in clarithromycin simulation
Summary of the 54 clinical studies and predictions based on Simcyp time-based model and static model
Values highlighted in bold had an absolute difference between the predicted and observed AUC changes >2.
Key inhibitor parameters provided in the Simcyp program
Static Prediction Model.
The extent of drug interactions was predicted using the eq. 1 that incorporates the effects of competitive inhibition and mechanism-based inhibition in both the intestine and liver (Fahmi et al., 2008):
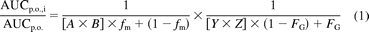where AUCp.o., i and AUCp.o. are the areas under the curve of an affected substrate in the presence and absence of an inhibitor, respectively, FG is the intestinal bioavailability of the substrate, and fm is the fraction of the substrate metabolized by CYP3A in the liver. A and Y are the mechanism-based inhibition components in the liver and intestine, respectively; B and Z are the competitive inhibition components in the liver and intestine, respectively. They can be expressed as (eqs. 2 and 3):
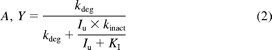and
where kinact represents the maximal inactivation rate constant, KI represents the inhibitor concentration when the rate of inactivation reaches half of the maximal value, and kdeg represents the rate constant of enzyme degradation. The mean kdeg value of 0.03 h−1 was used for both hepatic and intestinal CYP3As in the static model; 0.03 h−1 was the default kdeg value for intestinal CYP3As in Simcyp. Iu represents the unbound inhibitor concentration in the liver or intestine. The inhibitor concentration in the liver was assumed to be equal to the average systemic plasma concentration of the inhibitor calculated from observed AUCτ divided by τ, where τ represents the dosing interval (Table 4). When the observed AUCτ was not available, Simcyp-simulated AUCτ was used to calculate the average plasma concentration. The inhibitor concentration in the intestine was calculated from eq. 4 (Fahmi et al., 2008),
where Dose is total daily dose of an inhibitor given orally, ka represents first-order absorption rate constant, fa represents the fraction of the dose absorbed, QG is the intestinal (villous) blood flow (17.9 l/h) (Yang et al., 2007), and Freq is the frequency of daily dose. Unbound inhibitor concentration in the intestine was assumed to be equal to IG.
Comparison of Simcyp-simulated inhibitor concentrations with clinical observations
Absorption rate constants, unbound fractions in plasma (fu, p) and microsomes (fu, mic), mechanism-based inactivation parameters, and competitive inhibition constants of the inhibitors used in the static model were the same as those in the Simcyp program (Table 3). Fraction absorbed (fa) was assumed to be 1 for inhibitors other than clarithromycin (Table 1). Intestinal bioavailabilities (FG) of the substrates, which were the same as those in the Simcyp, were 0.57, 0.75, 0.66, 0.78, 0.99, 0.56, and 0.96 for midazolam, triazolam, simvastatin, nifedipine, alprazolam, sildenafil, and zolpidem, respectively. The fraction of the dose metabolized by hepatic CYP3As (fm) was assumed to be 0.9 for midazolam, triazolam, simvastatin, nifedipine, alprazolam, and sildenafil and 0.48 for zolpidem (Farkas et al., 2009). When competitive inhibition was not considered in the prediction, B and Z in eq. 1 were equal to 1.
Data Analysis.
The simulated mean AUC ratios or geometric mean AUC ratios of a substrate in the presence and absence of an inhibitor were compared with the corresponding AUC ratios observed from clinical studies. Prediction error was calculated from the absolute difference between the predicted and observed AUC ratios. In addition, the predicted mean or geometric mean values of AUC and Cmax values of a substrate or an inhibitor were compared with those published values.
The average deviation (AD) of the predicted AUC ratio from the observed AUC ratio (eq. 5) was used to measure the prediction bias of different methods. A smaller absolute value of average deviation indicates a smaller prediction bias. The geometric mean-fold error (GMFE) (eq. 6) was calculated for readers' convenience. The root mean square error (RMSE) (eq. 7) was calculated to measure the precision of these methods. A smaller root mean square error indicates greater precision.
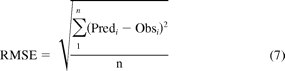where Predi represents the predicted AUC ratio, Obsi represents the observed AUC ratio of the ith drug interaction trial, and n is the total trial number in each category.
Results
Thirty-two clinical studies involving 54 inhibitor-substrate pairs were included in this analysis (Table 2). These clinical studies included trials investigating the effects of doses, duration of pretreatment, and the CYP3A recovery process on the extent of mechanism-based inhibition. The inhibitors included strong inhibitors such as clarithromycin, ritonavir, and saquinavir; moderate inhibitors such as erythromycin, diltiazem, and verapamil; and weak inhibitors such as fluoxetine. The affected substrates included sensitive CYP3A substrates such as midazolam, simvastatin, triazolam, sildenafil, and nifedipine; a substrate having low extraction ratio (i.e., alprazolam); and a substrate only partially metabolized by CYP3A (i.e., zolpidem). In addition, data from both intravenous and oral administration of midazolam were included in this analysis. For verapamil and diltiazem, both immediate-release (IR) and SR formulations were included.
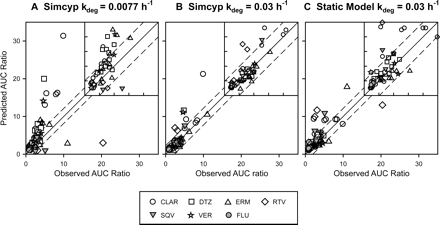
To evaluate the accuracy of Simcyp in predicting drug interactions for mechanism-based CYP3A inhibitors, drug interaction trials were first simulated using the default values provided by Simcyp. Figure 1A and Table 2 show that the majority of drug interactions were overpredicted, except that the extent of drug interactions of saquinavir and ritonavir was underpredicted, which probably occurred because the mechanism-based inactivation for these two compounds was not considered by the program. Overall, 57% of the predictions had an error (i.e., absolute difference between the predicted and observed values) less than 2 relative to clinical observations, and 20% of the predictions had an error less than 0.5. Predictions with an error less than 0.5 were significantly reduced when only the trials with observed AUC ratios greater than 2-fold were considered (Table 6).
Comparisons of the Simcyp time-based approach (A and B) and the static model (C) to predict mean AUC ratios of clinical drug interactions from 54 inhibitor-substrate pairs. The points represent the observed mean (or geometric mean) AUC change versus predicted AUC change for each inhibitor-substrate pair. The solid line represents the unity, and the dotted lines represent a prediction error (= |predicted AUC ratio − observed AUC ratio|) of 2 relative to observed values. Insets are the enlarged areas between 0 and 10. CLAR, clarithromycin; DTZ, diltiazem; ERM, erythromycin; RTV, ritonavir; SQV, saquinavir; VER, verapamil; FLU, fluoxetine.
Hepatic CYP3A Degradation Rate Constant.
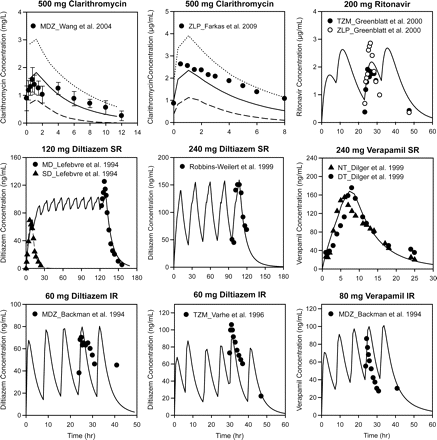
The default kdeg value for both hepatic CYP3A4 and CYP3A5 in the Simcyp model is 0.0077 h−1, corresponding to a half-life of 90 h. A recent study investigated the effects of age and sex on the time course of CYP3A recovery after multiple-dose clarithromycin administration using intravenous and oral midazolam as probe substrates. The results showed that the mean kdeg value for hepatic CYP3A in the population studied was approximately 0.03 h−1 (Wang et al., 2004a), corresponding to a half-life of 23 h. To examine whether Simcyp could reproduce the results from this study when 0.03 h−1 was used as the kdeg value, the clinical study was simulated using the same study design in the Sim-Healthy Volunteer population. The predicted magnitudes of clarithromycin-midazolam interactions for both intravenous and oral midazolam were in good agreement with the observed values when a kdeg value of 0.03 h−1 were used (Table 2). In contrast, significant overpredictions were observed when a kdeg value of 0.0077 h−1 were used. Figure 2 and Table 4 show that the simulated plasma concentration profile and pharmacokinetic parameters of clarithromycin were comparable with those observed in the clinical study (Wang et al., 2004a).
Comparison between simulated and observed plasma concentration profiles of inhibitors. Symbols represent the mean observed plasma concentrations. Solid lines represent the mean simulated plasma concentrations, dashed lines represent the 5th percentile, and dotted lines represent the 95th percentile. Error bars represent S.D. The dosages and formulations of the inhibitors are provided in the graph titles, and figure legends provide the source of the observed data points. MDZ, midazolam; ZLP, zolpidem; TZM, triazolam; MD, multiple-dose; SD, single-dose; NT, nighttime; DT, daytime.
To examine whether using a kdeg value of 0.03 h−1 could improve the prediction accuracy of the Simcyp time-based approach, default kdeg values for both hepatic CYP3A4 and CYP3A5 in the program were replaced with 0.03 h−1 while the CVs were maintained at 68%. In addition, mechanism-based inhibition parameters were added to the interaction profiles of saquinavir, ritonavir, and fluoxetine (Table 3). Compared with the default kdeg values, using kdeg values of 0.03 h−1 significantly improved the prediction accuracy (Fig. 1B; Table 2). Approximately 90% of the predictions had an error less than 2 relative to the observed values, and the predictions with an error less than 0.5 were approximately 54%, which represented more than a 2-fold improvement over those generated using the default kdeg values. These improvements to the prediction accuracy were most evident when only the trials with observed AUC ratio greater than 2-fold were considered (Table 6).
The Static Prediction Model.
The Simcyp time-based approach used in the aforementioned studies considered the effects of both competitive inhibition and mechanism-based inhibition. To make a valid comparison of the Simcyp time-based approach and the static approach, the static model (eq. 1) combined with the competitive inhibition components and gut first-pass effect was used. Parameters used in this prediction are detailed under Materials and Methods. Approximately 76% of the predictions had an error less than 2 compared with the observed values, and approximately 35% of the predictions had an error less than 0.5 (Fig. 1C; Table 2). Similar prediction accuracy was obtained when only the trials with observed AUC ratio greater than 2-fold were considered (Table 6). Significant overpredictions of the magnitude of interaction were observed with strong CYP3A inhibitors such as ritonavir, saquinavir, and clarithromycin (Table 2). Prediction results were the same as those shown in Table 2 when the static model in eq. 1 without the competitive inhibition components was used.
Inhibitor and Substrate Concentration Profiles.
To explore factors that could affect the prediction accuracy of the Simcyp approach, simulated inhibitors and substrate concentration profiles were compared with those observed in clinical studies. Plasma concentration-time profiles for inhibitors were simulated using a first-order absorption model and a one-compartment distribution model with the default parameters provided by the program unless otherwise specified. Figure 2 shows the mean plasma concentration-time profiles of the inhibitors. The AUC and Cmax values of these inhibitors are summarized in Table 4. The simulated and observed profiles were generally comparable with the exception of those for verapamil IR and diltiazem IR (Fig. 2). Simcyp overpredicted the AUC value of verapamil in the verapamil IR-simvastatin study and underpredicted the AUC and Cmax values of fluoxetine and saquinavir (Table 4).
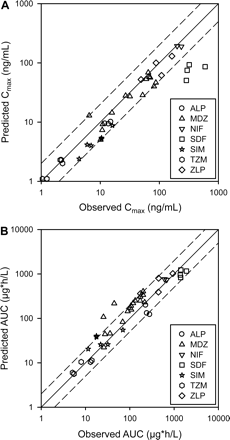
The observed and predicted mean plasma concentration profiles of substrates at the baseline are shown in Fig. 3 and Supplemental Fig. 1. The observed and predicted AUC and Cmax values of these substrates were generally comparable (Fig. 4); 92% of the predicted Cmax and 87% of the predicted AUC values fell within 2-fold of the observed values, similar to a previous report (Einolf, 2007). Several significant deviations in the observed and predicted pharmacokinetic values were observed. Mean midazolam AUC in the verapamil SR-midazolam IV study was overpredicted by 5-fold compared with the clinical observation, but its predicted clearance was similar to the observed clearance (data not shown). The predicted Cmax values of sildenafil were approximately 3- to 7-fold lower than the observed values. In addition, the predicted AUC values of alprazolam were approximately 2-fold lower than the observed values, and the predicted plasma profiles of alprazolam deviated from those observed when the intrinsic clearance of alprazolam was estimated using recombinant CYP3As (version 9.0) instead of human liver microsomes (version 8.2) (Fig. 3). The predicted profiles of triazolam and nifedipine generally agreed with the observed profiles, but most of the predicted plasma profiles of sildenafil and simvastatin deviated from the observed profiles (Fig. 3; Supplemental Fig. 1).
Comparison between predicted and observed plasma concentration profiles for substrates at the baseline. Symbols represent the mean observed plasma concentrations of a substrate, manually adapted from the publication noted in the graph titles. The inhibitor-substrate pair is shown in the symbol legend. Unless otherwise noted in the symbol legend, solid lines represent the mean predicted plasma concentrations of a substrate, dashed lines represent the 5th percentile, and dotted lines represent the 95th percentile. RTV, ritonavir; ALP, alprazolam; CLAR, clarithromycin; MDZ, midazolam; DTZ, diltiazem; SIM, simvastatin; SDF, sildenafil; NIF, nifedipine; VER, verapamil; TZM, triazolam; ZLP, zolpidem.
Predicted and observed pharmacokinetic parameters Cmax (A) and AUC (B) for substrates obtained from the control groups of the clinical trials (n = 42). The solid line represents the unity, and the dotted line represents a 2-fold deviation from the unity. ALP, alprazolam; MDZ, midazolam; NIF, nifedipine; SDF, sildenafil; SIM, simvastatin; TZM, triazolam; ZLP, zolpidem.
In Vitro Inactivation Parameters.
The inactivation parameters kinact and KI represent two of the six important factors in the prediction models that may affect the prediction accuracy because they are sensitive to the in vitro study design (Yang et al., 2005). The effects of inactivation parameters generated from different laboratories on the prediction accuracy were examined (Table 5). For verapamil and diltiazem, the predicted magnitude of AUC changes was comparable with the observed data despite the different parameter estimates. For clarithromycin, there were large differences in KI estimates. However, incorporating fu, mic values minimized the differences in the KI estimates and resulted in similar predictions, which underscores the importance of considering the nonspecific microsomal binding in drug interaction predictions. For erythromycin, large differences in the kinact and KI estimates resulted in a significant difference in the predicted extent of interactions. In most cases, clinical drug interactions were predicted using these in vitro kinact and KI estimates.
Summary of drug interaction predictions using inactivation parameter estimates from various sources
Predictions were performed using Simcyp version 9.10.
Summary of Predictions Using Different Models.
To assess the confidence in the different prediction approaches, the prediction accuracy in various categories is summarized in Table 6. The static model generated more accurate predictions for weak and moderate CYP3A inhibitors. The Simcyp time-based approach yielded the most accurate predictions when the kdeg value of 0.03 h−1 was used. Greater than 90% of the predictions had an error less than 2 relative to the observed AUC ratios for trials using midazolam as a probe substrate and trials with moderate CYP3A inhibitors. For trials with an observed AUC ratio less than 2-fold including trials with weak inhibitors and trials with the substrate only partially metabolized by CYP3A (i.e., zolpidem), approximately 90% of the predictions had an error less than 1, despite the fact that some of the predicted substrate or inhibitor plasma profiles deviated from those observed (Figs. 2 and 3; Supplemental Fig. 1). For trials with strong inhibitors, the prediction accuracy mostly depended on how well Simcyp predicted the substrate profiles whereas overprediction of inhibitor concentrations such as ritonavir and saquinavir seemed less critical probably because maximal CYP3A inhibition was achieved at lower concentrations (Tables 2 and 4; Figs. 2 and 3). For trials with moderate inhibitors, the prediction accuracy primarily depended on adequate simulation of substrate and inhibitor profiles, e.g., similar AUC and Cmax, and overlapping profiles of observed and simulated plasma inhibitor concentrations (Tables 2 and 4; Fig. 2).
Summary of prediction accuracy of different models
Discussion
Several retrospective analyses were conducted to compare the prediction accuracy of the Simcyp models with that of static models (Einolf, 2007; Fahmi et al., 2009). However, only a small portion of the entire dataset in these studies involved mechanism-based inhibitors of CYP3A. In some cases, different kdeg values were used for hepatic CYP3A when the accuracy among prediction models was compared. As a result, it is difficult to evaluate the accuracy of Simcyp in predicting mechanism-based inhibitions from these studies. The present study examined the prediction accuracy of Simcyp as an out-of-box application, compared with those of the static and Simcyp time-based models using 0.03 h−1 as the kdeg value for hepatic CYP3A. In addition, factors that affect prediction accuracy of these two models were examined, which could help to determine the confidence in drug interaction predictions and enable informed decision-making.
The kdeg value of hepatic CYP3A is one of the important factors that affect the accuracy of mechanism-based drug interaction predictions. However, this parameter cannot be directly measured in human subjects. Various in vitro and in vivo approaches have been used to estimate the kdeg value of hepatic CYP3A (Yang et al., 2008). The mean values estimated from these studies range from 0.007 to 0.02 h−1, and no consensus has been reached on the appropriate kdeg value for hepatic CYP3A. A recent clinical study was conducted to examine the time course of CYP3A activity recovery after multiple doses of clarithromycin using intravenous and oral midazolam as probe substrates (Wang et al., 2004a). By fitting the ratios of midazolam hepatic intrinsic clearance to a mechanism-based enzyme inactivation model, the mean kdeg value estimated from this study was approximately 0.03 h−1. The present study showed that predictions conducted using both the static and Simcyp models with the kdeg value of 0.03 h−1 were in excellent agreement with clinical observations from the studies that investigated the time course of inhibitory effects of CYP3A inhibitors such as clarithromycin, erythromycin, and diltiazem (Table 2). Predictions generated with the kdeg value of 0.03 h−1 were more accurate and less biased than those generated with 0.0077 h−1. In fact, when studies with observed AUC changes less than 2-fold were excluded, predictions using the kdeg value of 0.03 h−1 were approximately 2 to 6 times better than those generated with 0.0077 h−1 (Table 6). In addition, the kdeg value of 0.03 h−1 also generated better prediction accuracy compared with the kdeg values used by Fahmi et al. (2009) and Xu et al. (2009) when the common data from these studies were compared. Taken together, these findings suggest that using 0.03 h−1 as the mean kdeg value for hepatic CYP3A generates better predictions for drug interactions involving mechanism-based CYP3A inhibitors.
Simcyp-simulated results were comparable to those generated with other PBPK models (Zhang et al., 2009; Fenneteau et al., 2010). For midazolam drug interaction studies, greater than 90% of the predictions had an error less than 2; more accurate predictions were achieved when the observed and simulated profiles were superimposed (e.g., diltiazem SR and verapamil SR). These data suggest that the Simcyp approach can be useful in predicting the extent of midazolam interactions for an investigational new drug that has a mechanism-based CYP3A inhibition potential. In addition, interindividual variability of drug interactions could also be assessed; the predicted ranges of AUC changes were comparable with the actual ranges observed in clinical studies (Table 5).
Several drug interactions were overpredicted by Simcyp when the kdeg value of 0.03 h−1 was used, which were probably due to the deviation of the predicted substrate profiles from those observed. For example, the design of the clarithromycin-midazolam study (Gurley et al., 2008) was similar to those of two other clarithromycin-midazolam studies (Table 2), but the observed extent of interactions among these studies differed by nearly 3-fold. Predicted mean baseline midazolam concentrations were lower compared with those observed (Fig. 3), indicating that additional information is needed for Simcyp to capture the interindividual variability in this study. In the case of the ritonavir-alprazolam interaction, when the alprazolam plasma profile was predicted using the intrinsic clearance estimated from human liver microsomes, the predicted magnitude of interactions was reduced to 4.4-fold. Consequently, the prediction error was less than 2. The above examples show the importance of accurately predicting substrate profiles, especially for moderate and strong inhibitors. Reasons for the poor predictions of simvastatin or sildenafil interaction studies need further investigation.
In the current version of Simcyp, the first-order absorption model is the only absorption model available for inhibitors. To simulate plasma concentration profiles of diltiazem SR and verapamil SR, the daily doses need to be given in 10 equally divided minidoses consecutively at 10 fixed dosing intervals. This approach was proved to be valid because the simulated profiles and pharmacokinetic parameter estimates were comparable to those observed (Fig. 2; Table 4). In the present study, inhibitor concentration profiles were simulated using pharmacokinetic parameters obtained from clinical studies, assuming first-order absorption and one-compartment distribution; nonlinear pharmacokinetic properties such as autoinhibition and metabolite interaction were not considered. Nonetheless, the simulated profiles of the inhibitors reported in this study were generally comparable with those observed. This finding may be attributed to several factors. For example, although metabolites of several inhibitors are potent CYP3A inhibitors (Mayhew et al., 2000; Wang et al., 2004b; Zhao et al., 2007), the parent compounds have to be metabolized first to inactivate the enzyme; therefore, it is difficult to distinguish whether the parent compounds or their metabolites are responsible for CYP3A inactivation. In addition, for most inhibitors used in this study, the effect of autoinhibition may not be significant at the doses studied and could sometimes be dealt with by applying a large coefficient of variation of the clearance parameter (e.g., ritonavir). As with most other methods, prediction accuracy of Simcyp for a potential victim of mechanism-based inhibition may be limited by our knowledge of the disposition of the victim compound. In addition, Simcyp has limited ability to simulate the plasma concentration profiles of potential inhibitors with target-mediated saturable distribution kinetics (data not shown).
For a potential mechanism-based inhibitor, if the plasma concentration profile of the inhibitor or its victim cannot be confidently simulated or predicted by Simcyp, the static model may be used as an alternative approach to predict the extent of interaction. For an inhibitor whose human plasma profiles can be simulated using Simcyp, prediction using the static model may be used to categorize the inhibitor and assess confidence in the Simcyp prediction. Approximately 90% of predictions generated using the static model had an error less than 2 for weak and moderate inhibitors, which were comparable with the predictions generated using the Simcyp time-based approach with a kdeg value of 0.03 h−1. The Simcyp approach was more accurate than the static model when predictions with an error less than 0.5 and 1 were predicted, which may be more relevant for weak and moderate inhibitors. For the static approach, the majority of the inaccuracies occurred when drug interactions involving strong CYP3A inhibitors were predicted, probably because inhibitor concentrations lower than the input values were sufficient to exhibit maximal inactivation of CYP3A, highlighting the importance of considering the temporal changes in active enzyme levels in the body. It is worth noting that unbound average inhibitor concentrations at steady state were used as the input values in the static model. When unbound maximal inhibitor concentrations were used, the overall prediction accuracy was reduced to 61 from 76% (data not shown). In addition, prediction results were the same for this dataset irrespective of whether the competitive inhibition components in eq. 1 were considered or not.
The cutoffs for prediction errors were arbitrary, and the prediction accuracy summarized from this study varied slightly when simulations were performed in different in silico populations or with different parameters. Sometimes, the predicted AUC ratios were comparable with those observed even though the simulated substrate plasma profiles deviated from clinical observations (e.g., sildenafil); therefore, the prediction results should be interpreted with caution. No matter which method is used, there are uncertainties about factors that determine the prediction accuracy such as the in vitro estimated inactivation parameters. For example, there is large variability in reported kinact and KI estimates for erythromycin. The observed inconsistencies in the predicted AUC changes may be due to variability in enzyme sources, differences in experimentally measured versus model-predicted nonspecific protein binding, and/or the physiochemical properties of erythromycin.
In conclusion, the results from this study suggest that Simcyp provides good prediction of the magnitude of drug interactions with mechanism-based CYP3A inhibitors when human pharmacokinetics of a substrate can be adequately predicted, the inhibitor profile can be simulated from human pharmacokinetic data, and a hepatic kdeg value of 0.03 h−1 is used. The static model is also a useful tool for weak and moderate inhibitors with known human pharmacokinetics. The prediction accuracy summarized in this study may be applied to situations for which human pharmacokinetics of a potential inhibitor or substrate is unknown, but there is adequate confidence in the predicted concentrations.
Acknowledgments.
I thank Amy O. Johnson-Levonas and Kathleen Newcomb (Merck Research Laboratories) for help in preparing this article for publication, Regina Wang for contributing inactivation parameters of the mechanism-based inhibitors, and Drs. Charlie Thompson, Christopher Gibson, and Deborah Nicoll-Griffith for reading this article and for helpful suggestions.
Footnotes
Article, publication date, and citation information can be found at http://dmd.aspetjournals.org.
doi:10.1124/dmd.110.032177.
↵
The online version of this article (available at http://dmd.aspetjournals.org) contains supplemental material.-
ABBREVIATIONS:
- PBPK
- physiologically based pharmacokinetics
- SR
- sustained-release formulation
- CV
- coefficient of variation
- AUC
- area under the concentration-time curve
- IR
- immediate-release formulation
- GMFE
- geometric mean-fold error
- RMSE
- root mean square error.
- Received January 12, 2010.
- Accepted April 2, 2010.
- Copyright © 2010 by The American Society for Pharmacology and Experimental Therapeutics
