Abstract
With efforts to reduce cytochrome P450-mediated clearance (CL) during the early stages of drug discovery, transporter-mediated CL mechanisms are becoming more prevalent. However, the prediction of plasma concentration-time profiles for such compounds using physiologically based pharmacokinetic (PBPK) modeling is far less established in comparison with that for compounds with passively mediated pharmacokinetics (PK). In this study, we have assessed the predictability of human PK for seven organic anion-transporting polypeptide (OATP) substrates (pravastatin, cerivastatin, bosentan, fluvastatin, rosuvastatin, valsartan, and repaglinide) for which clinical intravenous data were available. In vitro data generated from the sandwich culture human hepatocyte system were simultaneously fit to estimate parameters describing both uptake and biliary efflux. Use of scaled active uptake, passive distribution, and biliary efflux parameters as inputs into a PBPK model resulted in the overprediction of exposure for all seven drugs investigated, with the exception of pravastatin. Therefore, fitting of in vivo data for each individual drug in the dataset was performed to establish empirical scaling factors to accurately capture their plasma concentration-time profiles. Overall, active uptake and biliary efflux were under- and overpredicted, leading to average empirical scaling factors of 58 and 0.061, respectively; passive diffusion required no scaling factor. This study illustrates the mechanistic and model-driven application of in vitro uptake and efflux data for human PK prediction for OATP substrates. A particular advantage is the ability to capture the multiphasic plasma concentration-time profiles for such compounds using only preclinical data. A prediction strategy for novel OATP substrates is discussed.
Introduction
The prediction of human pharmacokinetics (PK) is pivotal to aid in the selection of new molecular entities with appropriate PK properties for clinical development. Physiologically based pharmacokinetic (PBPK) models have long provided a mechanistic framework for improved understanding and predictions of in vivo PK (Bischoff, 1975; Kawai et al., 1998). Successful predictions of human PK have been demonstrated using relevant in vitro and physicochemical data within such models (Jones et al., 2006; De Buck et al., 2007; Rostami-Hodjegan and Tucker, 2007; Jones et al., 2011). This approach has proven particularly successful for highly permeable compounds for which metabolism is the predominant clearance (CL) mechanism, with negligible contribution of transporters to the overall disposition of these molecules (biopharmaceutics drug disposition classification system classes 1 and 2) (Wu and Benet, 2005). It should be emphasized that for these types of compounds, at equilibrium, the intracellular free drug concentration is expected to be equal to the free plasma concentration in the absence of CL from the tissue; therefore, the key PBPK model assumptions of flow-mediated distribution and well-stirred kinetics are valid. With efforts to reduce cytochrome P450-mediated CL during drug discovery by reducing lipophilicity and increasing polarity, transporter-mediated PK is becoming more prevalent, particularly as the focus of drug discovery is moving away from the typical aminergic G protein-coupled receptors and enzyme targets to ion channels and peptidic receptors. For these more poorly permeable compounds (biopharmaceutics drug disposition classification system classes 3 and 4) (Wu and Benet, 2005), liver transporters may become an important determinant of disposition. The use of generic PBPK models therefore becomes limited, because hepatic uptake will lead to significant differences between the free concentrations in the hepatocyte and plasma.
A number of recent studies provide evidence that compounds with poorly predicted PK are often substrates for transporters (Soars et al., 2009; Watanabe et al., 2010). Improvement in PK prediction for such compounds requires accurate estimation of the extent of active uptake and/or efflux in the hepatocyte. The movement of a compound across the hepatocyte cell membrane is modulated via passive diffusion and active transport, such as active uptake via organic anion-transporting polypeptides (OATPs). Once in the hepatocyte, substrates may be metabolized via cytochrome P450-mediated metabolism or excreted into the bile via efflux transporters, e.g., multidrug resistance protein 2 or breast cancer resistance protein. This has resulted in the development of a number of in vitro assays with varying complexity that allow assessment of these processes either in isolation or combination (Giacomini et al., 2010). These include suspended hepatocytes (Kitamura et al., 2008; Paine et al., 2008), plated hepatocytes (Poirier et al., 2008; Yabe et al., 2011), sandwich cultured hepatocytes (Lee et al., 2010; Yan et al., 2011), and a range of transfected cell lines expressing individual transporters (Yamashiro et al., 2006; Kitamura et al., 2008).
The sandwich culture human hepatocyte system (SCHH) involves culturing hepatocytes in a sandwich format between collagen and Matrigel to allow polarization of the cells (Liu et al., 1999; Bi et al., 2006; Lee et al., 2010). Through modulation of calcium ions, this in vitro system can be used to assess both uptake and biliary efflux (Liu et al., 1999; Bi et al., 2006). Simultaneous assessment of all the processes occurring in SCHH and mechanistic application of the data generated are currently lacking.
Mechanistic models have been used to describe in vitro uptake in suspended and plated hepatocytes (Paine et al., 2008; Poirier et al., 2008). Such in vitro data have been integrated either into semimechanistic or whole-body PBPK models to simulate in vivo PK for OATP substrates in rats (Paine et al., 2008; Poirier et al., 2009a,b; Watanabe et al., 2009) and humans (Poirier et al., 2009a; Watanabe et al., 2009). In most cases, successful predictions were only achieved when empirical scaling factors were incorporated.
The aim of this work was to examine the predictability of transporter-mediated PK in humans using seven OATP substrates, selected on the basis of the availability of clinical intravenous data. The SCHH assay was optimized to allow investigation of active/passive uptake and biliary efflux in the same hepatocyte donor and under the same experimental conditions. For each compound, in vitro SCHH data were simultaneously modeled to generate in vitro parameter estimates. In conjunction with other in vitro and physicochemical properties, these parameters were then incorporated into a whole-body PBPK model to assess the predictability of the clinical PK. A scaling approach is proposed, and its potential application to novel compounds is discussed.
Materials and Methods
Materials.
Compounds were purchased from Sequoia Research Products (Pangbourne, UK). HT media, CP media, HI media, and torpedo antibiotic mix were purchased from Celsis IVT (Baltimore, MD). Matrigel was purchased from BD Biosciences (Woburn, MA). Hanks' balanced salt solution (HBSS) was purchased from Invitrogen (Carlsbad, CA). All other chemicals were purchased from Sigma-Aldrich (St. Louis, MO).
Compound Selection.
Seven compounds were investigated, namely, pravastatin, cerivastatin, bosentan, fluvastatin, rosuvastatin, valsartan, and repaglinide. Compound selection was based on the availability of clinical intravenous data. Corresponding in vitro and physicochemical data were generated in-house for these compounds using standard assays that have been described elsewhere in the literature (Allan et al., 2008).
SCHH Experimental Procedure.
Cryopreserved human hepatocytes from donors HU4168, RTM, and BD109 were purchased from CellzDirect (Pittsboro, NC), Celsis IVT, and BD Biosciences, respectively. These lots were characterized previously in-house and are known to have functional transport activity. The hepatocytes were cultured in a sandwich format as reported previously (Bi et al., 2006; Li et al., 2010).
In brief, the cryopreserved hepatocytes were thawed in completed HT medium (thawing medium) and spun down at 50g for 3 min. The excess medium was removed, and the hepatocyte pellet was resuspended to 7.0 × 105 cells/ml in completed CP medium (plating medium). The hepatocyte suspension was then seeded onto 24-well BioCoat collagen I plates at 0.5 ml/well, and cells were allowed to attach overnight in a humidified incubator at 37°C with 5% CO2. On day 2, the excess hepatocytes were removed, and the wells were washed with completed HI culture medium (incubation medium) at room temperature. Each well was then overlaid with Matrigel at a concentration of 0.25 mg/ml in ice-cold completed HI medium. Media were replaced with completed HI medium daily until the day of the experiment.
On day 5, cells were washed twice and preincubated for 10 min at 37°C in either 1) HBSS buffer containing 0.1 mM rifamycin SV (inhibits a range of transporters) (Vavricka et al., 2002), 2) HBSS buffer, or 3) Ca2+/Mg2+-free HBSS containing 1 mM EGTA. Incubations were performed in two donors (except for bosentan) and on a number of occasions. Substrates dissolved in the relevant condition buffer were added at 1 or 2 μM and incubated at 37°C over 0.5 to 30 min; a minimum of three time points were taken in duplicate for each condition. Rosuvastatin was used as a positive control in all experiments. The cells were lysed with 0.5 ml of methanol containing internal standard at room temperature for 20 min at 150 rpm. The samples were transferred to a 96-deep well plate and evaporated under 40°C gaseous N2. The residue was reconstituted in 70% methanol and analyzed using liquid chromatography-tandem mass spectrometry. Parallel wells of hepatocytes were lysed with radioimmunoprecipitation assay buffer (TEKnova, Hollister, CA) or M-PER Mammalian Protein Extraction Reagent (Thermo Fisher Scientific, Waltham, MA) for protein quantification by a BCA Protein Assay Kit-Reducing Agent Compatible (Thermo Fisher Scientific). Protein amounts were determined from the difference between the protein amount for each hepatocyte donor and the protein amount in blank wells containing Matrigel alone.
Bioanalysis Procedure.
Analysis of 20-μl samples was performed using high-performance liquid chromatography (G1310 1100 series isocratic pump; Hewlett Packard, Palo Alto, CA) followed by tandem mass spectrometry (API 4000; MDS Sciex, Concord, ON, Canada) using a 2-min run time per sample. The mobile phase used to load the column (Dash HTS Hypersil Gold, 20 × 2.1 mm; 5 μm) was 2 mM ammonium acetate in 90% methanol containing 0.027% formic acid (v/v); elution was performed at 0.7 min using a mobile phase of 2 mM ammonium acetate in 10% methanol containing 0.027% formic acid (v/v). The flow rate was set at 1 ml/min. The mass/charge ratio (m/z) and collision energies (electron volts) for each compound were as follows: pravastatin m/z 423 → 101, −40 eV; cerivastatin m/z 460 → 356, 50 eV; bosentan m/z 552 → 202, 40 eV; fluvastatin m/z 412 → 266, 25 eV, rosuvastatin m/z 480 → 418, −25 eV, valsartan m/z 434 → 350, −25 eV, and repaglinide m/z 453 → 230, 25 eV. The internal standard used in all analyses was an in-house compound ((2E)-3-(4-{[(2S,3S,4S,5R)-5-{(1E)-N-[(3-chloro-2,6-difluorobenzyl)oxy]ethanimidoyl}-3,4-dihydroxytetrahydrofuran-2-yl]oxy}-3-hydroxyphenyl)-2-methyl-N-[(3aS,4R,5R,6S,7R,7aR)-4,6,7-trihydroxyhexahydro-1,3-benzodioxol-5-yl]prop-2-enamide: m/z 688 → 366 negative ion mode and m/z 686 → 366 positive ion mode).
In Vitro Data Analysis.
The modeling approach used to analyze the SCHH data was analogous to the method described previously for suspended and plated hepatocytes by Paine et al. (2008) and Poirier et al. (2008), respectively. To address biliary excretion, additional model terms have been proposed for the analysis of extended incubation times (Lee et al., 2010); however, these parameters cannot be estimated with the duration of experiment used here.
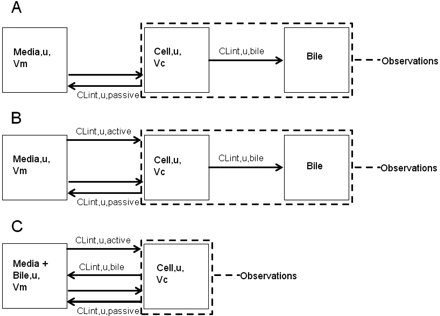
The model includes compartments representing the media, cell, and bile environments of the experiment, with passive diffusion, active uptake, and efflux processes incorporated in a mechanistic fashion, as illustrated in Fig. 2. The passive diffusion component was parameterized as unbound distribution CL (CLint, u, pass) within the model. Active uptake was parameterized in the form of unbound uptake CL (CLint, u, act). Two further clearance mechanisms were incorporated, namely, unbound biliary CL (CLint, u, bile) and unbound metabolic CL (CLint, u, met). Efflux transport by sinusoidal transporters was assumed to be negligible. There are studies to suggest bidirectional transport by OATPs, but these are generally based on oocyte data (Mahagita et al., 2007) and have not been considered here. It was assumed that only unbound drug is able to pass across the cell membrane and that any binding to the cell membrane is instantaneous. Equations 1, 2, and 3 are used in this modeling process:
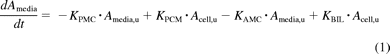
where KPMC is CLint, u, pass/Vm, Vm is media volume (microliters), u represents unbound, KPCM is CLint, u, pass/Vc, Vc is cell volume (microliters), KAMC is CLint, u, act/Vm, KMET is CLint, u, met/Vc, KBIL is CLint, u, bile/Vc, Amedia is the amount in media (picomoles), Acell is the amount in cell (picomoles), Abile is the amount in bile (picomoles), cell,u is cell × fu,cell, and media,u is media × fu, media.
Intrinsic clearance (CLint) units are microliters per minute per million cells (Mcells), and it was assumed on the basis of in-house data that 1 Mcells is equivalent to 1 mg of protein. The volume of the whole incubation (Vinc) is the sum of the medium and cell volumes, Vm and Vc, respectively. Vc was estimated by assuming that 1 Mcells is equivalent to 4 μl (Reinoso et al., 2001). The fraction unbound in the media (fu, media) was assumed to equal 1, because no protein was present. The fraction unbound in the hepatocyte (fu, cell) was calculated using a rearranged form of the equation reported by Poulin and Theil (2000) (eq. 4), assuming that the concentration of albumin in liver relative to that in plasma (Cm, tissue) is equal to 0.5. This parameter accounts for nonspecific binding of the drug intracellularly within the hepatocyte and was fixed in further modeling of in vitro data:
where fu, p is the fraction unbound in the plasma.
Nonzero initial conditions were set for the cell and media compartments to account for instantaneous nonspecific binding to cells and/or experimental apparatus. This amount was calculated from Vm, Vc, and the binding constant (KB) as described in the literature (Paine et al., 2008; Poirier et al., 2008) (eqs. 5 and 6):
When significant metabolism was observed, CLint, u, met was set to the unbound CLint value determined in human liver microsomes (HLM), adjusted from microliter per minute per milligram to microliter per minute per Mcells using the ratio of hepatocellularity to microsomal recovery (HLM CLint, u × microsomal recovery/hepatocellularity). The model fitting of CLint, u, pass, CLint, u, act, CLint, u, bile, and KB was performed in NONMEM (version VI level 1.2), in NM-TRAN subroutines (version III level 1.2, 2006; Icon Development Solutions, Ellicott City, MD), or in acslX (version 3.0.1.6; Aegis Technologies, Huntsville, AL). The HYBRID estimation method in NONMEM was used, and first-order estimation was used to estimate all the parameters. Residual error was estimated using a proportional error model.
In Vivo Simulations.
An intravenous PBPK model was used to model the in vivo situation. The PBPK model was composed of 15 compartments corresponding to the different tissues of the body, namely, adipose tissue, bone, brain, gut, heart, kidney, liver, lung, muscle, skin, spleen, testes, and rest of body, which were connected by the circulating blood system (arterial and venous). Each compartment was defined by a tissue volume and a tissue blood flow rate; these physiological parameters for humans have been described elsewhere (Jones et al., 2006). Each tissue was assumed to be perfusion rate-limited, with the exception of liver. The liver and kidney were considered to be the only sites of elimination.
The mass balance differential equations (except for liver) used in the model have been described previously (Jones et al., 2006, 2011) and follow the principles shown in eqs. 7 and 8:
where Q is blood flow (liters per hour), C is concentration (milligrams per liter); V is volume (liters), T is tissues, a is arterial, v is venous, CvT represents CT/Kp · B/P, Kp is the tissue to plasma partition coefficient of the compound, and B/P is the blood/plasma ratio.
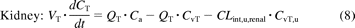where CLint, u, renal is the unbound renal intrinsic clearance of the compound (liters per hour). CLint, u, renal was calculated from the renal CL reported from the respective clinical study, assuming well-stirred conditions (Supplemental Table S1).
The Kp values (for all tissues except for the liver) were estimated using tissue composition equations developed in the literature (Rodgers and Rowland, 2006). The tissue composition parameters reported by the authors were used. The main compound-specific parameters required were log D7.4, pKa, B/P ratio, and fu, p. These predictive equations account for four main processes: 1) partitioning of un-ionized drug into neutral lipids and neutral phospholipids; 2) dissolution of ionized and un-ionized drug in tissue water; 3) electrostatic interactions between ionized drug and acidic phospholipids for strong ionized bases; and 4) interactions with extracellular protein for neutral compounds, weak bases, and acids. These equations assume only passive distribution and do not account for any active transport processes. Tissue composition data and anatomical information were available for each tissue in the model. It was desirable to include the full PBPK model to get initial estimates of exposure related to safety concerns and to provide a framework for elaboration of transporters in other tissues.
The liver was modeled as a permeability-limited tissue, incorporating scaled active uptake (SCLint, u, act) and scaled passive diffusion clearances (SCLint, u, pass) of unbound drug at the sinusoidal membrane, scaled biliary clearance (SCLint, u, bile) of unbound drug at the canalicular membrane, and scaled metabolic clearance (SCLint, u, met) of unbound drug (where appropriate). These scaled parameters (liters per hour) were calculated from the in vitro parameters CLint, u, act, CLint, u, pass, CLint, u, bile, and CLint, u, met obtained in SCHH, accounting for the hepatocellularity and liver weight as described previously (Houston, 1994). The liver compartment was subdivided into five units of extracellular and intracellular compartments, connected by blood flow in tandem (Watanabe et al., 2009), as shown in Fig. 2. Watanabe et al. reported that for pravastatin, five sequential compartments most closely approximated the partial differential equation dispersion model, so this number of compartments was retained. Initial modeling (results not shown) used one liver tissue and liver blood. The corresponding differential equations used (eqs. 9–11) are shown below:
where CEC is extracellular concentration (milligrams per liter), CIC is intracellular concentration (milligrams per liter), VEC is the volume of extracellular compartment (liters), VIC is volume of the intracellular compartment (liters), ha is hepatic artery, gu is gut, sp is spleen, and li is liver.
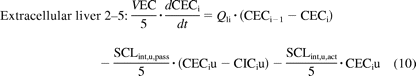
The model simulations were performed in Berkeley Madonna (version 8.3.9, 1996–2006; University of California, Berkeley, CA). Maximal contribution of the active process to the total uptake was estimated and is expressed as the ratio of CLint, u, act and total uptake CLint (CLint, u, act + CLint, u, pass).
In Vivo-Fitting.
In addition to the simulations, a fitting procedure was performed. With use of the observed clinical intravenous data (extracted via DigitizeIt, version 1.5.7), the SCLint, u, act, SCLint, u, pass, and SCLint, u, bile were estimated by the PBPK model, assuming that all other parameters within the model were correct and using the scaled parameter values as the initial estimates. For cerivastatin, bosentan, and fluvastatin for which metabolic and biliary clearance data were available, the sum of SCLint, u, bile and SCLint, u, met was fitted because SCLint, u, bile could not be uniquely identified. For repaglinide, SCLint, u, bile was assumed to be negligible and the predicted SCLint, u, met was fixed. The fitting procedure was performed using a proportional error model implemented within Berkeley Madonna by log transformation of the data. For the individual compounds, empirical scaling factors were calculated for each of these parameters by dividing the measured (scaled to intact liver) value by the fitted value.
The geometric mean of the empirical scaling factors across the drugs in the dataset was calculated. The intravenous PK for each compound was further simulated using the in vitro data together with the average empirical scaling factors within the PBPK model. The simulations were compared graphically with the observed clinical data. The predicted PK profiles with and without average empirical scaling factors were modeled in WinNonlin (version 5.2; Pharsight, Mountain View, CA) using noncompartmental analysis to determine volume of distribution at steady state (Vss) and CL parameters.
Local Sensitivity Analyses.
Local sensitivity analyses were conducted in acslX for each of the seven compounds to obtain numerical estimates of the partial derivative of the model with respect to each parameter. Each parameter was raised or lowered by 1% with respect to its value for that compound, and the value of the plasma concentration was obtained at three selected times throughout the time course during simulations of the conditions used for fitting in vivo parameters. Sensitivity coefficients were normalized to both the parameter value and the model output value, so when the output changes by 1% for a 1% change in the input parameters, the sensitivity coefficient is 1 or −1, depending on the direction of change. Only parameters with normalized sensitivity coefficients greater than 0.3 or less than −0.3 are reported.
Results
Physicochemical Properties.
A summary of the available in vitro data (excluding hepatic uptake data) and physicochemical properties for pravastatin, cerivastatin, bosentan, fluvastatin, rosuvastatin, valsartan, and repaglinide is shown in Table 1. All compounds were acidic. The log D7.4 measurements ranged from very hydrophilic at −0.88 for valsartan to lipophilic at 2.1 for repaglinide. B/P ratios were comparable across compounds, ranging from 0.48 to 0.76. For cerivastatin, bosentan, fluvastatin, valsartan, and repaglinide, fu, p values were very low (<1%), whereas fu, p values for rosuvastatin and pravastatin were higher at 9.4 and 43%, respectively. HLM CLint values were determined via substrate depletion experiments and corrected for nonspecific binding. Pravastatin, rosuvastatin, and valsartan had no measurable metabolism in HLM, whereas CLint, u, met ranged from 22 to 128 μl · min−1 · mg−1 for the remaining compounds (Table 1).
Physicochemical and in vitro properties for the compounds studied
Clinical Data.
The corresponding human PK parameters for each compound are reported in Supplemental Table S1. These data were obtained from intravenous PK studies reported in the literature (see References in supplemental data). CL ranged from 0.49 to 14 ml · min−1 · mg−1 for valsartan and pravastatin, respectively, whereas Vss covered a 10-fold range with fluvastatin and rosuvastatin at the low and high ends, respectively. Pravastatin, rosuvastatin, and valsartan exhibited a 29 to 47% contribution of renal excretion to their total CL.
In Vitro Data SCHH Analysis.
The in vitro SCHH data obtained for all seven drugs investigated are shown in Supplemental Figure S1. The SCHH data were simultaneously modeled as described under Materials and Methods section and in Fig. 1. The derived parameter estimates of CLint, u, act, CLint, u, pass, and CLint, u, bile are shown in Table 2. This assay was performed in two donors (except bosentan) and on a number of occasions. For the purposes of modeling, fu, cell, which describes the free fraction in the cell and the fraction nonspecifically bound (i.e., 1 − fu, cell), was fixed to the value predicted using eq. 4. Within the fitting process, sinusoidal efflux was assumed to be negligible. The parameter values were estimated to an acceptable precision level, and diagnostic plots and visual inspection of the observed versus fitted data indicated a good model fit (plots not shown). A 60-fold range in total uptake CLint values was observed, with pravastatin showing the lowest total uptake CLint (less than 2 μl · min−1 · Mcells−1) and repaglinide the highest (119 μl · min−1 · Mcells−1). Despite this, the maximal contribution of active processes to uptake CLint varied and was not necessarily correlated with the total uptake CLint. Pravastatin and valsartan both exhibited low uptake into the hepatocyte; however, the maximal active contribution was proportionally high at 95 and 78%, respectively. In contrast, the total uptakes of fluvastatin and repaglinide were much higher, with maximal active contributions of 69 and 25%, respectively; for these compounds, the contribution of passive diffusion was substantial and also subject to variability in the case of repaglinide. Bosentan, cerivastatin, and rosuvastatin exhibited intermediate uptake with a range of maximal active uptake contribution of 65, 28, and 85%, respectively. CLint, u, bile of the parent compound varied for the different compounds from 0 in the case of repaglinide to 96 μl · min−1 · Mcells−1 for valsartan. For all these compounds, uptake CLint (passive and active) determined in suspended hepatocytes was within 2- to 3-fold of the SCHH data (data not shown).
Schematic diagram of the in vitro model. A, conditions: 0.1 mM rifamycin SV. B, conditions: HBSS. C, conditions: Ca2+/Mg2+-free, 1 mM EGTA.
In vitro parameters estimated from sandwich culture human hepatocyte parameters at a single substrate concentration
Data represent mean from multiple replicates in one to two donors (S.D., where replicates are >2).
In Vivo Simulations and Fitting.
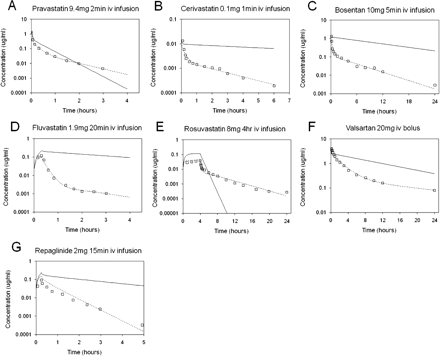
The in vitro parameters derived from the simultaneous modeling of the SCHH data and the HLM CLint, u, met were scaled to the in vivo situation to account for hepatocellularity, microsomal recovery, and liver weight. Scaled SCLint, u, act, SCLint, u, pass, SCLint, u, bile, and SCLint, u, met parameters are shown in Table 3 for all the drugs investigated. The Kp values, fu, p, fu, cell, and B/P ratio as well as SCLint, u, active, SCLint, u, passive, SCLint, u, bile, and SCLint, u, met were input into the whole-body PBPK model described under Materials and Methods and in Fig. 2. The clinical dose was simulated for each compound using the whole-body PBPK model. The simulated versus observed profiles for each compound are shown in Fig. 3. The simulation overpredicted exposure compared with the observed data, except for pravastatin and rosuvastatin, suggesting underestimation of the initial distribution phase.
In vitro scaled and fitted sandwich culture human hepatocyte estimates
Schematic diagram of the in vivo PBPK model. EC, extracellular; IC, intracellular.
Simulated, fitted, and observed human intravenous plasma concentration-time profiles for pravastatin (A), cerivastatin (B), bosentan (C), fluvastatin (D), rosuvastatin (E), valsartan (F), and repaglinide (G). □, observed data; ——, predicted data using the PBPK model; – – –, fitted data.
To rationalize the misestimation of the observed human intravenous plasma concentration time profile, the SCLint, u, active, SCLint, u, pass, and SCLint, u, bile were estimated using the model and the observed clinical intravenous data, assuming that all other parameters within the model were correct. These fitted parameters are shown in Table 3, and the profiles originating from these fitted parameters are shown in Fig. 3, in parallel to the initial simulations. As can be seen in Fig. 3, the fit for each compound accurately describes the observed plasma concentration-time data and corresponds to the shape of the observed profile. Goodness-of-fit plots are shown in Supplemental Figure S2. The fitted parameters were compared with the predicted parameters for each drug to generate an empirical scaling factor. The in vivo-fitted SCLint, u, act was significantly (p < 0.0001) higher than the in vitro-scaled value for the entire dataset, with empirical scaling factors ranging from 12 to 161 for rosuvastatin and fluvastatin, respectively, resulting in a geometric mean empirical scaling factor of 58. Consistent with expectations for a model approximating the liver acinar gradient (five sequential subcompartments) versus a single tissue and blood compartment, initial modeling with the single unit model required higher empirical scaling factors for fluvastatin and other compounds with high active uptake. In contrast, values were more comparable between the two models for rosuvastatin and compounds with slower uptake rates, with a geometric mean empirical scaling factor of 95 (results not shown). In the majority of cases, the in vivo-fitted and in vitro-scaled SCLint, u, pass compared well with each other giving a geometric mean scaling factor of 1. The only exception was valsartan for which scaling of passive permeability was required to fit the terminal phase of the profile. For each of the seven compounds, the in vivo-fitted SCLint, u, bile was on average 16-fold lower than the in vitro-scaled value, giving empirical scaling factors less than 1 (Table 3). For cerivastatin, bosentan, and fluvastatin, the empirical scaling factors for SCLint, u, bile could not be estimated because these compounds also undergo measurable P450 metabolism, and the model could not uniquely identify these two parameters. For this reason, the two parameters were summed and fitted together. For repaglinide, there was no measurable CLint, u, bile. The empirical scaling factor for SCLint, u, bile (0.061) was therefore calculated using only three compounds (pravastatin, rosuvastatin, and valsartan).
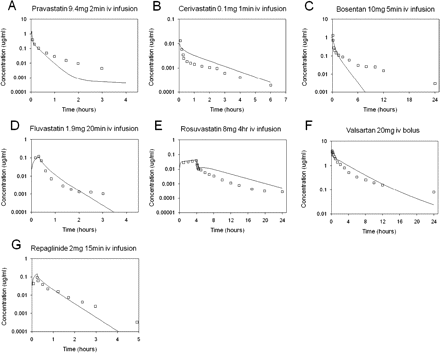
These average empirical scaling factors for active uptake and biliary efflux were subsequently reapplied to the seven compounds to resimulate the clinical intravenous data. Figure 4 shows simulated plasma concentration-time profiles based on the SCHH estimates for SCLint, u, act, SCLint, u, pass, and SCLint, u, bile scaled by the average empirical scaling factors of 58, 1, and 0.061 for the corresponding processes, respectively; all other parameter inputs were as used for simulations shown in Fig. 3. Use of average empirical scaling factors, compared with simulations performed without them, resulted in better agreement between the simulated profile and observed data for the majority of the compounds. The biphasic profile for bosentan was not accurately captured using the generic empirical scaling factor; the fitting procedure reduced combined metabolism and biliary efflux to a value lower than SCLint, u, met (55 versus 87 l/h) (Table 3), whereas for the resimulation the in vitro metabolism-scaled value was used.
Simulated (using the average empirical scaling factor for individual processes) and observed human intravenous plasma concentration-time profiles for pravastatin (A), cerivastatin (B), bosentan (C), fluvastatin (D), rosuvastatin (E), valsartan (F), and repaglinide (G). □, observed data; ——, predicted data using the PBPK model. The average empirical scaling factors are listed in Table 3.
The predicted Vss and CL parameters using different modeling scenarios are shown in Table 4. For each compound, both the CL and Vss were underpredicted when the in vitro data alone were used in the PBPK model with an absolute average fold error of 7.1 and 3.0, respectively. However, when these data were corrected for the average empirical scaling factors, the predicted CL and Vss parameters corresponded more accurately with the observed data with absolute average fold errors of 1.3 and 1.7, respectively.
Predicted CL and Vss parameters for the seven drugs investigated using different modeling scenarios
Local Sensitivity Analyses.
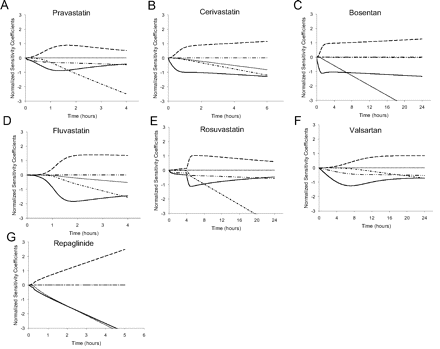
For each of the seven compounds, all parameters were investigated to assess their sensitivity to the model simulation of the plasma concentration profile. This analysis included all the physiological parameters in the model as well as those specific for each compound. Very few of the physiological parameters had normalized sensitivity coefficients greater than 0.3 or less than −0.3, indicating very limited impact when these parameters were varied individually (data not shown). Physiological parameters to which multiple compounds were sensitive included body weight, cardiac output, volume of liver tissue, and liver blood flow. The fu, p, fu, cell, B/P ratio, SCLint, u, act, and SCLint, u, pass were sensitive parameters, along with SCLint, u, bile, SCLint, u, met, and CLint, u, renal, as appropriate to each compound. The sensitive parameters showed complex changes as would be expected for the different exposure regimens and varying importance of processes throughout the duration of the observed plasma time course. Figure 5 illustrates that the early plasma time course is increasingly sensitive to liver uptake (with SCLint, u, act and SCLint, u, pass having opposite impacts), whereas the later time course becomes increasingly sensitive to the clearance from the liver (SCLint, u, bile and SCLint, u, met) and CLint, u, renal.
Time-dependent sensitivity analysis of the importance of CLint, u, act, CLint, u, pass, CLint, u, met, and CLint, u, bile parameters on the plasma kinetics of pravastatin (A), cerivastatin (B), bosentan (C), fluvastatin (D), rosuvastatin (E), valsartan (F), and repaglinide (G). ——, CLint, u, act; – – –, CLint, u, pass; · · · · ·, CLint, u, met; — · —, CLint, u, bile; — · · —, renal CL.
Discussion
Prediction of human PK remains an important feature of drug discovery to help select compounds with appropriate characteristics for clinical development. Physiologically based methods for human PK prediction are reasonably well established for small lipophilic compounds cleared by liver metabolism (Jones et al., 2006, 2011; De Buck et al., 2007; Rostami-Hodjegan and Tucker, 2007) and have recently been applied for a better understanding of intestinal first-pass metabolism (Gertz et al., 2010). However, the optimization of compound properties to improve metabolic stability has led to a reduction in lipophilicity and permeability and hence a shift in CL routes from liver metabolism to transporter-mediated uptake and efflux. The prediction of such processes in humans continues to be a challenge (Liu and Pang, 2006; Poirier et al., 2009a; Watanabe et al., 2009).
Using a SCHH in vitro system together with available clinical plasma concentration-time data for seven compounds, we have established a prediction approach for active liver uptake and efflux. These SCHH in vitro data were dynamically modeled as outlined in Fig. 1. In contrast to previous modeling efforts (Paine et al., 2008; Poirier et al., 2008), the current model allowed estimation of biliary efflux and active and passive uptake from the same in vitro experiment through modulation of calcium ions (Liu et al., 1999; Bi et al., 2006; Lee et al., 2010; Yan et al., 2011). The in vitro mechanistic model was parameterized in such a way to separate out the intracellular binding and the active processes; hence, the fu, cell term was fixed to the predicted value. An accurate estimation of this parameter is particularly important to estimate the free concentration in the liver and influences the rate of metabolism/biliary excretion. Here, fu, cell was predicted using eq. 4; however, improved prediction approaches may be needed (Yabe et al., 2011). These in vitro parameters were then scaled to in vivo and were subsequently integrated into a whole-body PBPK model, together with other absorption, distribution, metabolism, and excretion properties to simulate the human plasma concentrations (Fig. 2). Prediction accuracy of these simulations was assessed by comparison with observed plasma concentration-time profiles reported in the literature. The simulations in Fig. 3 show that the plasma concentration time profiles were significantly overestimated, with the initial phase of the profile being significantly mispredicted, perhaps indicating an underprediction of the initial distribution into the liver, as observed by others (Poirier et al., 2009a; Watanabe et al., 2009). With use of a fitting procedure, the PBPK model together with the observed plasma concentration-time data was used to estimate the in vivo values for the SCLint, u, act, SCLint, u, pass, and SCLint, u, bile that would better describe the observed data. Table 3 shows the fitted values together with the empirical scaling factors describing the relationship between the fitted and measured parameters. In general, SCLint, u, act and SCLint, u, bile were underpredicted (58-fold) and overpredicted (16-fold), respectively; no empirical scaling factor was required for passive diffusion. The values for empirical scaling factors reported here are specific to our implementation of the SCHH; other laboratories would need to reestimate their own system-specific empirical scaling factors.
Previous studies have also reported the need for empirical scaling factors for active uptake for pravastatin and valsartan to recover the human plasma concentrations (Poirier et al., 2009a; Watanabe et al., 2009). The basis for this empirical scaling factor is unclear. An evaluation of OATP expression in SCHH showed that, although OATP1B3/OATP2B1 expression were reduced to ∼50% of that in suspension, OATP1B1 expression was increased to ∼150% (Supplemental Table S2). These results are consistent with recent studies that show no effect of the culture time on uptake transporter activity in SCHH for rosuvastatin (Kotani et al., 2011), which would not support the hypothesis that the expression of uptake transporters is down-regulated in this system. However, the difference between OATP expression in culture and in vivo is unknown. The model fitting was performed using plasma concentration-time data alone; the lack of liver concentration data to assist in model fitting may mean that the fitted values for SCLint, u, act, SCLint, u, pass, and SCLint, u, bile have not been estimated accurately, although this would be expected to have more impact on the biliary transport value than on the active uptake. However, the issue of parameter identifiability has been investigated, and the combination of parameters obtained by fitting appeared unique in their ability to accurately describe the plasma concentration-time profiles of these compounds (see contour plots in Supplemental Fig. S3), given the model structure used and the values of the other parameters. In addition, the fitting routine assumes that all other parameters within the PBPK model were correct and that all other tissues (excluding the liver) are perfusion rate-limited. However, expression of OATP transporters has been reported in other tissues, e.g., kidney (Hilgendorf et al., 2007), and this could partially explain the large empirical scaling factors required when liver alone is assumed to be the main transport organ. Initial data on transporter abundance are becoming available (Schaefer et al., 2012); however, until detailed transporter expression data are reported for the liver and other tissues, this will remain a caveat of this analysis. In terms of the passive uptake into the liver, the SCLint, u, pass scaled accurately from in vitro to in vivo, probably due to the lack of dependence on enzymatic or active processes that could be up- or down-regulated on culturing. This result has also been observed also by others in the literature for humans and rats (Paine et al., 2008; Poirier et al., 2009a,b; Watanabe et al., 2009).
One limitation of the modeling reported here is that it does not address enterohepatic recirculation for the drugs with substantial biliary excretion, as explicitly demonstrated with rosuvastatin in rats (Nezasa et al., 2002). The absence of recycling would mean that the estimated biliary efflux would represent only the net CL (i.e., excreted minus reabsorbed), resulting in the observed overprediction. A more complex model to describe the recycling of drug from bile back into the intestine is required to fully understand this empirical scaling factor and would facilitate incorporation of additional published human data for intraduodenal dosing and biliary excretion of rosuvastatin (Bergman et al., 2006). An evaluation of our SCHH assay indicated that these biliary efflux proteins are up-regulated by ∼3-fold during the 5-day culture period, which would also in part explain the overprediction observed (Bi et al., 2012).
The sensitivity analysis showed complex changes as would be expected for the different exposure regimens and varying importance of processes throughout the duration of the observed plasma time course, illustrating the value of fitting multiphasic intravenous plasma concentration-time data for estimation of the empirical scaling factors (to estimate misprediction) rather than relying solely on reported PK parameter values.
Although each compound showed the same trend in terms of empirical scaling factors, there was a high degree of variability in the derived values, suggesting that the de novo application of these parameters to novel compounds may be uncertain. This variability could result from several factors, e.g., multiple/different transporters between compounds and genetic polymorphisms for some transporters. The purpose of this analysis was to explore the utility of using SCHH data to simulate human transporter-mediated PK. Several issues have been identified that require further investigation. Availability of in vitro transporter data in a larger number of donors in conjunction with protein expression data is required to further improve transporter in vitro-in vivo extrapolation. However, Fig. 4 shows that the application of the average empirical scaling factors to these compounds gives a reasonable description of the plasma concentration-time profile. In addition, the application of these average empirical scaling factors results in a good prediction accuracy for CL and Vss parameters with absolute average fold errors of 1.3 and 1.7, respectively (Table 4). However, the true test for this prediction approach is its application to novel compounds. We have recently applied the average empirical scaling factors derived in this study for the seven literature compounds for simulation of the human PK of four novel OATP substrates entering a first-in-human study at Pfizer. The PBPK prediction methodology resulted in better prediction accuracy compared with that for other allometric scaling and more traditional in vitro-scaling approaches (data not shown). In our study, we used the observed renal CL values determined from the clinical data. However, when simulations for novel compounds are conducted, this parameter would need to be predicted from preclinical data.
In summary, this study has provided a systematic analysis of seven transporter substrates in SCHH. A mechanistic prediction methodology has been proposed for scaling of human PK for the compounds investigated using data generated in SCHH. Although this approach relies on the use of empirical scaling factors for active uptake and biliary efflux, it allows simultaneous assessment of multiple processes occurring in the hepatocytes in a mechanistic manner and improves our understanding of the relevance of these processes for hepatic disposition of drugs. Further understanding of the necessity for these empirical scaling factors is required to increase confidence in the applicability of this methodology to novel compounds.
Authorship Contributions
Participated in research design: Jones, Barton, Lai, El-Kattan, and Fenner.
Conducted experiments: Lai, Bi, Kimoto, Kempshall, Tate, and Fenner.
Performed data analysis: Jones, Barton, and Tate.
Wrote or contributed to the writing of the manuscript: Jones, Barton, Lai, Bi, Kimoto, Kempshall, Tate, El-Kattan, Houston, Galetin, and Fenner.
Acknowledgments
The assistance of scientists at the Hamner Institutes for Health Sciences (Research Triangle Park, NC), including Jerry Campbell and Alina Efremenko, in converting the code to acslX software and carrying out initial local sensitivity analyses is greatly appreciated.
Footnotes
Article, publication date, and citation information can be found at http://dmd.aspetjournals.org.
↵
The online version of this article (available at http://dmd.aspetjournals.org) contains supplemental material.ABBREVIATIONS:
- PK
- pharmacokinetic(s)
- PBPK
- physiologically based pharmacokinetic
- CL
- clearance
- OATP
- organic anion-transporting polypeptide
- SCHH
- sandwich culture human hepatocytes
- HBSS
- Hanks' balanced salt solution
- HLM
- human liver microsomes
- B/P
- blood/plasma ratio
- Mcells
- million cells.
- Received September 23, 2011.
- Accepted February 16, 2012.
- Copyright © 2012 by The American Society for Pharmacology and Experimental Therapeutics
